ЗОЛОТОЕ СЕЧЕНИЕ И ЗОЛОТЫЕ ПРЯМОУГОЛЬНИКИ ПРИ ПОСТРОЕНИИ ИКОСАЭДРА И ДОДЕКАЭДРА

(Южно-уральский государственный университет (Национальный Исследовательский Университет))

Аннотация

В статье показано построение 3D модели додекаэдра при помощи прямоугольников с отношением сторон на основе золотого сечения (ЗС). Приведено построение двойственных фигур: икосаэдра и додекаэдра, вписанных в куб и описанных около него, а также их каскада с использованием прямоугольников со сторонами пропорции ЗС в AutoCAD.

Ключевые слова: золотое сечение, золотой прямоугольник, икосаэдр, додекаэдр, AutoCAD

1. Введение

Известны многочисленные способы построения правильных многогранников (ПМ) и наиболее сложных из них икосаэдра и додекаэдра. Среди них особый интерес вызвал способ построения икосаэдра на основе золотых прямоугольников (ЗП) с отношением сторон золотого сечения (отношение целого к большей части). Этот способ, отличающийся простотой, изящностью и внутренней гармонией, по нашему мнению, изучен недостаточно, т.к. не распространен на додекаэдр, который строится, как фигура двойственная икосаэдру.

Цель работы: Дополнить способ построения при помощи прямоугольников с отношением сторон на основе ЗС для додекаэдра.

Построение выполнялись в пакете AutoCAD [1], но могут быть повторены и в других известных САПР.

2. История

Считается, что свое «становление» правильные многоугольники (ПМ) получили в VI веке до н.э. в самой известной Пифагорейской философской школе древней Греции, где царила идея, что Вселенная подчинена закону гармонии, который можно выразить в числах. Пифагору Самосскому и его ученикам принадлежат первые открытия в геометрии, им были известны тетраэдр, куб, октаэдр и ЗС. Додекаэдр и икосаэдр первым описал Теэтет Афинский, он же дал математическое описание правильных многогранников и доказательство того, что их только пять [2, 3].

Платон, разделявший взгляды пифагорейцев на гармонию мироздания, в трактате «Тимей» развил учение о пропорциях и сопоставил правильные многогранники четырем «стихиям» природы. Так геометрические представители числовой гармонии Вселенной получили название Платоновых тел.

В III в. до н. э. итогом развития древнегреческой науки стала книга «Начала» Евклида, где во II книге дано геометрическое построение «золотого» деления, а в заключительной XIII книге приведено строгое построение всех правильных тел. Гипсикл Александрийский считается автором дополнительной XIV книги «Начала», в которой приводятся свойства икосаэдра и додекаэдра, вписанных в одну и ту же сферу.

В эпоху Возрождения при создании изобразительной геометрии и теории перспективы «впервые со времен Эвклида был возобновлен разговор о ЗС, Платоновых телах и ПМ» [4]. Этот период связан с именами таких великих личностей, как Ф. Брунеллески, Пьеро делла Франческа, Лука Пачоли, Леонардо да Винчи, А. Дюрер, И. Кеплер.

Теория многогранников тесно связана с новыми разделами математики: топологией, теорией графов, комбинаторикой многогранников и имеет большое значение для практических приложений в других разделах математики (алгебре, теории чисел, прикладной математике), а также в физике, кристаллографии. Научные мысли в этих областях связаны с именами: Л. Эйлера, О. Коши, Л. Шлефли, Е. С. Фёдорова, Д. Ги́льберта, Кон-Фоссена, Ж. Адамара, Г. С. М. Кокстера, А.Д. Александрова, В. Г. Ашкинузе и др.

Пяткрка ПМ не теряет популярность на протяжении всей истории науки. И в наши дни на основе Платоновых тел и ЗС были сделаны «выдающиеся научные открытия современной науки, … в частности, квазикристаллы и фуллерены, удостоенные Нобелевских премий» [5].

ПМ изучают в школьном курсе геометрии [6], в основе которого до сих пор лежат «Начала» Эвклида. В курсе начертательной геометрии к ПМ обращаются изредка [7], несмотря на содержательный предмет исследования и наличие интересных свойств.

3. Основные понятия

Правильный многогранник – это выпуклый многогранник, каждая грань которого правильный p-угольник и в каждой ее вершине сходится одинаковое число q таких граней.

Рассмотрим икосаэдр и додекаэдр, как наиболее сложные и интересные среди тел Платона не только множеством симметрий, но и наличием в их геометрии правильных пятиугольников и, как следствие, пропорций ЗС.

ПМ принято обозначать символом Шлефли {р, q}: икосаэдр {3, 5} и додекаэдр {5, 3}. Они подчиняются формуле Эйлера, связывающей число вершин (В), граней (Г) и рёбер (Р) любого выпуклого многогранника простым соотношением: В + Г = Р + 2.

Эта пара двойственных (дуальных) фигур, что проявляется при построении, они меняют не только положение вершин и центров граней относительно друг друга, но их количество. «Сделать им это легко», т.к. число граней Г=20 икосаэдра совпадает с числом вершин В=20 додекаэдра, а число вершин В=12 икосаэдра равно числу граней Г=12 додекаэдра. У них одинаковое количество ребер Р=30. Оба многогранника имеют по 1 центру симметрии и по 15 осей и плоскостей симметрии. И символы Шлефли {3, 5} и {5, 3} у них зеркальны.

Это дает основание предположить, что для двойственных фигур способы построения должны быть аналогичные.

4. Построение икосаэдра и додекаэдра

Последователем древних греков в изучении тел Платона был итальянский математик, ученый монах Лука Пачоли. В книге «О божественной пропорции» [8, 9], проиллюстрированной Леонардо да Винчи, он представил ЗС и ПМ в соответствии с XIV книгой «Начал» [4]. Здесь же он впервые называет «непостижимым» тот эффект, что «сторона куба и сторона треугольника твердого тела из 20 граней, когда оба ограничены одной и той же сферой», соответствуют пропорции ЗС [8]. Это означает, что икосаэдр можно построить с помощью ЗП. Такие ЗП были известны и до публикации Л. Пачоли, свидетельство тому Парфенон в Афинах [10].

Алгоритм построения икосаэдра на основе ЗП следующий: «вставляется один в другой три равных ЗП перпендикулярно друг другу по срединной параллели, остается только соединить ближайшие друг к другу вершины. Чтобы построить додекаэдр, нужно соединить центры граней икосаэдра. Великолепный пример ясности рассуждений!» [11].

Существует много способов построения ПМ [8, 12-15]: можно их вписать в сферу или описать около нее; использовать последовательное каскадное вписывание-описывание относительно друг друга (число возможных каскадов равно 5!=120 [12]); построить фигуры на основе куба (например, додекаэдр способом «крыш», предложенным Евклидом); с использованием пропорций ЗС; с применением формул или только на основе геометрических построений и др. Можно создать плоское изображение или объемную модель на компьютере [16].

Возникает вопрос: почему в источниках [8, 9, 12-15, 17], где речь идет о ЗП для построения икосаэдра, нет упоминания об аналогичном способе для додекаэдра? Да, прямоугольники для додекаэдра будут не «чисто» золотые (отношение сторон, как целого к меньшей части), но из «семейства» ЗС и какие наглядные.

И. Кеплер называл куб «родителем» всех ПМ может потому, что на его основе все другие создаются наиболее рационально, логично и наглядно. Рассмотрим построение 3D моделей икосаэдра и додекаэдра в AutoCAD на основе прямоугольников пропорции ЗС, у которых большая сторона а будет равна стороне условного куба. Следовательно, фигуры можно рассматривать как вписанные в куб.

5. Построение икосаэдра, вписанного в куб

Вначале построим икосаэдр по известному алгоритму.

Стороны прямоугольника H (рис. 1, а) должны находиться в отношении ЗС. Методом треугольника (рис. 1, б) делим отрезок а на части такие, что a:c=c:b=Ф. Затем три одинаковых ЗП располагают симметрично и перпендикулярно друг другу. По алгоритму точки 1, 2, 3 (рис. 1, а) задают одну из 20 граней икосаэдра. В этой плоскости командой Правильный многоугольник / Сторона создаем треугольник с указанием т. 1 и 2, превращаем его в поверхность. Круговым массивом относительно точки 3 оси О-3 строим 5 граней с общей вершиной (см. рис. 1, в). К некоторым из граней трижды применяем команду 3D-зеркало, в качестве зеркальных плоскостей используем два ЗП и плоскость симметрии, заданую точками 4, 5, 6.

Применив команду Редактировать поверхность / Наполнить, преобразуем поверхности граней, образующих замкнутый объем, в 3D-тело (см. рис. 1, г). Икосаэдр готов.

6. Построение додекаэдра, вписанного в куб

Строим додекаэдр, используя для сравнения прежние ЗП с поправкой (можно построить новые). При построении выявляется интересная особенность. Оказывается, если икосаэдр и додекаэдр вписаны в один и тот же куб, то их стороны тоже находятся в золотом отношении Ф. Следовательно, сторона додекаэдра равна b – меньшему отрезку ЗС (см. рис.1, б). Вносим поправку в геометрию прямоугольников для додекаэдра, расположив отрезки b посередине малых сторон тех же ЗП (рис. 2, а). Отношение сторон (целого к меньшей части) нового прямоугольника для додекаэдра a:b≈2,618, а для икосаэдра у ЗП оно было a:c≈1,618.

В данном случае конечные точки 1, 2, 3 отрезков b укажут плоскость грани додекаэдра, в которой нужно вычертить Правильный пятиугольник / Сторона, указав точки 1 и 2. Диагональ пятиугольной грани равна стороне икосаэдра с.

Последующие действия команды Кругового массива с центром в точке В луча О-В (см. рис. 2, б) и трижды примененной 3D-зеркало относительно плоскостей прямоугольников создают замкнутый объем додекаэдра, ограниченный поверхностями. Создадим из него 3D тело – додекаэдр (рис. 2, в).

Итак, если фигуры вписаны в куб, то икосаэдр строится на основе прямоугольников со сторонами, в отношении целого и большей части, а додекаэдр – в отношении целого и меньшей части, где целое – это сторона куба.

7. Построение каскада двойственные фигур

Двойственные фигуры были построены на совпадающих ребрах с и b. Повернув додекаэдр (или икосаэдр) на 90°, создадим классическое двойственное соединение дуальных многогранников (рис. 3, а). Внешние вершины образуют выпуклую оболочку, называемую «ромботриаконтаэдром», а общая часть соединения – ядро носит название «икосододекаэдр».

Каркасное изображение этого двойственного соединения на виде по стрелке (см. рис. 3, а) показано на рис. 3, б. На нем наглядно видна конструкция двух ЗП со сторонами a, c и отрезком b, а также все элементы фигур: стороны – отрезки с и b; проецирующие грани икосаэдра – i и додекаэдра – d; положение их вершин – точки 1 и 2 – все, что необходимо для построения каскада дуальных многогранников.

Аналогичную 2D схему (ее верхнюю правую четверть – см. рис. 3, в) с изображением на ней центра симметрии т. О, граней икосаэдра i и додекаэдра d, а также положения их вершин т. 1 и 2 легко построить, т.к. все размеры известны из пропорции ЗС. На основе дуальности фигур нужно скопировать отрезки i и d к точкам 3, 4 и т.д., смоделировав этот бесконечный каскад на плоскости, и определить стороны ЗП для построения фигур в объеме.

Так, для «случайного» икосаэдра i' с вершиной в точке 6 отношение сторон его прямоугольника будет равно a':с'. Для додекаэдра d' с вершиной в точке 5 – a'':b'.

На рис. 3, г видим каскадное соединение дуалов, состоящее из 3 икосаэдров и 2 додекаэдров, с соответствием цвета фигур в объеме и на схеме.

8. Построение икосаэдр и додекаэдр, описанных около куба

На основе ЗП можно построить икосаэдр и додекаэдр, описанные около куба.

Чертим схему аналогичную рис. 3, б и добавляем контур куба со стороной а. На схеме (рис. 4, а) индекс v означает фигуры, вписанные в куб, o – описанные. Вначале строим додекаэдр d_о, используя т. 1– вершину куба (вершина куба соответствует вершине додекаэдра, но не очерковой, что хорошо видно на объемных фигурах), определяем стороны его прямоугольников – a_do и b_o. Полученная т. 2 на луче вершин икосаэдра, позволяет построить описанный икосаэдр i_o и определить стороны его ЗП – a_ioиc_o.

Изображение описанных даульных фигур около куба показано на рис. 3, б, в.

Определить стороны a_do и b_o ЗП додекаэдра, описанного около куба, можно также методом квадрата (см. рис. 4, г), т.е. находим приращение b_o в пропорции ЗС относительно a.

9. Выводы

Дополнен алгоритм построения додекаэдра применением трех взаимно перпендикулярных прямоугольников со сторонами пропорции ЗС.

Показано, что этот алгоритм позволяет наглядно и просто строить не только один из представителей «высшего порядка» тел Платона – икосаэдр, но и додекаэдр.

Установлено, что прямоугольники с отношением сторон пропорции ЗС можно использовать при построении фигур как вписанных в куб, так и описанных около него.

Схема, созданная на основе ЗП, позволяет «предвидеть» каскад двойственных икосаэдра и додекаэдра и определить размеры ЗП для его построения.

Про прямоугольники с отношением сторон пропорции ЗС можно сказать, что они являют собой не только «великолепный пример ясности рассуждений», но и пример ясности представления. Впрочем, одно с другим связано.

Список литературы

Инженерная 3D-компьютерная графика: учебник и практикум для академического бакалавриата / А.Л. Хейфец, А.Н. Логиновский, И.В. Буторина, В Н. Васильева; под ред. А.Л. Хейфеца. – 3-е изд., перераб. и доп. – М.: Изд-во Юрайт, 2015. –602 с.
Шаль М. Исторический обзор происхождения и развития геометрических методов. Т. 2. Гл.1 § 1-8 – М.: Моск. мат. о-во, 1883. – 748 c. http://bookre.org/reader?file=444142&pg=2
Кольман Э. История математики в древности. М.: Государственное издательство физико-математической литературы, 1961. – 235 с. http://www.mathedu.ru/lib/books/kolman_istoriya_matematiki_v_drevnosti_1961/
Мартыненко Г.Я. Математика Гармонии: Возрождение (XIV–XVI вв.) (к 500–летию книги Луки Пачоли «О божественной пропорции») // Академия тринитаризма, (эл № 77-6567, публ.16006, 20.07.2010). http://www.trinitas.ru/rus/doc/0016/001c/1679-mrt.pdf
Стахов А.П. Математика гармонии: Инновации в информационных технологиях, в основаниях математики, в образовании. // Интернет-журнал Науковедение. М.: ИГУПИТ, №4, 2012. – С. 98. https://naukovedenie.ru/PDF/33tvn412.pdf
Крайнева Л.Б. Методика проведения спецкурса по геометрии для старшеклассников в условиях личностно-ориентированного обучения: дис. …канд. пед. наук. М., 2007. – 260 с. http://www.dissercat.com/content/metodika-provedeniya-spetskursa-po-geometrii-dlya-starsheklassnikov-v-usloviyakh-lichnostno-
Короев Ю.И. Начертательная геометрия. М.: КноРус, 2015. –422 с.
Divina proportione: opera a tutti glingegni... : Internet Archive [Электронный ресурс] https://archive.org/details/divinaproportion00paci/page/n41
Щетников А. И. Лука Пачоли и его трактат «О божественной пропорции» // Математическое образование, №1 (41), 2007. – С. 33–44. http://www.nsu.ru/classics/pythagoras/Pacioli.pdf
Ливио М. φ – Число Бога. Золотое сечение – формула мироздания: АТС, М., 2015. – 218 с. http://zodorov.ru/mario-livio---chislo-boga-zolotoe-sechenie--formula-mirozdaniy.html?page=7
Наука. Величайшие теории: выпуск 14: Трехмерный мир. Евклид. Геометрия. – М. Де Агостини, 2015. – 168 с. https://coollib.com/b/337501/read
Смирнова И.М. Каскады из правильных многогранников [Электронный ресурс] http://www.vasmirnov.ru/Lecture/Kaskady/Kaskady.htm
Гарднер М. Математические головоломки и развлечения: гл. 23 – М.: Мир, 1971. – 511 с. http://mathemlib.ru/books/item/f00/s00/z0000043/st025.shtml
Долбилин Н.П. Три теоремы о выпуклых многогранниках // Квант, №5, 6, 2001. –С.7-12. http://kvant.mccme.ru/pdf/2001/05/kv0501dolbilin.pdf
Долбилин Н.П., Канель А.Я. Гармония правильных многогранников. Математические этюды, 2002-2019. http://www.etudes.ru/ru/etudes/platonic-solids-harmony/
Бездетко П.В. и др. Пространственное моделирование твердотельных правильных многогранников (тел Платона) в системе AutoCAD // Наука и прогресс транспорта. Вестник Днепропетровского национального университета железнодорожного транспорта, – 2009, –№ 27, - С. 167-170. https://cyberleninka.ru/article/n/prostranstvennoe-modelirovanie-tverdotelnyh-pravilnyh-mnogogrannikov-tel-platona-v-sisteme-autocad
Альсина, К. Тысяча граней геометрической красоты. Многогранники – М.: Де Агостини, 2014. – 144 с.

Рисунки к докладу

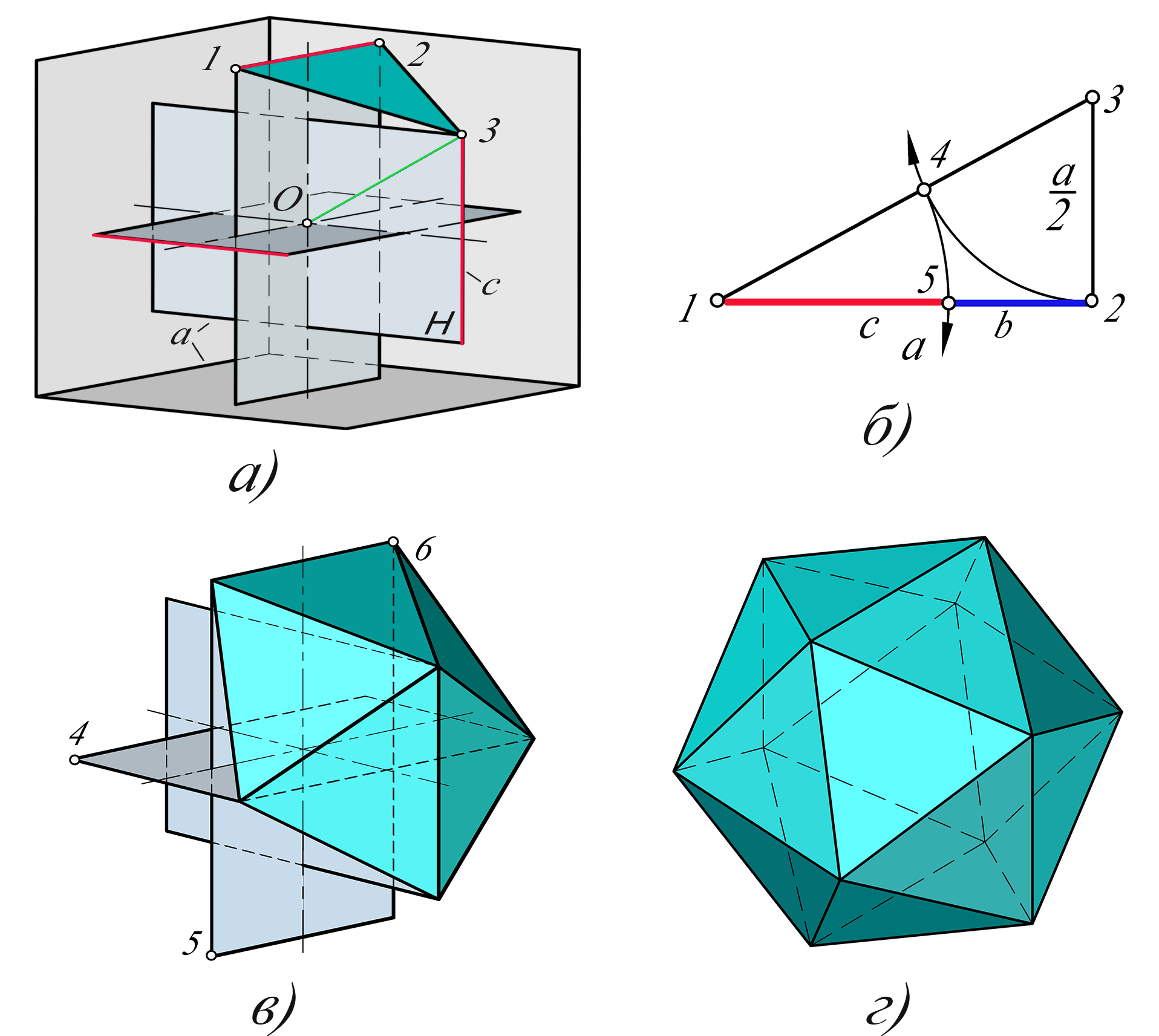
Рис. 1 Построение икосаэдра на основе золотых прямоугольников: а - модель ЗП и построение одной грани икосаэдра; б - деление отрезка в пропорции ЗС; в - построение пяти граней при одной вершине; г - модель икосаэдра

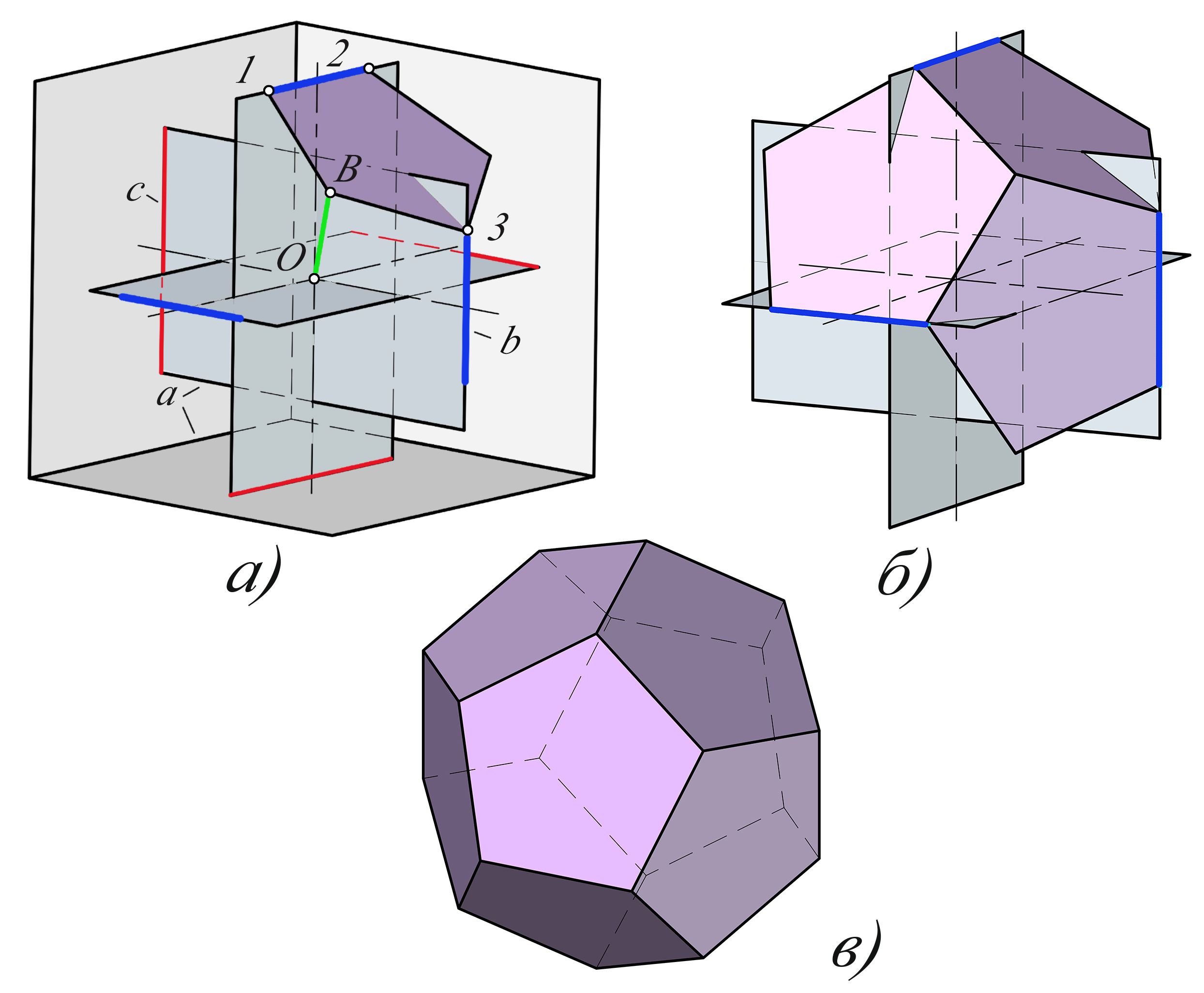
Рис. 2 Построение додекаэдра на основе прямоугольников с отношением сторон пропорции ЗС: а - модель прямоугольников для додекаэдра и построение одной его грани; б - построение трех граней при одной вершине; в - модель додекаэдра

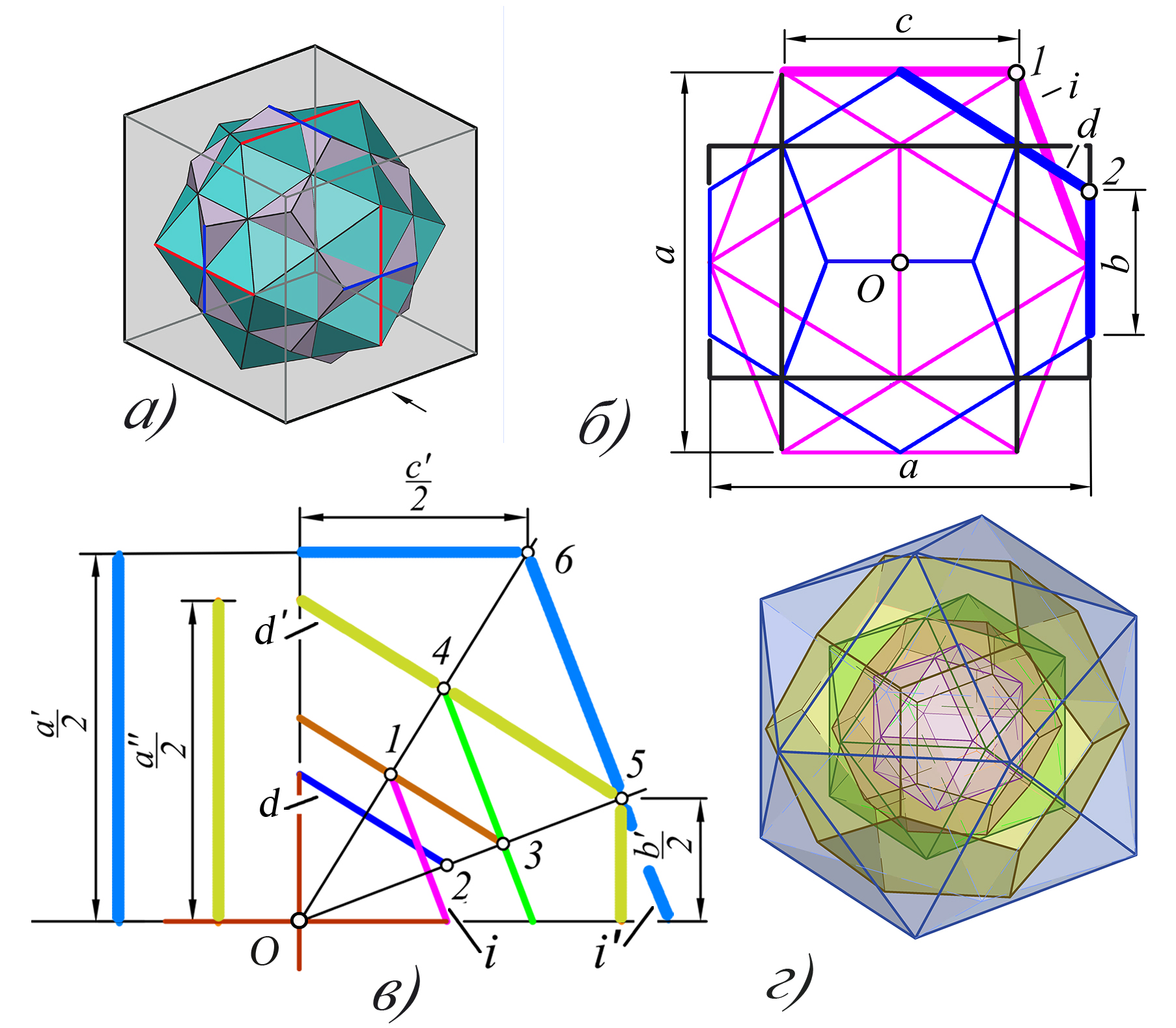
Рис. 3 Построение каскада двойственных фигур икосаэдра и додекаэдра: а - двойственное соединение дуальных многогранников; б - каркасное изображение двойственного соединения; в - схема каскада даульных фигур; г - модель каскада

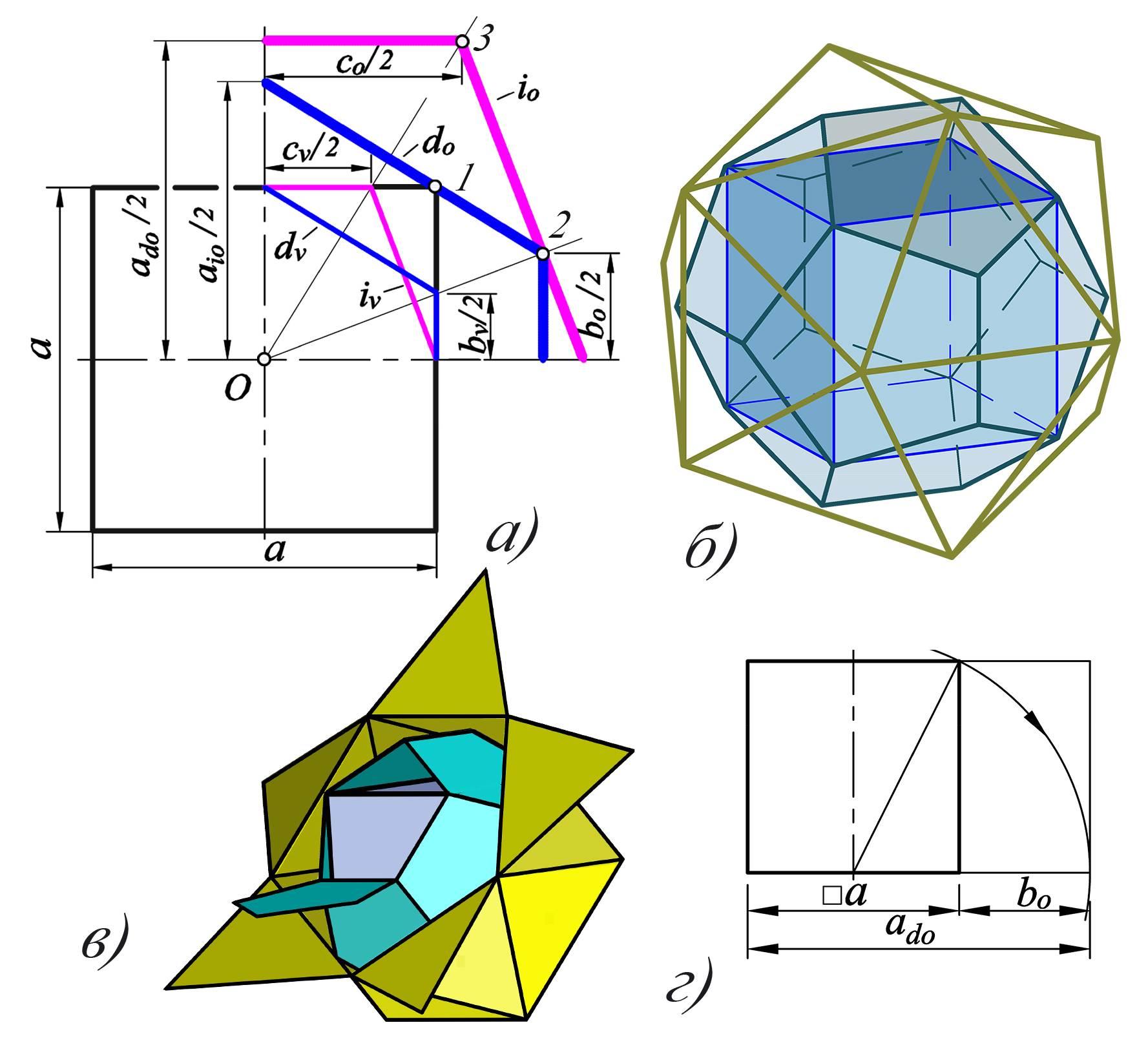
Рис. 4 Построение икосаэдра и додекаэдра, описанных около куба: а- схема для описанных фигур; б, в - модели фигур, описанных около куба; г - метод квадрата для приращения отрезка в пропорции ЗС

Вопросы и комментарии к выступлению:

Горнов Александр Олегович (11 марта 2019 г. 12:20)	Здравствуйте Вера Николаевна! Обратил внимание на Вашу работу в первую очередь потому, что её отличает четкое, ясное и аккуратное изложение как в текстовой части, так и иллюстративной. Это тот случай, когда преимущества 3D графики очевидны. Можно поздравить, что Вам удалось “закрасить” (и украсить) одно из белых пятен в области методов построения правильных многогранников данного типа. С удовольствием воспользовался рядом из большого числа интересных ссылок по теме. Спасибо. С уважением, А.
Сальков Николай Андреевич (11 марта 2019 г. 13:00)	Здравствуйте Вера Николаевна! Работа интересная, заслуживает внимания, поэтому полностью присоединяюсь к высказанным словам Александра Олеговича. В свою очередь хотелось бы сказать о том, что когда-то я говорил о работах Борисевича Игоря Александровича из Ленинграда, он, кроме всего прочего, занимался и вопросами многогранников. Посмотрите страничку https://cat.webtute.ru/author.php?id=147 В свое время пр зазговоре со мной он заявил, что разработал формулу, которая описывает все многогранники. Работу эту я не видел, а вскоре Игорь Александрович нас покинул. Мне все понравилось. А Вы не слышали о так называемом серебряном сечении? С уважением, Н. Сальков
Васильева Вера Николаевна (11 марта 2019 г. 13:16)	Добрый день, Александр Олегович! Очень приятно получить такую оценку моей работы от Вас. Хочется привести слова лауреата Нобелевской премии по физике Ф. Вельчик: «Тела Платона поддерживают вокруг себя какую-то магию. Они всегда были и остаются теми объектами, с которыми можно творить волшебство. Они уходят корнями глубоко в доисторическую пору человечества и живут сейчас…». Красота и совершенство правильных многогранников никого не оставляют равнодушным. С уважением, Вера Николаевна
Васильева Вера Николаевна (11 марта 2019 г. 13:43)	Добрый день, Николай Андреевич! Большое спасибо за внимание к моей статье. Да, о серебряном сечения я знаю, но подробно с ним не знакома. Благодарю за открытие для меня нового имени в этой теме – Борисевича Игоря Александровича. Обязательно ознакомлюсь с его трудами. С уважением, В.Н. Васильева
Селиверстов Александр Владиславович (12 марта 2019 г. 2:15)	Здравствуйте, Вера Николаевна. Благодарю за интересный и красивый доклад. Приятно отметить большое число ссылок по истории геометрии. Увы, здесь разные авторы приводят разные сведения. Обычно считается, что Теэтет Афинский первым описал икосаэдр, а додекаэдр был ещё раньше известен пифагорейцам и опубликован Гиппасом из Метапонта. Новая философская энциклопедия сообщает: "В стереометрии ему [Гиппасу] принадлежит построение додекаэдра." https://iphlib.ru/greenstone3/library/collection/newphilenc/document/HASH21249142aec8cab5b76221 Но все согласны, что именно Теэтет первым доказал, что других правильных многогранников кроме пяти известных не существует. С искренним уважением, А.В. Селиверстов
Васильева Вера Николаевна (12 марта 2019 г. 19:50)	Добрый день, Александр Владиславович! Очень признательна за внимание к статье. Отдельное спасибо за замечание и за ссылку. С уважением, В.Н. Васильева
Чередниченко Ольга Павловна (13 марта 2019 г. 16:04)	Поставила пятерку)
Селиверстов Александр Владиславович (13 марта 2019 г. 22:16)	Здравствуйте, Вера Николаевна! Нельзя ли расширить Ваш метод, чтобы построить архимедовы тела (Archimedean solids)? Например, усечённый додекаэдр (truncated dodecahedron) получается как пересечение имеющих общий центр додекаэдра и икосаэдра. Вероятно, здесь можно использовать существующий уже алгоритм построения додекаэдра и икосаэдра? То же для икосододекаэдра (icosidodecahedron) и других? С неизменным уважением, А.В. Селиверстов
Васильева Вера Николаевна (13 марта 2019 г. 23:43)	Добрый вечер, Александр Владиславович! Попробовала для икосододекаэдра, получилось. Но он, мне кажется, самый простой. Только с 3D зеркалом «крыша чуть не съехала»… Надо и остальные попробовать. Спасибо за идею. Высылаю картинку икосододекаэдра в этом окне, если дойдет. С уважением, Вера Николаевна
Селиверстов Александр Владиславович (14 марта 2019 г. 12:50)	Здравствуйте, Вера Николаевна! Очень красивый икосододекаэдр! А скорость, с которой Вы его построили, одновременно говорит о Вашем мастерстве и возможностях метода. С неизменным уважением, А.В. Селиверстов
Васильева Вера Николаевна (14 марта 2019 г. 22:21)	Добрый вечер, Александр Владиславович! Усечённые икосаэдр и додекаэдр тоже получились без проблем. Синии контуры исходных граней оставила, чтобы было понятно построение. А над ромбоикосододекаэдром, плосконосым икосододекаэдром и ромбоусеченным икосододекаэдром надо подумать. «С ходу» не знаю, как построить, опираясь на прямоугольники. С уважением, Вера Николаевна
Васильева Вера Николаевна (15 марта 2019 г. 22:07)	Добрый вечер, Александр Владиславович! Еще одно «тело» Архимеда – ромбоикосододекаэдр (РИД) готово. Построения вела на основе додекаэдра, вписанного в куб (у него взяла грани). Вот и пригодился додекаэдр, описанный около куба (у него взяла прямоугольники). Грани додекаэдра вставила на расстоянии с, равном стороне грани (красные отрезки на рис. 1), чтобы получился квадрат. Остальное, надеюсь, понятно по картинкам. Плоскости прямоугольников не стала удалять из модели (это их уголки выглядывают из РИД). С уважением, Вера Николаевна.
Селиверстов Александр Владиславович (16 марта 2019 г. 1:32)	Здравствуйте, Вера Николаевна. Надеюсь, Ваши многогранники с уголками золотых прямоугольников нравятся всем участникам. Удивительно, что в классической области, изученной в Древней Греции, можно сказать новое слово. Но Вам стоило бы собрать эти результаты, продолжая предыдущий доклад, чтобы они не остались в комментариях. Предполагается ли публикация в журнале? Кстати, цветные рисунки хорошие, но во многих журналах принимаются только рисунки в градациях серого. С неизменным уважением, А.В. Селиверстов
Васильева Вера Николаевна (16 марта 2019 г. 13:46)	Добрый день, уважаемый Александр Владиславович! Материал, с которым я ознакомила участников конференции, надеюсь опубликовать в журнале. Большое Вам спасибо за активное участие в моей работе, за замечания, подсказки и поддержку. Без Вашей идеи тела Архимеда «не нашли бы своей опоры» на прямоугольники (не пишу «золотые», т.к. у ромбоусеченного икосододекаэдра (РУИД) стороны прямоугольника не в пропорции золотого сечения, в процессе усечения вершин это свойство утратилось). РУИД строила на основе предыдущего РИД. Надо еще придумать, как построить плосконосый додекаэдр и, по-моему, больше ни одно тело Архимеда на может «опереться» на прямоугольники. Работа выполнялась под идейным руководством моего коллеги и учителя Александра Львовича Хейфеца. С искренним уважением, Вера Николаевна
Головнин Алексей Алексеевич (16 марта 2019 г. 21:16)	Здравствуйте Вера Николаевна! Не пропускаю и жду каждую конференцию КГП как возможность повысить свою квалификацию, в том числе в геометрии. На этой конференции такая работа – именно Ваша. Ваша работа показывает, как компьютер в правильных руках, уж во всяком случае, не отупляет, а полезный и умный инструмент. Ваша работа также помогает еще раз оценить гений геометров из Древней Греции, у которых не было таких геометрических инструментов, как компьютер, но они умели проводить такие глубокие исследования. Кроме того можно ведь без преувеличения отнести Вас к их соавторам? По крайней мере, в части визуализации, сделавшей их открытия доступными всем, кто этого захочет. Особо хочется поблагодарить за участие в конференции Александра Владиславовича, чьи комментарии, всегда вне сомнений квалифицированные, помогают интересующимся, но не имеющим достаточного математического образования технарям вроде меня, постигать недоступные иначе красоты геометрии. Насколько я понимаю, Вы прямо на конференции пришли к новым научным результатам. Приятно быть очевидцем такого процесса. Приятно также, что рядом с Вами есть такой единомышленник как Александр Львич, Ваш коллега. С уважением Головнин А.А.
Носов Константин Григорьевич (16 марта 2019 г. 23:47)	Добрый день, Вера Николаевна! В свое время пришлось "столкнуться" с практическим решением задачи на многогранники. Имелись фотографии изделий и их габаритные размеры, а необходимо было выдать точные чертежи граней - для нарезки их из стекла заданной толщины. Т.е. задача реверс-инжиниринга при наличии одной фотографии изделия... Задача осложнялась лишь тем, что многогранники были несимметричной формы, что-то типа искаженной формы природных кристаллов... Возможно ли, на ваш взгляд, решить подобную задачу "чисто на компьютере" без глубоких познаний в НГ? Про ручной расчет я не говорю, так как требовалась большая точность. Да и быстрее это получается, что ни говори... Пример одной из работ: (На ПК, на моделирование первой ушло минут 40 (с учетом изучения информации о многогранниках вообще), последующие, т.к. алгоритм был отработан, решались за 20-25 минут).
Васильева Вера Николаевна (17 марта 2019 г. 20:46)	Добрый вечер, Алексей Алексеевич! Большое спасибо за внимание к моей работе. Да, действительно, компьютерное 3-D моделирование и умный, и полезный инструмент для тех, кто хочет учиться, развиваться, одним словом трудиться. Прежде, чем что-либо построить на компьютере, надо хорошо подумать головой. И связь здесь взаимная, объемные построения помогают увидеть то, что трудно представить, вообразить, и нередко приводят к неожиданным подсказкам. Что было не раз и в моей работе, «провернуть в голове» все симметрии тел Платона и Архимеда, наверное, было не легко и древним грекам. Я считаю, что нам повезло: мы живем в такое время, когда есть помощник-компьютер с его трехмерной графикой. С уважением, Вера Николаевна
Васильева Вера Николаевна (17 марта 2019 г. 21:02)	Добрый вечер, Константин Григорьевич! Я думаю, у меня получилось решить эту задачу «чисто на компьютере» по одной фотографии (той, что прислали Вы, на ней в вершине кристалла две грани почему-то не состыкованы). В основании кристалла лежит правильный шестиугольник, а кристалл оказался осколком правильной шестигранной пирамиды. Поэтому высоту пирамиды взяла с подложки фотографии (строила в AutoCAD), а основание из пропорции – габариты Вы мне не сообщили. Т. к. при параллельном проецировании отношение отрезков (длины ребер пирамиды и того, что от них осталось у кристалла) не меняется, то можно у модели кристалла оставить нужную величину ребер. Дальше пирамиду рассекаем плоскостями, проходящими через ребра кристалла. На основании этих сечений строим поверхности верхних граней кристалла. Одна заминка, т.к. у меня не было высоты кристалла, пришлось его вершину взять на пересечении 2 граней приблизительно, иначе пересечение 3 поверхностей указали бы вершину. Разложив грани модели кристалла в плоскости, получим его выкройку. Интересно, по какому алгоритму строили Вы так быстро! С уважением, Вера Николаевна
Носов Константин Григорьевич (18 марта 2019 г. 10:38)	Добрый день, Вера Николаевна! Ваше решение мне понравилось, взять правильную пирамиду и отсечь... А если бы это был произвольный кристалл - угла наклона граней разные? Я решал эту задачу в SolidWorks с помощью трехмерного параметрического эскиза. А когда один каркас готов, то генерация решения с заданными размерами занимает несколько секунд. А размеры брал так-же, как и Вы - по фото, с помощью пропорций... В своем решении Вы как раз и ответили на мой вопрос - без базовых знаний НГ подобную задачу на ПК решить очень сложно. P.S. Нестыковок в моей модели нет - это просто добавлена толщина стекла, т.е. картинка уже готового изделия без оловянного каркаса.
Хейфец Александр Львович (18 марта 2019 г. 11:35)	Константин Григорьевич, Вера Николаевна несколько оробела от Вашего замечания и попросила меня, как соавтора, ответить на Ваше замечание. В SW она не работает, в AutoCAD'е, где она выполнила эту работу, трехмероной параметризации нет. Поэтому решение получено в более сложном варианте. Трехмерной параметризацией мы пользуемся, но эту работу выполнила она без нее. Но основной наш к Вам вопрос - где Вы увидели здесь НГ? Нет ее здесь, не понадобилась. Может, Вы имеете ввиду пропорциональное деление отрезков на основе фотографии, так это ГЕОМЕТРИЯ. Итак, где Вы увидели НГ в данной работе? С уважением. Вера Николаевна, Александр Львович.
Носов Константин Григорьевич (18 марта 2019 г. 19:41)	Александр Львович! Не буду с Вами "спорить", не хочу отнимать эту "радость" у Николая Андреевича :-) Хотя я придерживаюсь некой середины между вашими мнениями, но оказаться между двумя мэтрами НГ и КГ мне не улыбается. Я практик и к каждой задаче подхожу с практической точки зрения, в том числе с позиции рациональности и целесообразности. Если мне быстрее решить на компьютере и он под рукой, то я решу на нем, а если не дай Бог я окажусь на необитаемом острове, то я бы хотел быть "вооруженным" знаниями как герой книги Жуль Верна "Таинственный остров". Никаких замечаний, Вере Николаевне, я не делал... Наоборот - впечатлен... По сути, применительно к моему "мыслительному аппарату": Есть фото изделия, необходимо получить чертежи составных частей. Смотрю на фото и понимаю, что это аксонометрия (перспективой пренебрегаем, ввиду незначительности погрешности) - векторизирую (можно ручками, в CAD проложить линии по ребрам кристалла, а можно в CorelDraw, автоматически получить векторный рисунок). По заданным габаритам определяю положение осей и коэффициенты, а по ним и размеры всех ребер. Далее..., я уже писал. Так вот, весь произошедший процесс был выполнен на основе знания закономерностей аксонометрического чертежа. Один из главных принципов НГ - обратимость чертежа выполнен на практической задаче. Если это можно сделать как-то по другому, то это прекрасно, но я по-другому не смог.
Соколова Людмила Сергеевна (21 марта 2019 г. 16:22)	Еще одна пятерка в Ваш золотой результат, уважаемая Вера Николаевна! Понимаю гордость Александра Львовича за Ваши достижения. Новых успехов в вашем содружестве! Л.С.Соколова
Соколова Людмила Сергеевна (22 марта 2019 г. 15:49)	Здравствуйте, уважаемая Вера Николаевна! Наконец отыскала нужную статью ( пополнит Вашу коллекцию литературы): Д.И.Перепелкин "Об одном построении правильного икосаэдра и правильного додекаэдра". Математическое просвещение, 1937г., №12, с.10-15 Некоторое время назад мы построили эти фигуры в соответствии с рекомендациями статьи на компьютере с использованием Компаса и Inventora. Оба студента сказали: " Фи! Нет объема, изображение плоское" и прекратили дальнейшую работу. Интересно, известен ли Вам этот способ? Автор писал,что "...построение, о котором идет речь, позволяет сравнительно просто вывести основные метрические соотношения в правильных икосаэдре и додекаэдре, вовсе не прибегая к тригонометрии и основываясь исключительно на делении отрезка в среднем и крайнем отношении" ( прямо под компьютер). Очень интересно Ваше мнение о полученном нами результате. Спасибо.Л.С.Соколова.
Васильева Вера Николаевна (23 марта 2019 г. 0:17)	Добрый вечер, Людмила Сергеевна!!! Три восклицательных знака, т.к. именно «ЭТО» я искала. Спасибо большое за Д.И. Перепелкина "Об одном построении правильного икосаэдра и правильного додекаэдра". Математическое просвещение, 1937г., №12. Книга Д.И. Перепелкина «Курс элементарной геометрии», часть 2, Геометрия в пространстве, М.-Л., 1949, С. 345. у меня есть в формате «DJVU», но почему-то я ее обошла вниманием. Впрочем, там не оказалось нужного способа построения додекаэдра. Построение икосаэдра описывается Перепелкиным классически, по сути, на основании золотых прямоугольников-ЗП, хотя он их так не называет и не изображает. В подсказанной Вами работе 1937 г. начало построения додекаэдра ведется на основе отрезков пропорции золотого сечения, а в конце сведено к вписыванию куба и, по-моему, к методу «крыш» – они видны. Понятно, что без компьютерных технологий в то время иначе было нельзя. Да, такой способ для икосаэдра мне был известен (о чем я пишу в статье), а способ для додекаэдра я дополнила сама. Радует, что вначале мы с Д.И. Перепелкиным мыслили одинаково, но благодаря 3D моделированию, я завершила построение более коротким путем. Не понятно, почему Ваши студенты не увидели в этом способе объема? Разве они строили не объемные модели, или не могли преобразовать поверхности в 3D тела? Способ, действительно, под компьютер. Эти работы проводились вне занятий? Полученной результат лишний раз подтверждает «ясность рассуждений» и наглядность объемных построений икосаэдра и додекаэдра на основе прямоугольников пропорций золотого сечения. С уважением и благодарностью, Вера Николаевна

Назад Go Back