ВИЗУАЛИЗАЦИЯ ГЕОМЕТРИЧЕСКИХ ФИГУР И ОТНОШЕНИЙ КОМПЛЕКСНОЙ ПЛОСКОСТИ СРЕДСТВАМИ КОМПЬЮТЕРНОЙ ГРАФИКИ

В статье рассматриваются вопросы наглядного представления геометрических фигур и отношений комплексной плоскости на трехмерном гиперэпюре, для построения которого используются возможности компьютерной графики.

Введение

Необходимость иметь дело при решении геометрических задач не только с действительными, но и с мнимыми фигурами (точками, линиями) связана с тем, что евклидова геометрия не замкнута и ее дополняет псевдоеклидова геометрия мнимых фигур [1]. Наглядным примером этого может служить тот факт, что всякое квадратное уравнение (к такому уравнению сводится, например, нахождение точек пересечения прямой и окружности) имеет два решения – действительных различных, действительных совпавших или мнимых. В первом случае прямая и окружность имеют две точки пересечения, во втором – касаются (точки пересечения совпадают), а в третьем – точки пересечения оказываются мнимыми, то есть перестают быть элементами евклидовой геометрии. Мнимые фигуры (точки и линии) комплексной плоскости часто возникают при решении научных и прикладных задач [1-8], в частности на настоящей конференции мнимым фигурам в геометрических задачах посвящены доклады [9-11]. В последнее время интерес к ним возрос, благодаря возможностям современных систем конструктивного геометрического моделирования [3, 5, 12, 13]. Тем не менее, использование их на практике существенно осложняется тем, что сами эти фигуры и их свойства не могут быть продемонстрированы непосредственно (наглядно). В перечисленных выше работах при решении задач с фигурами комплексной плоскости применяются те или иные способы их задания и представления, однако для отображения используется плоскость, при этом сами фигуры, их мнимые продолжения показываются скорее условно (обозначения типа векторов, маркеров, марок, пунктирных линий и др.), чем наглядно, и в качестве фигур выступают преимущественно их реперы. Таким образом разработка способов наглядного представления мнимых фигур комплексной плоскости и их свойств является актуальной проблемой.

Отметим, что большинство прежних работ, посвященных вопросам использования и представления мнимых фигур комплексной плоскости, были ограничены необходимостью минимизировать и упрощать построения. Возможности современных компьютерных систем в области точности геометрических построений, их автоматизации и простоты применения трехмерной графики, в значительной мере снимают это ограничение.

В настоящей работе предлагается отображать геометрические фигуры и отношения комплексной плоскости, главным образом, при помощи трехмерного гиперэпюра (типа гиперэпюра Наумович), получаемого по методу Монжа ортогональным проецированием четырехмерного пространства с системой координатных осей (x, x_i, y, y_i), являющегося моделью комплексной плоскости, в картинное трехмерное пространство. Для создания таких проекций разработано специальное программное обеспечение, а также используется способ передачи трехмерных проекций в виде точечных каркасов поверхностей в САПР типа «Компас-3D», где могут выполняться пространственные геометрические построения. Далее эти вопросы будут рассмотрены более подробно.

1. Формирование моделей фигур комплексной плоскости

Комплексная плоскость – это множество точек A(ẋ, ẏ), где ẋ и ẏ – комплексные числа вида a+ia_i (a и a_i – действительные числа), таким образом всякая точка A комплексной плоскости задается четверкой независимых чисел (x^A, x_i^A, y^A, y_i^A) и может быть однозначно представлена точкой четырехмерного евклидова пространства или парой независимых (в отличие от связанных тем или иным условием проекций точки трехмерного пространства) точек евклидовой плоскости. Далее мы будем рассматривать только огранченный отсек собственных точек комплексной плоскости. Отметим, что при графическом моделировании так обычно и делается, поскольку любой чертеж ограничен некоторым участком плоскости.

Также мы будем рассматривать множества точек, координаты которых удовлетворяют уравнениям вида F (ẋ, ẏ) = 0. На евклидовой плоскости эти множества точек представляют собой линии (прямые, окружности и т.д.). Поскольку после отделения частей с i такие уравнения приводятся к системам уравнений вида:

– в нашей модели комплексной плоскости таким системам уравнений соответствуют множества точек размерности ∞², то есть поверхности (2-поверхности), которые в общем случае могут быть искривлены в четырехмерном пространстве и не принадлежать никакому трехмерному подпространству, то есть не иметь трехмерной натуральной величины. Наглядное их представление на плоскости, в общем случае, затруднительно [14]: каждая точка картинной плоскости соответствует некоторой плоскости четырехмерного пространства, в результате чего не только проекция самой поверхности, как правило, совпадает с картинной плоскостью, но и линии уровня могут вырождаться в точки, а сетки различных линий уровня совпадать или перекрывать друг друга. Поэтому основным способом для представления таких фигур мы будем считать построение их различных пар трехмерных проекций (см. подробее в [15]). В частности, введем четыре системы таких пар проекций (комплексные двухкартинные модели – гиперэпюры) – x_i-xOy-y_i, y-xOx_i-y_i, x-yOy_i-x_i, x-x_iOy_i-y (в обозначении указаны: вертикальная ось верхней проекции – базовая плоскость – вертикальная ось нижней проекции). Первые три модели содержат плоскость xOy и действительные образы исследуемых фигур без искажения, причем в модели x_i-xOy-y_i мнимые продолжения естественным образом «дополняют» действительный образ. Проекциями 2-поверхностей четырехмерного пространства, в общем случае, будут некоторые поверхности трехмерного пространства. В частном случае проекцией 2-поверхности может быть некоторая линия.

Рассмотрим моделирование некоторых фигур комплексной плоскости на плоскости и при помощи трехмерных проекций.

Модель точки комплексной плоскости

Одно из первых изображений мнимых фигур на чертеже дано Понселе в «Трактате о проективных свойствах фигур» (1822) (цитируется по [16]), и представляет собой известное построение мнимых точек пересечения коники и прямой. Этот способ и в настоящее время широко применяется, например, в [6]. Вообще, комплексно сопряженные точки играют важную роль, поскольку при решении задач с действительными фигурами (например, при пересечении действительной прямой и действительной коники) всегда появляются парами (точки N' и M' на рис. 1). Через пару таких точек всегда можно провести действительную прямую, на которой они задают эллиптическую инволюцию [1].

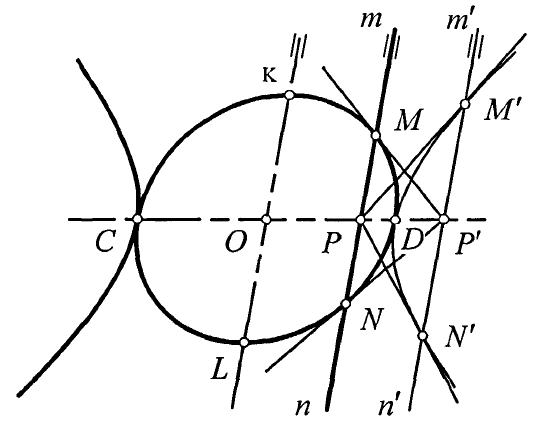
Рис. 1. Воспроизведение чертежа из работы Ж.-В. Понселе о построении «реальных и идеальных» хорд конического сечения

Историческую справку о различных способах представления мнимых точек на чертеже можно найти в [1, 16, 7]. Мы отметим следующие способы изображения на чертеже мнимых точек:

• «маркер» x(O, L) [1, 5], который содержит прямолинейный ряд x и точку Лаггера L (рис. 2, а) – такое задание позволяет легко выполнять построения точек, соответственных в эллиптической инволюции, которая инициируется на прямой x парой комплексно сопряженных точек (сами точки не показываются);
• векторная аксонометрия П.В. Филиппова [7] – здесь три координатные оси четырехмерного пространства отображаются, как на обычном аксонометрическом чертеже, а оставшаяся четвертая координата – дополнительно изображается вектором заданного направления (рис. 2, б)
• пара независимых проекций точки на плоскостях проекций xOy и x_iOy_i, как это делается, к примеру, в системе «Симплекс» [3, 12, 13] (рис. 2, в);
• векторное представление, в котором начало вектора помещается в точку с действительными координатами (x^A, y^A), а конец – в точку с координатами (x^A+x_i^A, y^A+y_i^A) (рис. 2, г).

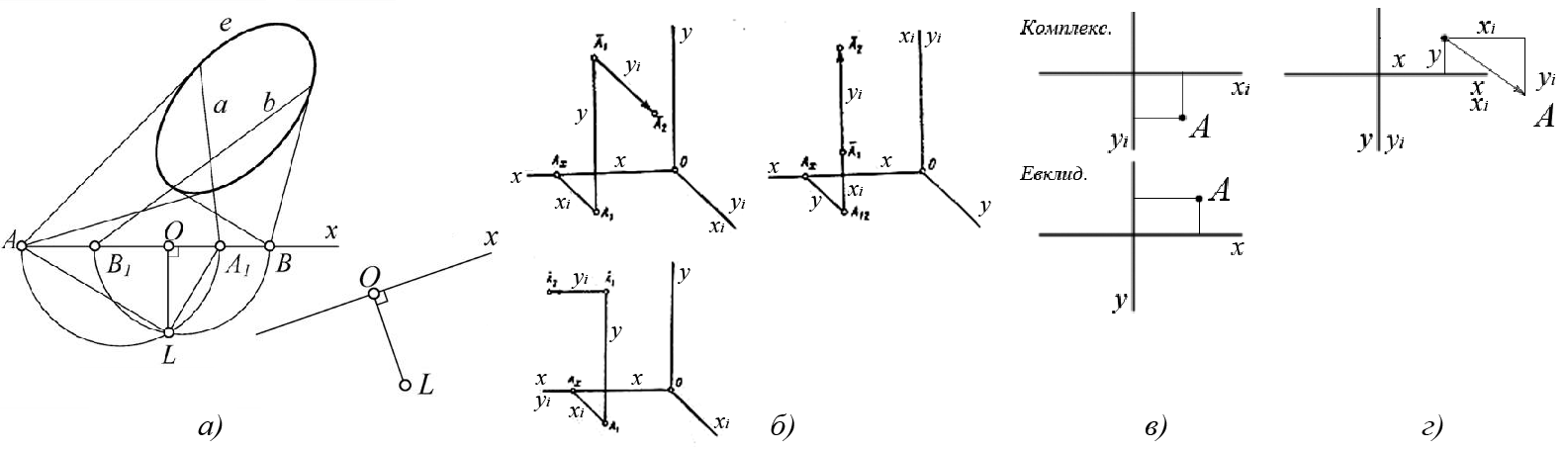
Рис. 2. Различные способы отображения мнимых точек на плоскости

Основанные на инволюционных свойствах мнимых точек способы их отображения (в частности, «маркеры») имеют дело с парами комплексно сопряженных точек, в то время как последние три способа – координатные – позволяют изобразить каждую мнимую точку в отдельности.

Укажем на связь векторного способа представления мнимой точки с использованием «маркеров». Пара комплексно сопряженных мнимых точек (M₁ и M₂) при векторном способе изображается двумя равными по длине противоположно направленными векторами с общим началом O, концы этих векторов и точка Лаггера L лежат на общей окружности с центром в точке O и задают действительную прямую x – носитель эллиптической инволюции [1]. Это позволяет довольно легко переходить от векторов к «маркерам» и наоборот (рис. 3, а), а от векторного представления – к другим координатным. Поскольку большинство современных языков программирования содержат встроенные средства для вычислений с комплексными числами, то подпрограммы, выполняющие расчет координат точек пересечения линий по общим формулам, формируют комплексные координаты автоматически и не требуют реализации дополнительных построений. Изображение, показанное на рис. 3, б, получено автоматически как результат пересечения окружностей с прямыми пучка с собственным центром Q и пучка с несобственным центром в интерпретаторе языка геометрических построений [17]. На рис. 3, в показаны чисто мнимые проекции тех же точек (чисто действительные присутствуют на рис. 3, б как точки в началах векторов), комплексно сопряженные пары соединены отрезками. На рис. 3, г показана одна из проекций П.В. Филиппова тех же точек.

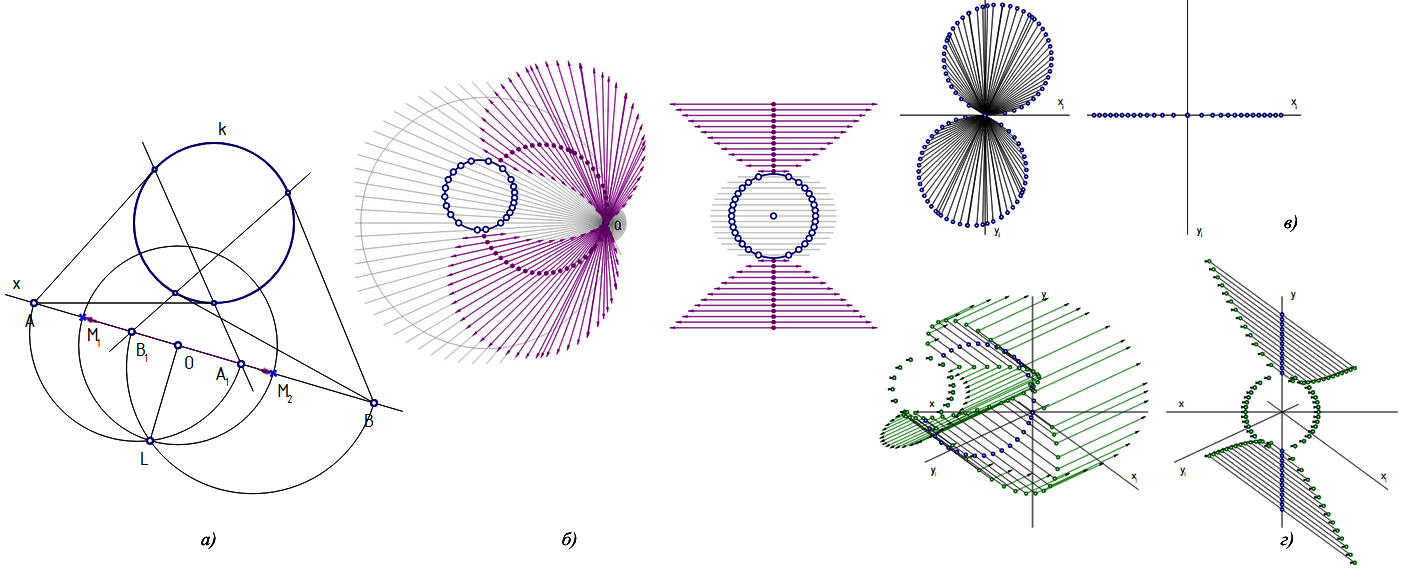
Рис. 3. Связь векторной формы и «маркера», использование различных способов отображения мнимых точек

Как видно из примеров, для обратимого и наглядного моделирования точек вполне достаточного плоского чертежа. Векторное представление оказывается в этом случае наиболее естественным: изображение строится на одной картинной плоскости и все координаты откладываются без искажения.

Модель линии комплексной плоскости

Выше отмечалось, что линии комплексной плоскости представляют собой точечные многообразия размерности ∞², то есть поверхности. Рассмотрим некоторые ранее встречавшиеся способы их представления.

В [18] рассматриваются модели функций комплексного переменного, которые представлены поверхностями трехмерного пространства, так называемыми модулярными – в качестве аппликаты точки поверхности используется модуль функции для данного комплексного значения аргумента, но такие модели не содержат достоверной информации обо всех компонентах координат точки и не позволяют решать обратную задачу.

В [7] для наглядного моделирования функций комплексного переменного используются векторные аксонометрии, но, в действительности, такие изображения трудночитаемы, особенно в случае многозначных функций. Например, на рис. 4, а показана модель прямой u+i∙v=a∙x+b+i∙a∙y.

В [19] строятся мнимые продолжения коник в виде трехмерных поверхностей для наглядного отображения свойств инцидентности мнимых точек коникам и пересекающимся с ними прямым. Полученная в результате поверхность («полная коника») отражает только мнимые продолжения, соответствующие заданному направлению пересекающих конику прямых (рис. 4, б).

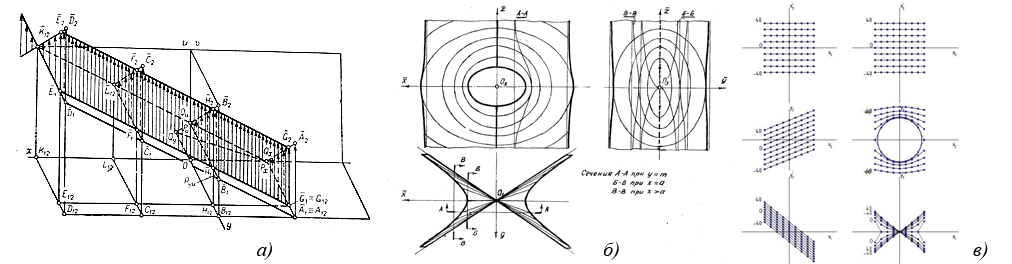
Рис. 4. Моделирование линий комплексной плоскости

Моделирование такой поверхности на комплексном чертеже при помощи каркаса линий (способ топографической поверхности) также оказывается не очень наглядным. На рис. 4, в показаны проекции каркаса линий мнимой прямой (слева) и действительной окружности (справа). Построенные линии лежат в пространствах x_i=const. Если чертеж мнимой прямой достаточно понятен, поскольку линейная функция однозначна, то чертеж окружности состоит из перекрывающих друг друга линий на пересекающихся листах поверхности, так что прочитать такой чертеж и показать на нем, к примеру, пересечение прямой с окружностью или двух окружностей проблематично.

Поэтому для отображения поверхностей, являющихся линиями комплексной плоскости, будем строить линейный или точечный каркас такой поверхности и получать две его ортогональные трехмерные проекции (см. подробнее [15]). Проекции отдельных точек поверхности можно при необходимости соединить линиями связи, которые будут перпендикулярны общей плоскости двух трехмерных проекций. Для полученной модели пространства справедливы общие свойства проецирования: проекциями точек являются точки, линий – в общем случае линии, порядок алгебраических кривых сохраняется для проекций, сохраняются принадлежность точек, касание, параллельность и др.

Формирование точечного каркаса модели линии и передача его в САПР «Компас-3D»

Для создания изображений, не требующих выполнять геометрические построения, будем использовать специальный редактор, созданный на основе технических возможностей библиотек трехмерной графики (OpenGL/WebGL) и встроенных в язык программирования вычислительных подпрограмм для работы с комплексными числами. Формирование точечного каркаса для линии, которая определяется уравнением вида F(ẋ, ẏ)=0, выглядит следующим образом:

• Считая ẋ константой, необходимо привести уравнение к виду f(ẏ)=0.
• Составить алгоритм нахождения решений уравнения f(ẏ)=0, получить выражения для вычисления ẏ=ẏ(ẋ).
• Изменяя ẋ на некотором прямоугольнике значений (a≤x≤b, a'≤x_i≤b'), получить соответствующие недостающие координаты ẏ точек поверхности. Варьируя шаг изменения x и x_i, можно добиться приемлемой плотности каркаса. В результате будет сформирован двумерный массив двоек (ẋ, ẏ) или после разделения комплексного типа данных на вещественные компоненты – массив четверок (x, x_i, y, y_i).
• Двумерный массив дает возможность формировать каркас условных образующих поверхности двумя способами: либо использовать первый индекс как индекс образующей, а второй – как индекс точки на ней, либо наоборот. Это позволяет выбирать наилучший способ обхода точек при отображении модели. Если ни один из указанных способов не подходит, уравнение F(ẋ, ẏ)=0 следует раскрыть, считая константой ẏ, и сформировать массив координат на прямоугольнике значений ẏ (c≤x≤d, c'≤x_i≤d').
• В соответствии с выбранной системой проекций выполнить отображение точек в две трехмерные проекции.

В некоторых случаях нам потребуется не только визуальное представление фигур комплексной плоскости, но и геометрические построения с ними. Для этих целей будем использовать следующий подход.

• Точечный каркас модели линии будем передавать в САПР, причем, каждую проекцию необходимо передавать отдельно.
• В САПР на основе точечного каркаса будем строить вспомогательные поверхности, каждая из которых с некоторой точностью аппроксимирует проекцию исходной модели линии комплексной плоскости.
• При помощи встроенных средств САПР будем выполнять построения – создавать вспомогательные плоскости, пересекать плоскости с поверхностями и полученные линии между собой, находить проекции линий и т.п.

Для воссоздания поверхности по каркасу в системе «Компас-3D» предназначена команда «Поверхность по сети точек». Система «Компас-3D» может импортировать точечный каркас поверхности в виде текстового файла или таблицы MS Excel. Формат текстового файла должен быть следующим:

X1.1 Y1.1 Z1.1
X1.2 Y1.2 Z1.2
...
X1.k Y1.k Z1.k
*
X2.1 Y2.1 Z2.1
X2.2 Y2.2 Z2.2
...
X2.k Y2.k Z2.k
*

...

Xm.1 Ym.1 Zm.1
Xm.2 Ym.2 Zm.2
...
Xm.k Ym.k Zm.k
*

Точечный каркас передается сериями по k-точек, координаты которых записываются в строку (в качестве десятичной запятой используется знак «.»). Серия точек определяет точечный каркас одной из линий поверхности. Конец серии обозначается знаком «*». Переданные таким образом серии точек преобразуются в сплайновые кривые, на которые далее система натягивает сплайновую поверхность. Очевидно, полученная таким образом поверхность в САПР отличается от исходной проекции линии комплексной плоскости, однако, выбирая подходящую плотность и распределние точек и линий каркаса поверхности, можно добиться приемлемой точности замены.

Другая сложность заключается в том, что, как будет показано ниже, проекции линий комплексной плоскости выше первого порядка имеют сложную топологическую структуру – самопересекающиеся листы, разрывы. При попытке построить сплайновую поверхность через такой точечный каркас возникают ошибки топологии, разрывы затягиваются поверхностью и т.п., поэтому в каждом случае экспорт в САПР сгенерированного точечного каркаса чувствителен к способу обхода точек при экспорте и может потребовать дополнительных усилий.

2. Визуальные образы прямых и кривых второго порядка

Рассмотрим полученные описанным выше способом проекции линий комплексной плоскости – прямых и кривых второго порядка, а также некоторые их свойства, проявляющиеся на трехмерных проекциях.

Прямые комплексной плоскости

Многие важные свойства комплексных прямых, в том числе моделирование их на плоскости при решении конструктивных задач рассмотрены в работах [1, 6, 20]. Рассмотрим вопросы наглядного моделирования прямых комплексной плоскости. На рис. 5 показаны векторные чертежи точечного каркаса и линейный каркас на чертеже Радищева действительной (слева) и мнимой (справа) прямых.

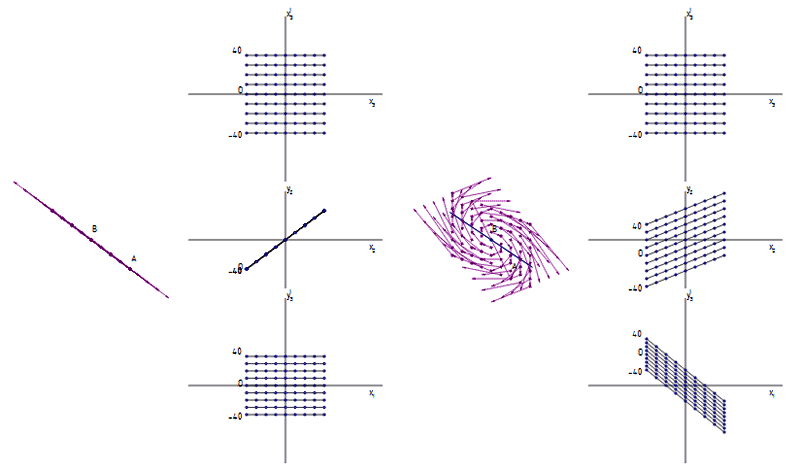
Рис. 5. Плоские модели каркасов прямых комплексной плоскости

Все векторные проекции точек действительной прямой лежат на ее следе в плоскости xOy. Векторные проекции точек мнимой прямой образуют сложную для понимания и восприятия сеть, что подтверждает высказанное выше замечание о целесообразности применять именно трехмерные проекции для моделирования линий комплексной плоскости.

Рассмотрим образование трехмерных проекций прямой. Прямая задается линейным уравнением относительно переменных ẋ и ẏ: , где ȧ, ḃ и ċ – комплексные числа, которое можно привести к системе:

                                              (1)

Каждое уравнение системы (1) задает 3-пространство общего положения, проекции которого в картинных пространствах не различимы (совпадают с ними). При помощи умножения и сложения уравнений можно избавиться от одной из четырех переменных, то есть перезадать комплексную прямую пересечением пары 3-пространств частного положения. Например, для модели x_i-xOy-y_i:

                  (2)

Прямые действительной плоскости условно можно разделить на четыре класса: горизонтальные – y=const (∞¹ прямых), вертикальные – x=const (∞¹ прямых), проходящие через начало координат – ax+by=0 (∞¹ прямых) и общего положения – ax+by+c=0 (∞² прямых). Прямые комплексной плоскости более разнообразны. Общее число таких прямых на комплексной плоскости составляет ∞⁴. Среди них можно выделить две связки (∞² элементов) прямых, имеющих вырожденные проекции (проекции в виде обыкновенных прямых) в картинных пространствах (ẋ=const и ẏ=const), связку действительных прямых (a_i=b_i=0, трехмерные проекции которых расположены перпендикулярно к плоскости xOy), связку прямых, трехмерные проекции которых расположены перпендикулярно к плоскостям x_iOy и xOy_i, и ∞⁴ комплексных прямых общего вида, имеющих проекции в виде пары плоскостей общего положения (см. в [15]). Последние наиболее интересны, поскольку пара плоскостей общего положения позволяет задать ∞³∙∞³=∞⁶ фигур, в то время как комплексных прямых всего ∞⁴. Это означает, что пары таких проекций связаны дополнительными условиями (подобно тому как на плоскости пары проекций точек трехмерного пространства связываются линиями связи). Для исследования ∞⁴ прямых общего вида достаточно исследовать связку (∞²) прямых, проходящих через начало координат O(0,0,0,0). Любая другая прямая комплексной плоскости оказывается параллельна какой-то прямой этой связки, а именно, если прямая задана парой точек A(x^A, x^A_i, y^A, y^A_i) и B(x^B, x^B_i, y^B, y^B_i), то она будет параллельна прямой, проходящей через начало координат и точку F(x^B-x^A, x^B_i-x^A_i, y^B-y^A, y^B_i-y^A_i). Последнее легко проверить, подставляя координаты точек A, B, O и F в систему (1). Уравнения линейных 3-пространств, задающих комплексную прямую, будут различаться только значениями коэффициентов c и c_i. Точке F исследуемой прямой придавались различные значения координат и были получены следующие случаи расположения трехмерных проекций:

На рис. 6, а-5, б показаны модели прямых x=0 и y=0 (тип 0), соответственно. Модели других прямых типа 0 (x=const и y=const) получаются сдвигом вырожденной проекции (проекции в виде обыкновенной проецирующей прямой) параллельно плоскости xOx_i или yOy_i, соответственно. Это позволяет получить ∞² вырожденных проекций, которые инцидентны ∞² точек плоскости xOx_i или yOy_i, соответственно, то есть задать любую прямую указанных связок.

На рис. 6, в показаны модели прямой ax+by=0 (тип 1), проекции которой перпендикулярны одновременно плоскостям xOy и x_iOy_i. Такая прямая в трехмерной модели однозначно задается следами в плоскостях xOy и x_iOy_i (причем эти следы образуют попарно одинаковые углы с осями x и x_i и y и y_i, соответственно). Модели других прямых типа 1 получаются параллельным сдвигом следов в плоскостях xOy и x_iOy_i (коэффициенты c и/или c_i в (1) отличны от 0). К этому типу относятся все действительные прямые общего вида: след действительной прямой в xOy может проходить на произвольном расстоянии от O (определяется коэффициентом уравнения c), в то время как след в плоскости x_iOy_i – всегда проходит через O (коэффициент c_i=0).

На рис. 6, г показаны модели прямой ax+iby=0 (тип 2), проекции которой перпендикулярны одновременно плоскостям xOy_i и x_iOy. Частным случаем таких прямых являются изотропные прямые.

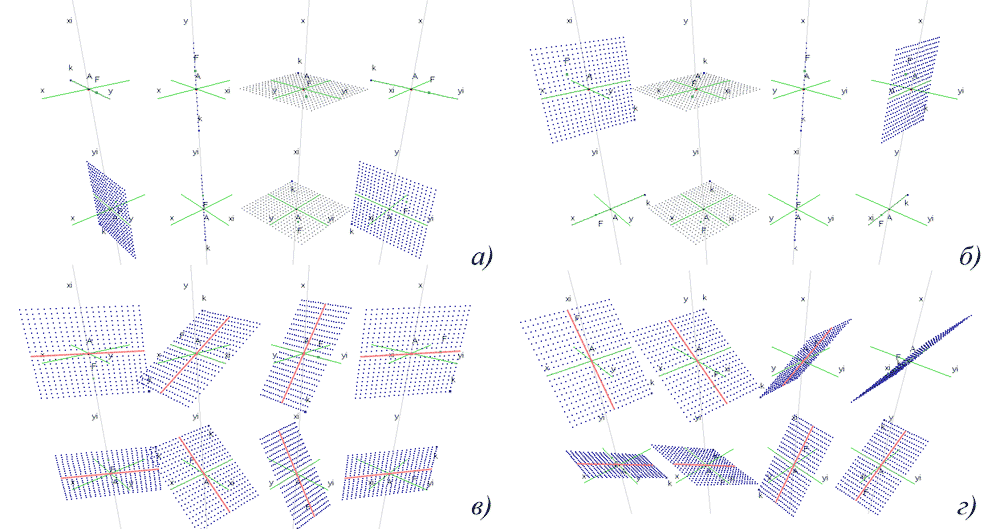
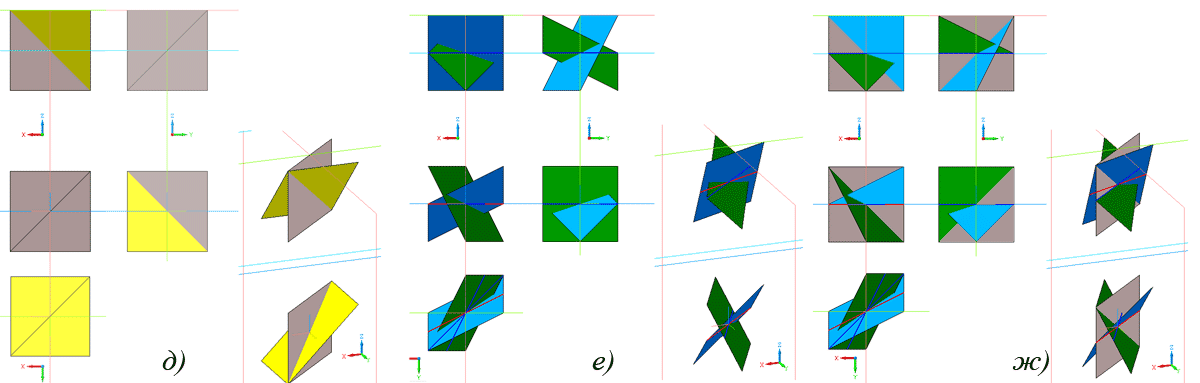Рис. 6. Моделирование прямой комплексной плоскости

На рис. 6, д-ж показаны отсеки трехмерных проекций комплексных прямых на модели x_i-xOy-y_i, переданные в систему «Компас-3D». На рис. 6, д изображены действительная прямая x–y=0 (тип 1 – сиреневый цвет) и изотропная x–iy=0 (тип 2 – желто-коричневый). На рис. 6, е показаны две прямые типа 3, полученные для разных комбинаций координат второй точки (случай 8 – зеленая и 15 – голубая), синим и красным цветом показаны следы проекций в плоскости xOy. На рис. 6, ж показаны те же прямые и для сравнения действительная прямая (розовый цвет). На рис. 7, а показана модель комплексной прямой общего вида (случай 16 – голубой цвет), для сравнения также показаны комплексная прямая типа 3 (зеленый цвет) и действительная прямая (сиреневый цвет). Проекциями комплексной прямой общего вида в большинстве случаев являются две плоскости общего положения, однако возможны случаи (например, 16а в таблице), когда вторая мнимая точка с ненулевыми значениями всех четырех координат задает действительную прямую. Вероятно, другие соотношения координат могут задавать мнимые прямые типа 2 и 3. Можно сделать вывод о необходимости дальнейшего исследования свойств комплексных прямых типа 3 и общего вида и их трехмерных проекций.

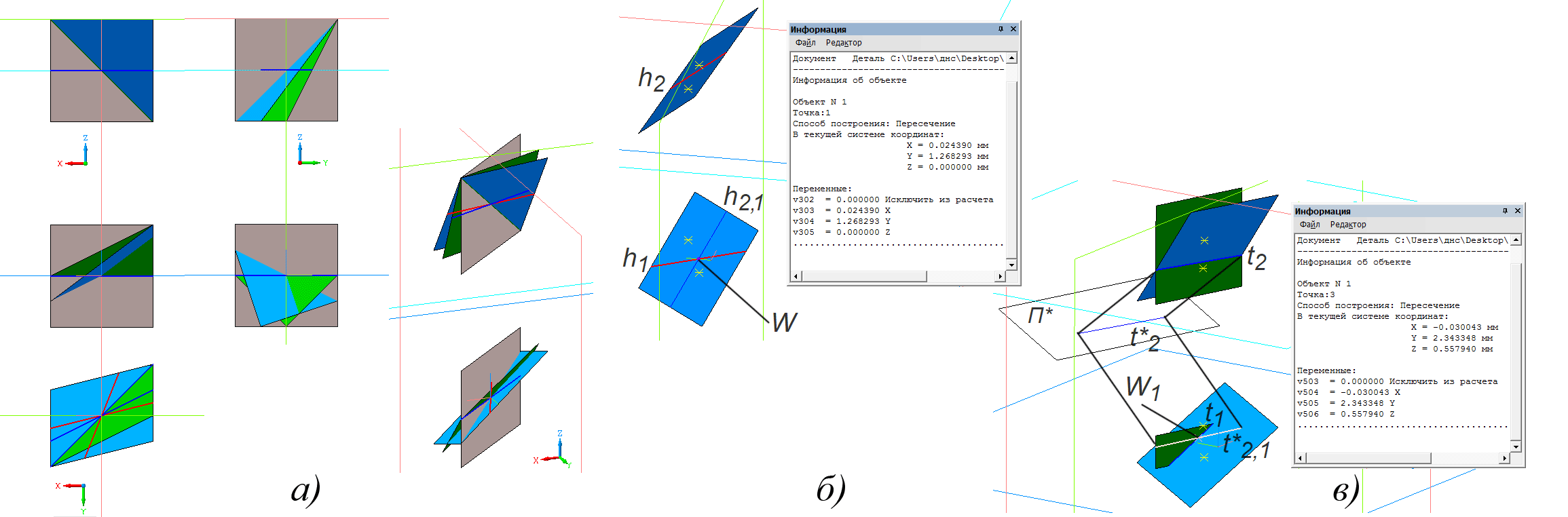Рис. 7. Модели отсеков прямых комплексной плоскости и решение задач в системе «Компас-3D»

Рассмотрим решение двух конструктивных задач, связанных с комплексными прямыми, на трехмерных моделях в системе «Компас-3D».

Задача 1. Найти действительную точку комплексной прямой типа 3 или общего вида (рис. 7, б).

Будем использовать модель x_i-xOy-y_i. Найдем следы h₁ и h₂ (показаны красной линией) нижней (П₁) и верхней (П₂) проекций прямой в плоскости xOy, спроецируем след h₂ с верхней проекции на плоскость xOy нижней проекции либо на нижнюю проекцию комплексной прямой (h_2,1 – синяя линия), где найдем точку W пересечения h₁ и h_2,1. Эта точка – искомая. Трехмерные координаты точки на проекции П₁ в системе «Компас-3D» – x, y, z, – соответствуют координатам x, y, y_i точки комплексной плоскости. На рис. 7, б показано построение действительной точки мнимой прямой, заданной парой комплексных точек с координатами (-1, 1, 1, -1) и (1, -2.5, 2.5, 1.5). С учетом округления результаты, полученные конструктивным способом в системе  «Компас-3D» и на основе вычислений с комплексными числами в программе, дали один и тот же результат.

Задача 2. Найти точку пересечения двух комплексных прямых, одна из которых мнимая (рис. 7, в).

Рассмотрим пересечение прямых, одна из которых действительная. В случае двух мнимых прямых построения будут еще проще, так как точки с верхней на нижнюю проекции прямой и наборот можно проецировать непосредственно. Найдем линии пересечения соответствующих проекций прямых t₁ и t₂ (показаны синим). Установим соответствие между проекциями действительной прямой при помощи вспомогательной плоскости П*. Спроецируем t₂ на П*, получим t*₂ и затем на нижнюю проекцию действительной прямой (t*_2,1). Найдем точку пересечения t₁ и t*_2,1 – W₁ и ее вторую проекцию (W₂). На рис. 7, в показано пересечение прямой из задачи 1 с действительной прямой, заданной точками (1, 0, 2, 0) и (-2, 0, 3, 0). Вычислительным способом были найдены следующие координаты общей точки – (-0.030042918454935622, - 1.6738197424892705, 2.3433476394849784, 0.5579399141630901). Координаты точки, найденной в системе «Компас-3D», показаны на рисунке. Сравнение полностью подтверждает правильность конструктивного решения.

Таким образом предлагаемая модель на основе трехмерных проекций позволяет достаточно просто и более наглядно, чем плоский чертеж, представлять прямые комплексной плоскости, решать задачи принадлежности точки, взаимного пересечения и др. Для прямых типа 0–2 существуют очевидные и простые конструктивные способы построения трехмерных проекций, не требующие вычислений с комплексными числами. Проекции прямых типа 3 и общего вида в рассмотренных выше примерах строились вычислительным способом. Представляет интерес дальнейшее их исследование, в частности, разработка алгоритмов конструктивного и по-возможности простого нахождения их трехмерных проекций.

Окружности комплексной плоскости

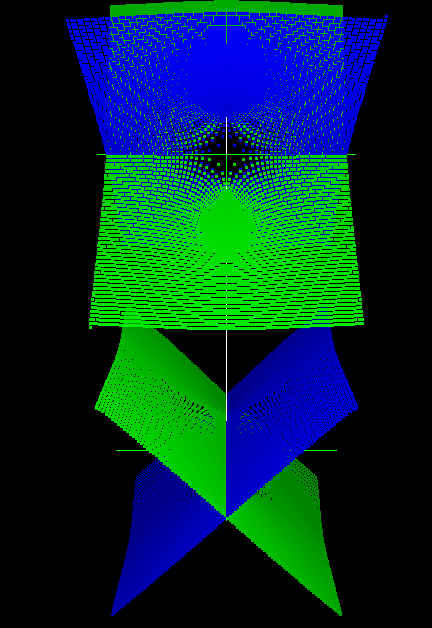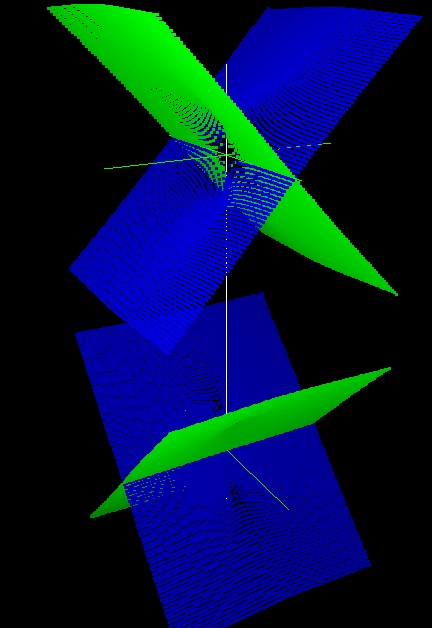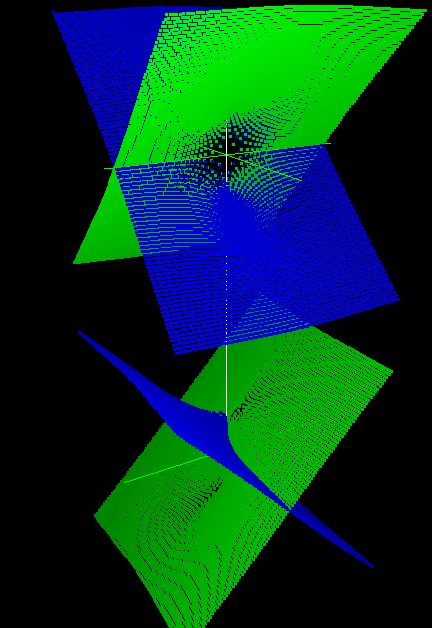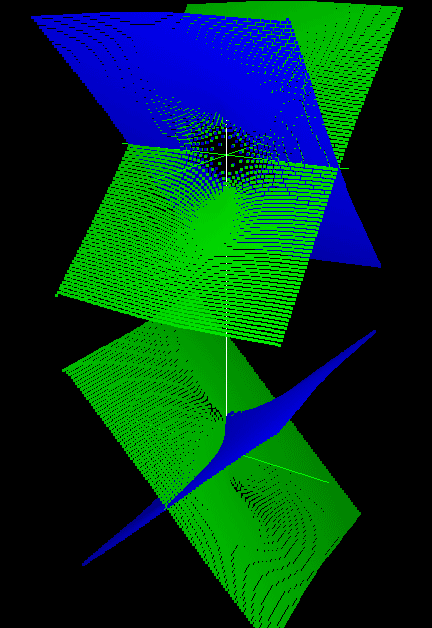
Уравнения конических кривых на комплексной плоскости и их ортогональных трехмерных проекций достаточно подробно рассмотрены в [19]. Рассмотрим подробнее вопросы наглядного моделирования окружности комплексной плоскости. В данной работе будем рассматривать только окружности с центром в начале координат. Они задаются следующим квадратным уравнением относительно переменных ẋ и ẏ: ẋ²+ẏ²–Ṙ²=0, где Ṙ=r+iṙ – радиус окружности, который может быть действительным (ṙ=0), нулевым (ṙ=r=0), чисто мнимым (r=0) и комплексным (ṙ≠0, r≠0).  На рис. 8 представлены перечисленные случаи.

а)                                                                                                              б)                                                                                               в)

г)                                                                                                              д)                                                                                               е)

Рис. 8. Модели отсеков окружностей комплексной плоскости:
а - проекции окружности с действительным радиусом на модели x_i-xOy-y_i, б - на модели y-xOx_i-y_i,
в - проекции окружности с нулевым радиусом на модели x_i-xOy-y_i, 
г - проекции окружности с чисто мнимым радиусом на модели x_i-xOy-y_i, д - на модели x-x_iOy_i-y,
е - проекции окружности с комплексным радиусом на модели x_i-xOy-y_i

Проекции окружности представляют собой двухлистные поверхности с горловиной (кроме окружности нулевого радиуса), которая представляет собой обыкновенную окружность в плоскости xOy для действительного радиуса или в плоскости x_iOy_i для чисто мнимого радиуса, горловина окружности с комплексным радиусом «повернута» относительно плоскостей xOy и x_iOy_i и, возможно, не является обыкновенной окружностью. На моделях также видны дополняющие окружность мнимые гиперболы в плоскостях x_iOy и xOy_i, которые проецируются без искажения.

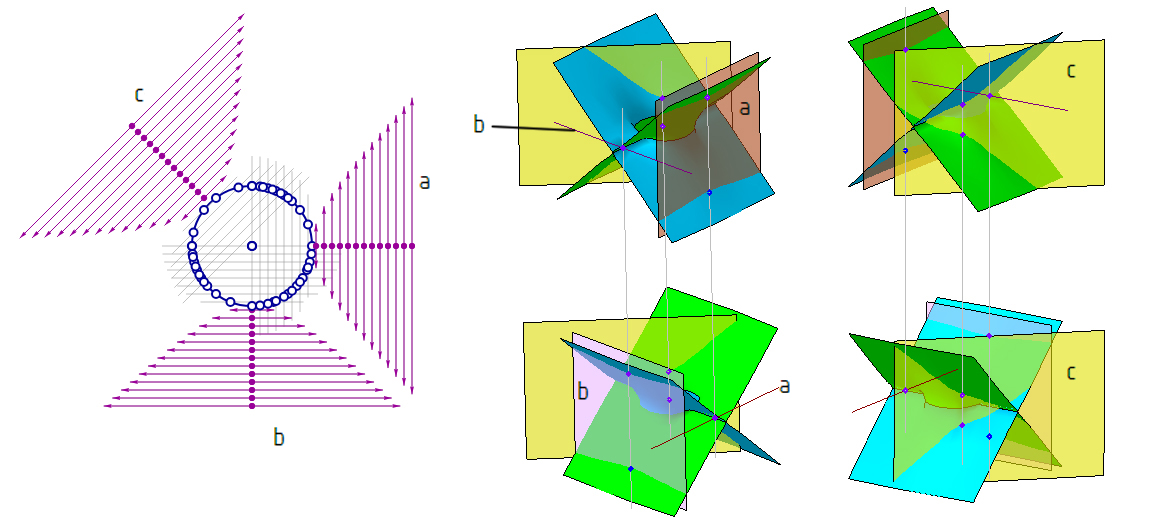
Трехмерные проекции позволяют получить наглядные модели отношений принадлежности и касания, соответственно, точки и прямой в области мнимого. На рис. 9, а показаны векторные чертежи мнимых точек пересечения действительной окружности с прямыми пучков вертикальных (a), горизонтальных (b) и наклонных прямых (c). Точки пересечения прямых пучка образуют мнимую гиперболу для каждого отдельного направления, имеется ∞¹ таких направлений. На рис. 9, б-в показаны модели пересечения окружности с горизонтальной (a), вертикальной (b) и наклонной (c) действительными прямыми такого пучка в мнимых точках. Точки пересечения при наличии трехмерных проекций прямой и окружности могут быть найдены конструктивно способом, приведенным в задаче 2. 

а)                                                                                                              б)                                                                                               в)

г)                                                                                                              д)                                                                                               е)

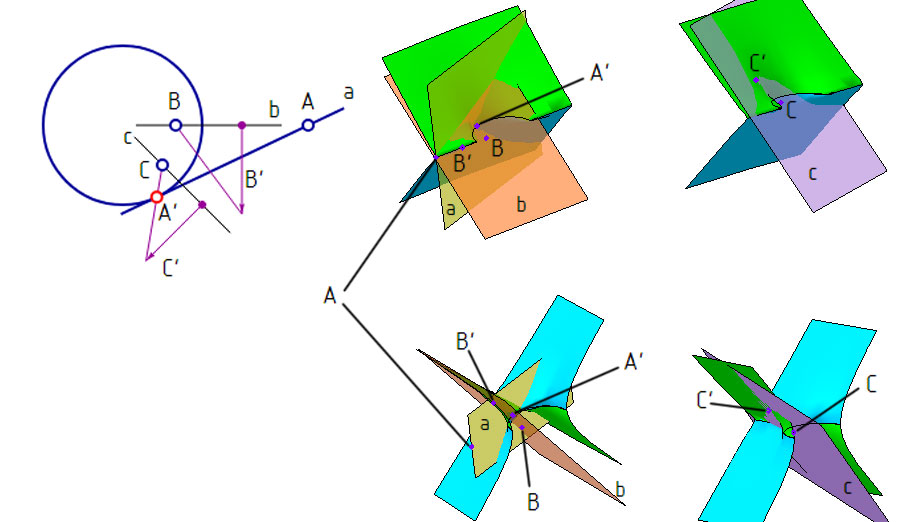
Рис. 9. Модели отсеков окружностей комплексной плоскости и отношений принадлежности и касания в системе «Компас-3D»

На рис. 9, г показан векторный чертеж касательных, проведенных к действительной окружности, из внешней точки A и внутренних точек B и C, и точек касания A', B' и C', соответственно. На рис. 9, д-е показаны модели касательных и точек касания в системе «Компас-3D». Из каждой пары касательных и точек касания показана только одна. Проекции окружности для наглядности рассечены. Мнимое продолжение в виде гиперболы отчетливо видно на срезе проекций поверхности. Прямые из внутренних точек проходят касательно к гиперболе соответствующего направления, которая на модели x_i-xOy-y_i проецируется без искажения только в плоскости xOx_i (верхняя проекция) и yOy_i (нижняя проекция).

Таким образом предлагаемая модель на основе трехмерных проекций позволяет наглядно представлять окружности комплексной плоскости, решать задачи принадлежности точки, взаимного пересечения и др. Представляет интерес дальнейшее исследование свойств окружностей с действительным и мнимым радиусом и других геометрических отношений и их трехмерных проекций.

Гиперболы и параболы комплексной плоскости

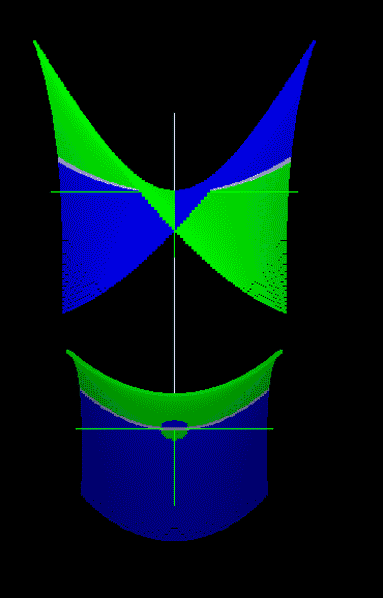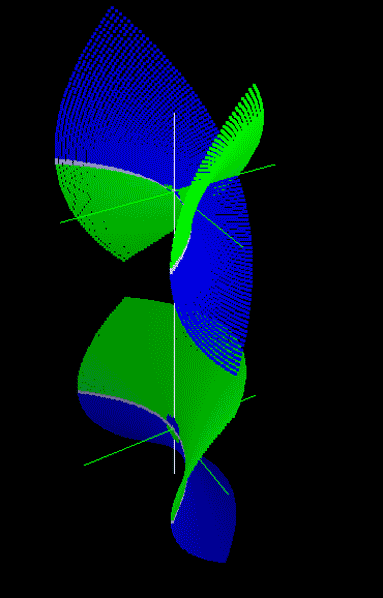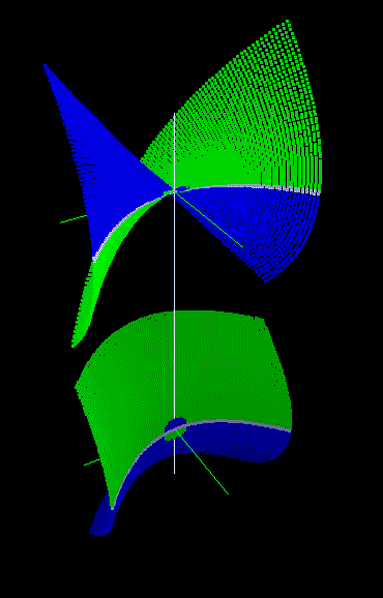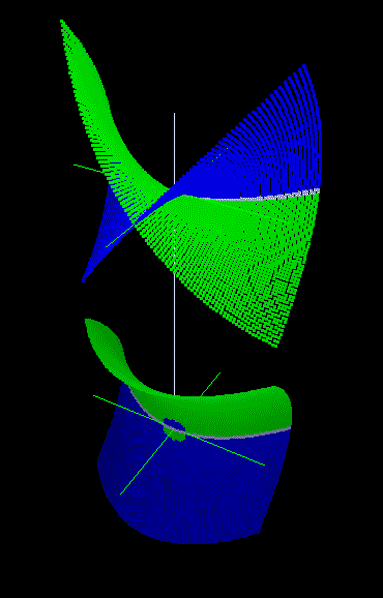
На рис. 10 показаны трехмерные проекции равнобочной гиперболы и параболы. На модели гиперболы видна дополняющая ее мнимая окружность и то, что изолированные ветви гиперболы в действительности связаны продолжениями кривой за пределами плоскости xOy и принадлежат обоим листам поверхности. Трехмерные проекции гиперболы напоминают проекции окружности, повернутой «на бок». Чтобы подтвердить или опровергнуть это предположение, требуются дополнительные исследования свойств геометрических преобразований поворота на комплексный угол на трехмерных моделях комплексной плоскости. 

а)                                                                                                              б)                                                                                               в)

г)                                                                                                                                                д)

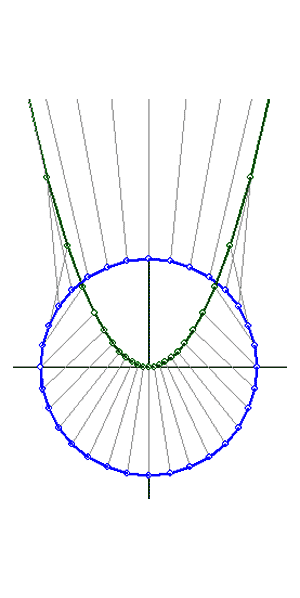
Рис. 10. Модели отсеков конических кривых комплексной плоскости:
а - проекции равнобочной гиперболы на модели x_i-xOy-y_i,
б - проекции отсека параболы комплексной плоскости на модели x_i-xOy-y_i, в - на модели y-xOx_i-y_i, 
г - преобразование параболы в окружность,
д - сравнение окружности и параболы в области соединения двух листов

В отличие от гиперболы, парабола не похожа на окружность, хотя также является двухлистной, Чтобы определить, какому листу принадлежит та или иная точка поверхности, был использован следующий подход. При помощи преобразования:

x' = 2px/(y+p), y' = (y-p)/(y+p)

парабола была преобразована в окружность (рис. 10, г) и при формировании точечного каркаса для каждой точки выполнялась проверка, какому листу окружности принадлежит соответствующая точка. На рис. 10, д показаны отсеки окружности и параболы для сравнения, на которых сходство соответствующих участков становится отчетливым. 

Программное обеспечение для представления фигур комплексной плоскости

Все плоские чертежи, в частности, векторные мнимых фигур были созданы при помощи интерпретатора геометрических команд, показанного в [17]. Для создания и отображения гиперэпюров использовались созданные программы на языке Delphi и JavaScript, имеющие в своем составе средства для вычислений с комплексными числами, а также библиотеки трехмерной графики OpenGL, WebGl и Three.JS.

Заключение

Было рассмотрено моделирование фигур комплексной плоскости при помощи двухкартинной трехмерной модели (гиперэпюра), получаемой путем ортогонального проецирования четырехмерного пространства, представляющего комплексную плоскость. Гиперэпюр позволяет моделировать двухмерные точечные многообразия (поверхности) четырехмерного пространства при помощи поверхностей трехмерного пространства. При этом сохраняются свойства непрерывности, инцидентности, касания, параллельности и др. Линии комплексной плоскости (прямые, кривые второго и высших порядков – окружности, гиперболы и др.) в представляющем ее четырехмерном пространстве моделируются именно двухмерными многообразиями, поэтому их модели на предлагаемом гиперэпюре оказываются наиболее наглядны. Гиперэпюры позволяют показать такие отношения, как пересечение и касание в мнимых точках, образование изолированных точек, ветвей и участков кривой и т. д.

Были рассмотрены модели прямых, выделены частные случаи (тип 0-3) и свойства их трехмерных проекций, показано решение задач о нахождении действительной точки мнимой прямой и пересечении двух прямых комплексной плоскости на гиперэпюре в системе «Компас-3D». Были показаны модели окружностей, гиперболы и параболы, пересечение окружности и прямых в мнимых точках и касание окружности и прямых в действительных и мнимых точках на гиперэпюре в системе «Компас-3D». Были показаны модели кубической параболы и кубического сплайна, в частности, тот факт, что непрерывность кусочных кривых нарушается за пределами действительной плоскости.

Был намечен ряд направлений для дальнейшего исследования – представляют интерес разработка конструктивных алгоритмов построения трехмерных проекций для прямых типа 3 и общего вида, исследование окружностей с комплексным значением радиуса, более подробное рассмотрение вопросов моделирования кривых второго порядка на гиперэпюре, а также свойств геометрических преобразований – в частности, поворота на произвольный (действительный или мнимый) угол и проективных (преобразование кривой второго порядка в окружность) и квадратичных (преобразование прямой в окружность), – на комплексной плоскости.

Список литературы

1. Гирш А.Г. Наглядная мнимая геометрия. – М.: ООО «ИПЦ "Маска"», 2008 – 216 с.
2. Иванов Г.С. О задачах начертательной геометрии с мнимыми решениями / Г. С. Иванов, И. М. Дмитриева // Геометрия и графика. – 2015. – Т. 3. № 2. – С. 3–8.
3. Волошинов Д.В. Визуально-графическое проектирование единой конструктивной модели для решения аналогов задачи Аполлония с учетом мнимых геометрических образов / Д.В. Волошинов // Геометрия и графика. – 2018. – Т. 6. № 2. – С. 23–46.
4. Коростелев Б.В. Инверсии кривых второго порядка как контуры аэродинамических профилей // Труды Центрального аэрогидродинамического института им. проф. Н. Е. Жуковского. – М.: НКТП СССР Главное управление авиационной промышленности, 1934. – Вып. 181. – С. 72.
5. Короткий В.А. Компьютерная визуализация кривой второго порядка, проходящей через мнимые точки и касающейся мнимых прямых // Научная визуализация. – 2018. – Т. 10, №1. – С. 56–68.
6. Пеклич В.А. Мнимая начертательная геометрия. – М.: АСВ, 2007. – 104 с.
7. Филиппов П.В. Начертательная геометрия многомерного пространства и ее приложения. – Л.: Изд-во Ленингр. ун-та, 1979. – 280 с.
8. Графский О.А., Пономарчук Ю. В., Холодилов А. А. Геометрия электростатических полей // Геометрия и графика. – 2018. – №. 1. – С. 10-19. – DOI: https://doi.org/10.12737/article_5ad085a6d75bb5.99078854
9. Короткий В.А. Линейная конгруэнция с мнимыми осями [Электронный ресурс]. – URL: http://dgng.pstu.ru/conf2019/papers/50 (Дата обращения: 25.03.2019)
10. Гирш А.Г., Короткий В.А. Мнимые точки в декартовой системе координат [Электронный ресурс]. – URL: http://dgng.pstu.ru/conf2019/papers/24 (Дата обращения: 25.03.2019)
11. Гирш А.Г. Точка, прямая, прямой угол и биссектриса в области мнимого  [Электронный ресурс]. – URL: http://dgng.pstu.ru/conf2019/papers/18 (Дата обращения: 25.03.2019)
12. Волошинов Д.В. Геометрическая лаборатория. Закладываем основы / Д.В. Волошинов / Качество графической подготовки: проблемы, традиции и инновации: Материалы VII Международной интернет-конференции КГП-2017. — URL: http://dgng.pstu.ru/conf2017/papers/53/
13. Волошинов Д.В. Геометрическая лаборатория. Инструменты ортогональности / Д.В. Волошинов / Качество графической подготовки: проблемы, традиции и инновации: Материалы VII Международной интернет-конференции КГП-2017. — URL: http://dgng.pstu.ru/conf2017/papers/72/
14. Бойков А.А. О построении моделей объектов пространства четырех и более измерений в учебном процессе // Геометрия и графика. – 2018. – Т. 6, № 4. – С. 54–71. – DOI: 10.12737/article_5c21f96dce5de8.36096061 (Краткий вариант в виде доклада на КГП-2017 http://dgng.pstu.ru/conf2017/papers/57/).
15. Бойков А.А. Трехмерная визуализация геометрических образов и отношений комплексной плоскости / А.А. Бойков, Д.А. Шулайкин // Проблемы координации работы технических вузов в области повышения качества инженерно-графической подготовки студентов (с. Дивноморское, 10-16 сентября 2018 г.). – Ростов-на-Дону: ДГТУ, 2018. – С. 163–171.
16. Графский О.А. Теоретико-конструктивные проблемы моделирования мнимых элементов в начертательной геометрии и ее приложения: Дисс. ... д-ра техн. наук — 05.01.01. – М., 2004. – 409 с.
17. Бойков А.А. Средства автоматизации геометрических построений // Двенадцатая международная научно-техническая конференция студентов, аспирантов и молодых ученых «Энергия-2017»: Материалы конференции. Т.5. – Иваново, 2017. – С. 188-189.
18. Янке Е., Эмде Ф., Леш Ф. Специальные функции. Формулы, графики, таблицы. – М.: Наука, 1964. – 344 с.
19. Конакбаев, К.К. О мнимых точках пересечения прямой с коникой / К.К. Конакбаев // Кибернетика графики и прикладная геометрия поверхностей: Труды МАИ. - М., 1970. - №205. - Вып. 4. - С. 33-42.
20. Гирш А. Г. Уравнения первой и второй степени с комплексными коэффициентами и их графики / А. Г. Гирш // Геометрическое моделирование в практике решения инженерных задач. – Омск: ОмПИ, 1991. – С. 79–85

Гирш Антон Георгиевич (29 марта 2019 г. 0:12)	Уважаемые авторы Алексей Александрович и Дмитрий Алексеевич, замутили Вы, однако, тему. Пока ничего определённого сказать не могу кроме того, что непривычно. Вы разрушаете картину целостной фигуры тем, что разлагаете её по параметрам, которыми в дальнейшем варьируете. Т.е. вообразить геометрию фигуры невозможно, возможно только следить за логикой. Есть вопрос: что такое окружность с комплексным радиусом? Может ли она появиться в результате какой-либо геометрической операции? Это двумерная фигура или трёхмерная? С уважением, Антон Г. Гирш.
Селиверстов Александр Владиславович (29 марта 2019 г. 2:42)	Здравствуйте, Алексей Александрович и Дмитрий Алексеевич. Жалко, что интересные доклады появляются так поздно. Но позвольте добавить ещё несколько вопросов или замечаний в последний день конференции.  0) Видимо "комплексная окружность" соответствует двумерной вещественной поверхности, вложенной в четырёхмерное пространство, причём эта поверхность служит пересечением двух трёхмерных вещественных квадрик. 1) На рис. 8–10 самопересечение возникло в результате проекции на трёхмерное пространство или же особенность присуща исходной поверхности в четырёхмерном пространстве? 2) Хотелось бы перекинуть мостик к другим исследованиям. Пересечения вещественных квадрик рассмотрены, например, в статье: В.А. Краснов, “О пересечениях двух вещественных квадрик”, Изв. РАН. Сер. матем., 82:1 (2018), 97–150. Можно ли сопоставить результаты у Вас и в той работе? 3) При решении задачи 2 бессмысленно указывать результат вычислений одним методом с точностью, превышающей точность другого метода. С уважением, А.В. Селиверстов
Бойков Алексей Александрович (29 марта 2019 г. 11:56)	Здравствуйте, Антон Георгиевич! Спасибо за внимание к нашему докладу. Окружность с комплексным радиусом у нас получается в общем случае, если задать ее тремя произвольными (не сопряженными) точками с комплексными координатами. Например, берем три точки: A = [P 60 + 60i, 60 + 60i], B = [P -50 + 50i, 50 - 50i], C = [P -50i, 50i] Вычислительная процедура, работающая по обычным формулам для действительной окружности, но с внутренней поддержкой комплексных вычислений определяет центр и радиус: o=c3p(A,B,C) o = [x = 25.833333333333332 + 30i, y = 75.83333333333333 + 30i, r = 19.77977285674572 + 27.806183821389418i] При подстановке координат исходных точек в уравнение x2+y2-r2=0, получаем тождество, то есть исходные точки принадлежат такой окружности. Для сравнения - проекция окружности с действительным (слева) и комплексным (справа) радиусом в пространство xi-xOy: По поводу размерности фигуры вопрос не совсем понятен. Любая линия, задаваемая уравнением типа F(x,y)=0 на комплексной плоскости, представляет собой точечное множество ∞2, то есть поверхность.в обычном понимании этого слова. Поскольку каждая точка двухмерной комплексной пл-ти имеет 4 степени свободы (x, xi, y, yi), то двухмерная комплексная плоскость, фактически, есть 4-мерное пространство, в котором лежат эти поверхности. Причем эти поверхности, в общем случае, искривлены так, что не могут лежить ни в одном трехмерном подпространстве полностью (по аналогии с пространственными кривыми, которые "не имеют натуральной величины" на плоскости, эти - не имеют натуральной величины в трехмерном пространстве и всегда проецируются в трехмерное пространство с искажением). с уважением, А.Бойков
Волошинов Денис Вячеславович (29 марта 2019 г. 14:12)	Здравствуйте, Алексей Александрович и Дмитрий Алексеевич! Спасибо за интересный доклад! Впервые с  окружностями с мнимым центром и мнимым радиусом мне довелось столкнуться при общем решении задачи Аполлония, в том числе и в многомерном случае. Честно признаюсь, многие вещи выглядели очень необычно, непонятно было, как все это связать с проективной плоскостью, как работать с объектами мнимой природы в рамках информационной среды. Но через некоторое время стало ясно, что все здесь находится в совершенном единстве и алгоритмы, привычные по действительным аналогам, работают здесь точно так же! Именно поэтому средства моделирования просто обязаны представлять такие объекты, визуализировать их, включать во взаимодействие с другими геометрическими образами! Здесь необъятный простор для исследований, фантазии и творчества. От души желаю Вам успеха и побед на этом пути! С уважением, Д. Волошинов
Бойков Алексей Александрович (29 марта 2019 г. 18:55)	Александр Владиславович, спасибо за внимание к докладу и ценные замечания! Статья В.А. Краснова в настоящий момент не доступна, обязательно почитаю. Насчет п. 1. Самопересечение, похоже, возникает при проецировании. Если рассматривать пересечение действительной окружности с ∞1 пучками параллельных прямых, всякий раз получаем мнимое продолжение в виде гиперболы. То есть имеется что-то вроде гиперболоида вращения, но каждый меридиан такого гиперболоида дополнительно повернут вокруг действительной плоскости, так что при проецировании в какое-либо пространство одна из ∞1 гипербол сжимается в пару двойных лучей, отчего возникает самопересечение. с уважением, А.Бойков
Бойков Алексей Александрович (29 марта 2019 г. 20:07)	Здравствуйте, Денис Вячеславович! Спасибо за высокую оценку. Ваши эксперименты в Симплексе с инверсиями относительно мнимых окружностей и статьи Антона Георгиевича не давали покоя, хотелось увидеть все эти "мнимые" фигуры. И, кажется, что-то в этом направлении стало получаться. с уважением, А.Бойков