ТОРСОВАЯ ПОВЕРХНОСТЬ В КУРСЕ НАЧЕРТАТЕЛЬНОЙ ГЕОМЕТРИИ

|
Короткий Виктор Анатольевич | (Южно-уральский государственный университет (Национальный Исследовательский Университет)) |
Аннотация
Рассматриваются некоторые вопросы формообразования торсовой поверхности
Ключевые слова: Бесконечно близкие образующие, стрикционная линия
При изучении торсовой поверхности у учащихся возникают вопросы, связанные как с ее формообразованием, так и со свойством развертываемости. Учебник предлагает определение торса как поверхности, образованной движением касательной к пространственной кривой. Но нетрудно смоделировать линейчатую развертываемую поверхность иным способом. Возьмем две произвольные кривые или поверхности, жестко связанные между собой, поставим их на плоскость и осуществим качение. В общем случае наша конструкция касается плоскости в двух точках. Соединяя точки касания прямолинейными образующими, получаем линейчатую поверхность. Посредством качения она развертывается на плоскость, следовательно, это торс.
Возьмем в качестве направляющих две пространственные кривые a и b. Произвольную точку A на одной из них (например, на a) примем за вершину конуса с направляющей b. Построим плоскость Σ, проходящую через касательную tА к направляющей a и касающуюся конуса (рис. 1). В точке B плоскость Σ касается направляющей b. Очевидно, касательная tB лежит в плоскости Σ. Линия касания AB дает образующую торса. Всякой точке одной из направляющих ставится в соответствие единственная образующая (особые случаи, когда плоскость Σ не касается кривой b или касается ее в двух и более точках – исключаем из рассмотрения).
В частности, если направляющие a и b совпадают, получаем определение торса как поверхности касательных. В качестве другого известного частного случая отметим поверхность одинакового наклона, когда вершина направляющего конуса движется по пространственной кривой (кромке откоса), а откос (торсовая поверхность) формируется как огибающая множества последовательных положений конуса.
Таким образом, принятое в учебной литературе определение торса как регулюса, выделенного из конгруэнции бисекант условием совпадения двух точек пересечения – лишь частный случай общего определения торса как развертываемой на плоскость линейчатой поверхности с двумя образующими.
Но и это определение нельзя считать исчерпывающим. Следует объяснить, что торс – это поверхность, огибающая любое однопараметрическое множество плоскостей. Например, определяя торс одной направляющей, мы фактически задаем однопараметрическое множество соприкасающихся плоскостей этой направляющей (в качестве параметра – расстояние вдоль кривой).
Определив торс как поверхность, касательную к однопараметрическому семейству плоскостей, нам придется показать учащимся два существенных свойства этой поверхности – развертываемость и наличие ребра возврата, которого касаются все образующие торса. Заметим, что постоянство касательной плоскости вдоль образующей следует непосредственно из принятого определения.
Для иллюстрации основных свойств торса построим произвольную гранную поверхность, образованную касательными плоскостями (рис. 2). Торс задан направляющими a и b, а касательные плоскости определены в соответствии с вышеописанным алгоритмом. Грани полученной поверхности пересекаются по пространственной ломаной ABC… Если неограниченно сближать касательные плоскости, то их линии пересечения в пределе становятся образующими торса. Например, если точки 1 и 3 стремятся к точке 2 (здесь 1, 2, 3 – точки касания граней с образующей a), то ребра m и n становятся двумя бесконечно близкими образующими торса, а точки B и C – бесконечно близкими точками ребра возврата. Образующие торса являются касательными к ребру возврата, так как всякая образующая проходит через две его бесконечно близкие точки. Так, ребро m, стремясь занять положение образующей, проходит через бесконечно близкие точки B и C. Заметим также, что в процессе предельного перехода соседние ребра m и n остаются лежащими в одной плоскости, следовательно, две бесконечно близкие образующие пересекаются, что доказывает развертываемость торса.
Таким образом, к основным свойствам торса легко прийти, заменяя его гранной поверхностью – с последующим предельным переходом. Но этот переход в сознании учащегося связан с серьезным психологическим барьером, неизбежно возникающим у всякого, кто впервые встречается с анализом бесконечно малых. Действительно, здравый смысл подсказывает, что две сколь угодно близкие касательные к пространственной кривой не могут пересекаться. Они скрещиваются. Понятно, что расстояние между бесконечно близкими касательными стремится к нулю. Но ведь у любой косой линейчатой поверхности, как и у торса, расстояние между бесконечно близкими образующими бесконечно мало, причем также имеется линия сжатия – аналог ребра возврата торса. Это еще более затрудняет понимание особых дифференциальных свойств торсовой поверхности, отличающих ее от других поверхностей. Поэтому следует временно отказаться от наглядных геометрических образов и сравнить численные значения некоторых локальных параметров торса и косой поверхности.
Через две бесконечно близкие точки A и B, лежащие на линии сжатия (стрикционной линии) d линейчатой поверхности, проходят две образующие m и n (рис. 3). Определим бесконечно малое расстояние δ=A'B' между образующими в зависимости от расстояния l=AB. Отрезок A'B' получен ортогональным проецированием отрезка AB на направление общего перпендикуляра соседних образующих, поэтому A'B'=ABsinα, где α – угол между образующей и линией сжатия. Следовательно, в любой точке линии сжатия имеем δ/l= sinα. В частности, для торса линия сжатия вырождается в ребро возврата, которого касаются все образующие (α=0), и параметр δ/l равен нулю. Этот параметр можно трактовать как производную некоторой функции δ=f(l) при l=0. Равенство производной нулю означает, что при l=0 бесконечно малое приращение dl расстояния l между точками касания не приводит к изменению расстояния δ между бесконечно близкими касательными; это расстояние остается равным нулю, то есть бесконечно близкие касательные (образующие торса) пересекаются. Образующие косой линейчатой поверхности в общем случае пересекают линию сжатия под произвольным углом α, поэтому то же самое рассуждение приводит нас к выводу, что бесконечно близкие образующие косой поверхности – скрещиваются.
Рассмотрим еще одну дифференциальную характеристику: параметр распределения p= δ/φ, где δ и φ – расстояние и угол между соседними бесконечно близкими образующими. Известно [Выгодский М.Я. Дифференциальная геометрия], что для любой поверхности касательных, кроме цилиндрической, этот параметр тождественно равен нулю. Что это означает? Параметр p считаем производной dδ/dφ при φ=0, то есть при совпадающих образующих. Возьмем две совпадающие образующие торса и повернем одну из них на бесконечно малый угол dφ. Соответствующее приращение dδ расстояния между образующими равно нулю. Но в начальный момент образующие совпадали. Следовательно, соседние бесконечно близкие образующие, угол φ между которыми бесконечно мал, лежат в одной плоскости.
Покажем, что у любой косой поверхности параметр распределения отличен от нуля. Произвольная линейчатая поверхность в общем случае задается тремя криволинейными направляющими. Рассматривая бесконечно малые перемещения некоторой образующей, заменяем дуги направляющих касательными к ним. Иначе говоря, заменяем линейчатую поверхность соприкасающимся с ней вдоль исследуемой образующей однополостным гиперболоидом. Аффинным сжатием этот гиперболоид может быть преобразован в гиперболоид вращения. Очевидно, аффинное преобразование не может качественным образом изменить локальные свойства поверхности. Поэтому достаточно убедиться, что у гиперболоида вращения параметр распределения не равен нулю. На рис. 4 показаны стрикционная линия (горловое сечение) d, направляющий конус и две образующие m, n гиперболоида вращения. Расстояние δ между соседними образующими равно ABsinα (см. рис. 3), где α – угол наклона образующих к плоскости горлового сечения. При малом ω имеем δ=Rωsinα, где R– радиус горлового сечения, ω – угол между радиус-векторами OA и OB.
Отметим на направляющем конусе прямые m' и n', параллельные образующим m, n. Угол φ между ними определим из треугольника OA'B' (см. рис. 4). Принимая высоту направляющего конуса равной единице, получаем при малом ω: A'B'=ωctgα, а угол φ= ωcos α, следовательно, параметр распределения гиперболоида вращения равен p= δ/φ=Rtgα. При аффинном растяжении параметр p становится переменным, но принять нулевое значение он сможет только на некоторых образующих, которые касаются линии сжатия. У торса параметр распределения тождественно равен нулю, так как все его образующие касаются ребра возврата (линии сжатия).
Итак, соседние бесконечно близкие образующие торса пересекаются. Еще раз отметим, что этот факт труден для непосредственного восприятия, поскольку наша геометрическая интуиция трактует понятие “бесконечно близкие” точки или образующие как “очень близкие”, невольно заменяя функцию (переменную величину, стремящуюся к нулю) очень малой постоянной величиной. Поэтому следует объяснить учащемуся, что речь идет о сравнении бесконечно малых величин: расстояние δ между бесконечно близкими касательными к пространственной кривой имеет высший (в общем случае – третий) порядок малости относительно расстояния l между точками касания. Для любой другой линейчатой поверхности бесконечно малые величины δ и l – одного порядка малости. Только это мы имеем в виду, утверждая, что бесконечно близкие образующие торса пересекаются, а образующие косой поверхности – скрещиваются.
Заключение. Остаются не рассмотренными еще два вопроса, один из которых связан с формообразованием торса посредством выделения его из конгруэнции бисекант. Даны две совпадающие пространственные кривые m=m', на которых отмечен ряд точек 1=1', 2=2', 3=3', 4=4',… Выполним плоско-параллельный перенос одной из кривых по произвольному направлению u. Соединяя соответственные точки 1-1', 2-2',… прямыми линиями, получим цилиндрическую поверхность, то есть поверхность с направляющими m, m' и третьей направляющей, выродившейся в несобственную точку U направления переноса u. Процесс обратного переноса кривых m, m' до их совмещения следует рассматривать как предельный переход, в процессе которого пределом несобственной точки U является однопараметрическое множество несобственных точек всех касательных к кривой m=m', то есть некоторая несобственная кривая w, которую и следует считать третьей направляющей торсовой поверхности. Кривая w является линией пересечения торса с несобственной плоскостью. Проблема заключается в восприятии, понимании и строгом математическом описании этого неуловимого момента, когда несобственная точка U расширяется до однопараметрического множества точек. Привычное преподавателям начертательной геометрии “вырождение” линии в точку заменяется в рассматриваемом примере “расширением” точки в линию.
Другой вопрос связан с исследованием случая, когда одна из кривых m=m' с указанными на них точками 1=1', 2=2',… подвергается произвольному ( не плоскопараллельному) переносу, после чего соответственные точки соединяются прямыми линиями. Получаем линейчатую поверхность, заданную инженерным способом. Поверхность имеет всего две явно указанные направляющие m и m', и дополнительное словесное указание на взаимно-однозначное соответствие, установленное между рядами точек 1, 2, 3,… и 1', 2', 3,… на этих кривых. Возможно ли словесный алгоритм формирования поверхности “заменить” эквивалентным указанием третьей направляющей? И есть ли она, третья направляющая?
Рисунки к докладу
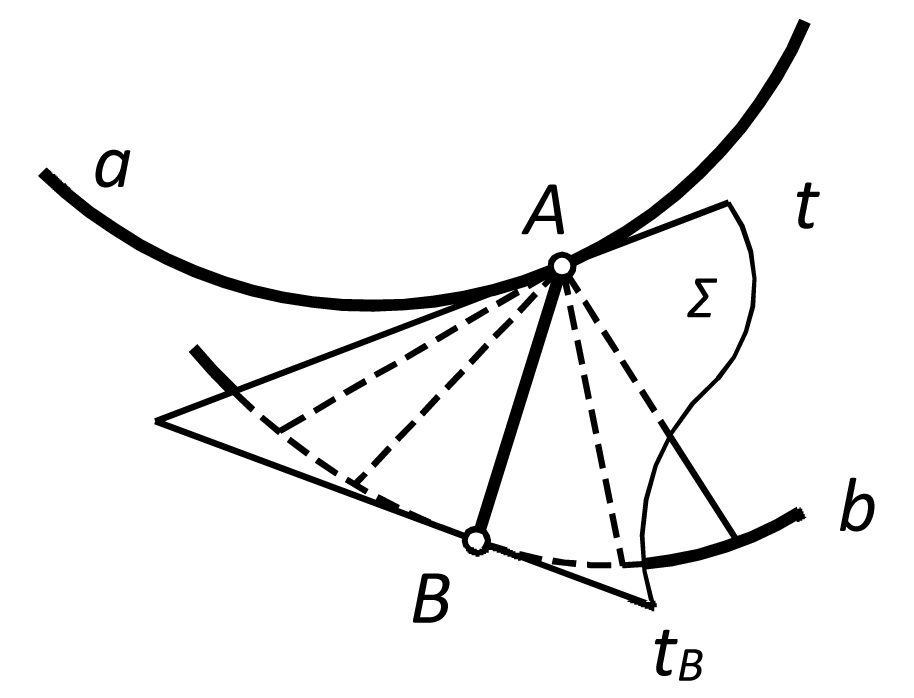
Рис. 1 Схема формирования торсовой поверхности
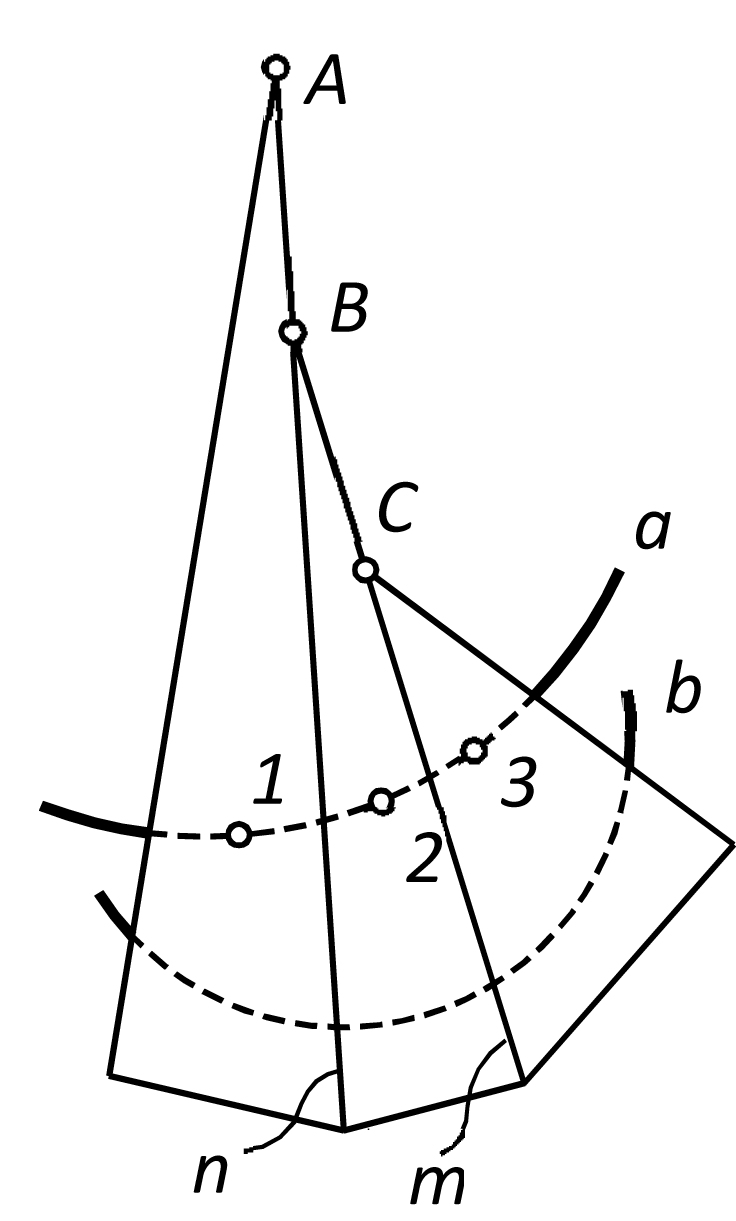
Рис. 2 Торс как предел многогранника
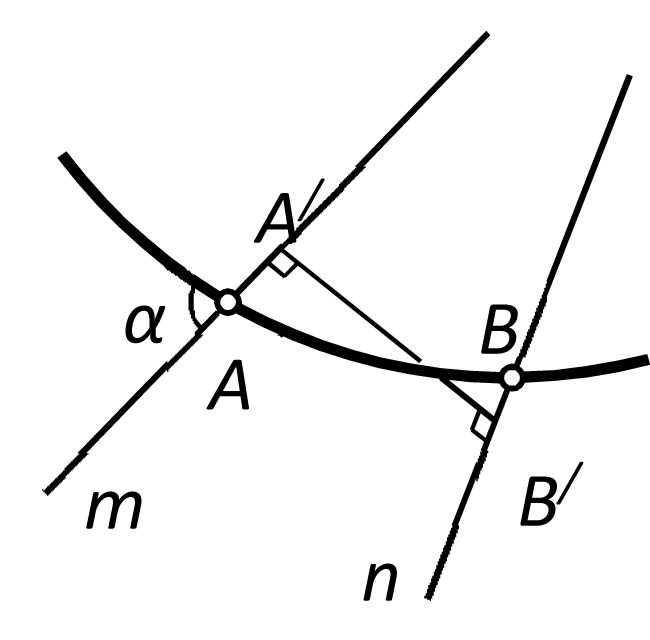
Рис. 3 Стрикционная линия линейчатой поверхности
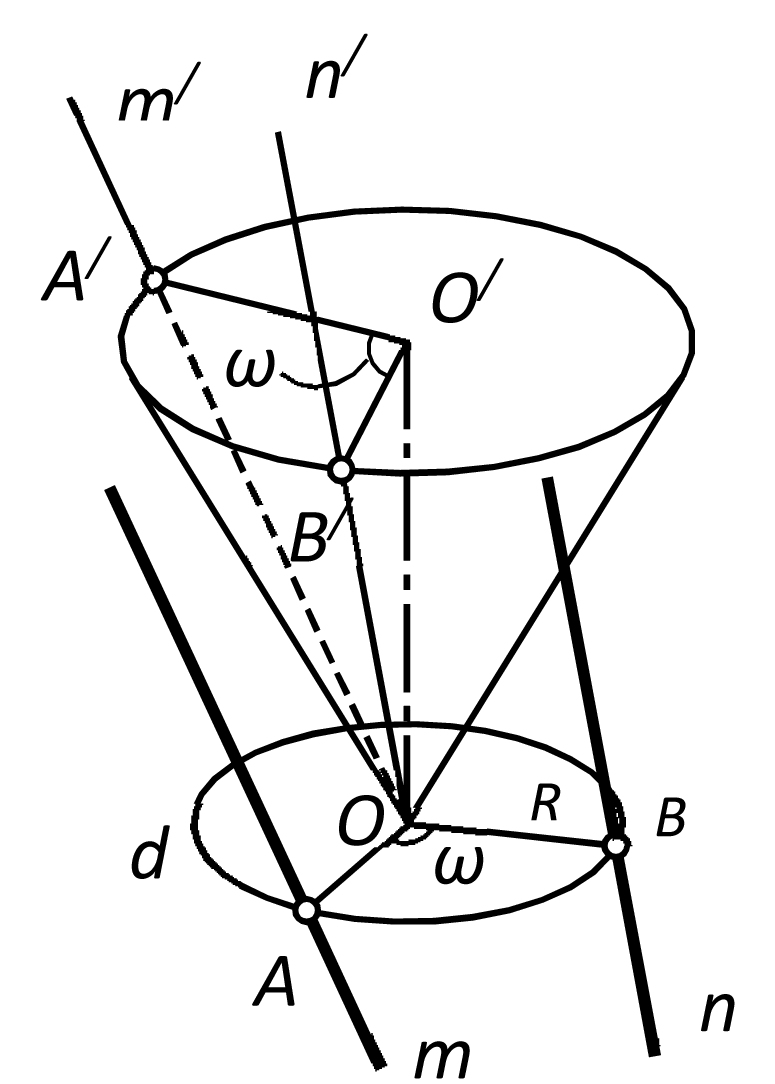
Рис. 4 Параметр распределения гиперболоида вращения
Вопросы и комментарии к выступлению:

Сальков Николай Андреевич (17 марта 2019 г. 14:09) |
Здравствуйте, Виктор Анатольевич! Ваш пример с двумя линиями (или поверхностями) и касательными к ним ∞1 плоскостей доказывает, что мое утверждение о том, что для ЛП необходимы три направляющие, верно. Третьей направляющей является перемещающаяся плоскость. При этом если одга плоскость должна фиксировать 2 параметра у образующей (как это, в общем-то и происходит), то переменное положение плоскости освобождает один параметр. В результате имеем следующее: касание образующей прямой с двумя поверхностями или ее пересечение с двумя кривыми фиксирует 2 параметра из ∞4 прямых. А ∞1 плоскостей, содержащее образующую, фиксируют 1 параметр образующей. Таким образом, из ∞4 прямых получаем ∞1 прямых - линейчатую поверхность. Насчет ∞1 плоскостей, которое составляют торс. Чтобы получить ∞1 плоскостей, необходимо зафиксировать 2 параметра из трех. Это может случиться при касании плоскости двух линий или двух поверхностей - это если мы рассматриваем задание торса именно с геометрической точки зрения. Таким образом, снова получаем три направляющие: две геометрические фигуры и ∞1 плоскостей. По поводу инженерного задания. Две кривые, которые пересекает образующая, фиксируют два параметра у ∞4 прямых. Вопрос: каким образом для создания поверхности из ∞4 прямых фиксируется еще 1 параметр? Очевидно, что здесь присутствует третья направляющая в неявном виде. С уважением, Н.А. Сальков |

Короткий Виктор Анатольевич (17 марта 2019 г. 14:44) |
Николай Андреевич, добрый день! Кажется, я понял, в чем дело. Вопрос, заданный в заключительном абзаце статьи, сильно отдает казуистикой. Действительно, пусть между двумя криволинейными направляющими a, b установлено взаимно-однозначное точечное соответствие w (не важно, каким способом). Соединяя соответственные точки, получаем линейчатую поверхность с двумя направляющими a, b. В сечении этой поврхности произвольной плоскостью получим кривую q. Теперь можно спокойно вообще забыть о заданном ранее соответствии w, потому что имеем линейчатую поверхность с тремя направляющими a, b, q, тождественную поверхности, заданной направляющими a, b и функцией w. Прошу прощения за необдуманный абзац. С уважением, В. Короткий
|

Сальков Николай Андреевич (17 марта 2019 г. 17:46) |
Виктор Анатольевич, а я Вас благодарю за столь полное представление задания торса! С уважением, Н. Сальков |
Назад Go Back