ВЕРИФИЦИРУЕМОСТЬ ИНЖЕНЕРНО-ГРАФИЧЕСКИХ ЗАДАЧ КАК НЕОБХОДИМОЕ УСЛОВИЕ ЭФФЕКТИВНОЙ САМОСТОЯТЕЛЬНОЙ РАБОТЫ

В статье анализируются вопросы самостоятельной проверки инженерно-графических задач студентами. Вводится понятие верифицируемости, как практическая доступность самостоятельной проверки задач студентами при поддержке компьютерных систем. Формулируются группы задач верификации. Показывается применение геометро-графических тренажеров для самостоятельной проверки элементарных приемов проекционного моделирования.

Введение

В своей деятельности специалисты-инженеры повсеместно имеют дело с геометрическими моделями. Геометро-графическая среда является основой особого рода коммуникаций [1], которой принадлежат 92% инженерной деятельности, включая геометрическое моделирование и документирование, моделирование технологических процессов, функциональный дизайн, инженерный анализ. В этой коммуникационной среде геометрические модели выполняют роль языка с его особыми правилами и функциями. Этому языку свойственны особая точность и ясность при передаче инженерных сведений. Все это объясняет разнообразие геометрических моделей, с которыми встречаются студенты инженерных специальностей.

В соответствии с государственной программой РФ «Развитие образования» на 2013-2020 гг, модернизация учебных программ должна обеспечивать «гибкость и индивидуализацию процесса обучения» и направлена «на повышение самостоятельной учебной деятельности студентов» (Основное мероприятие П.1.6, в [2, С. 109]). Это предполагает «интенсификацию всех уровней учебно-воспитательного процесса» [3] и создание условий для формирования «психологической установки на самостоятельное систематическое пополнение знаний и овладение умениями ориентироваться в потоке научной информации» [4].

В отношении анализа и синтеза геометрических моделей успешная самостоятельная деятельность возможна лишь в условиях оперативной верификации ее результатов. Верификация — это процесс и результат проверки, верно или неверно построена та или иная тренировочная модель, и какие допущены ошибки. Очевидно, компьютерные системы являются ключевым звеном в организации оперативной верификации геометро-графических моделей в самостоятельной работе студентов.

Как известно, проверка в условиях автоматизации обучения может выполняться в двух формах [5]: в форме ручной проверки (в частности, самопроверки) и в форме автоматизированной проверки. Если исключить из рассмотрения функции контроля обучения (расчет оценок и обратную связь с процессом обучения), тогда всякая автоматизированная проверка — наиболее автоматизированный вариант самопроверки.

Верификацией задач дисциплины будем называть организацию самостоятельной проверки их при поддержке компьютерной системы (в том числе полностью автоматическую проверку правильности решений). Верифицируемостью задач дисциплины будем называть практическую доступность их верификации.

В настоящей работе мы попытаемся найти ответы на следующие вопросы:

1) что составляет основу самостоятельной проверки решений геометро-графических задач;

2) какие задачи стоят перед компьютерной системой верификации;

2) как компьютерные системы обеспечивают верификацию;

3) как может быть организована верификация решений геометро-графических задач.

Теоретические основы самостоятельной проверки геометро-графических работ

В книге Б. И. Аргунова и М. Б. Балка, посвященной построениям на плоскости [6], дается определение задачи на построение, для решения которой «требуется построить … некоторую фигуру, если дана некоторая другая фигура и указаны некоторые соотношения между элементами искомой фигуры и элементами данной фигуры». Рассматривается схема решения, которая включает: 1) анализ, 2) построение, 3) доказательство, 4) исследование.

Такая же схема приводится в книге В. В. Глоговского [7], посвященной задачам начертательной геометрии и геометрического моделирования: вводится понятие «конструктивной задачи» и ее «степени» (степень уравнения, к которому приводится ее аналитическое решение), перечисляются «средства построения» (линейка, циркуль, угольник и др.). Задачи различных степеней относятся к тем или иным средствам.

Этап доказательства включает формальную проверку, что построенная фигура соответствует всем указанным условиям, исследования — включает постановку и ответ на дополнительные вопросы: является ли полученное решение частным или общим, всегда ли оно применимо, каким другим способом можно решить задачу, как решить задачу в более общей постановке и т. д. Доказательство и исследование призваны обеспечить проверку правильности и поиск иных методов решения.

Основными средствами интенсификации обучения инженерно-графическим дисциплинам, кроме применения САПР (см. ниже), являются пошаговые демонстрации [8], тестирование [9, 10, 11 и др.], электронные учебники, видеоматериалы и т. п. [12, 13 и др.]. Все перечисленные технологии, кроме тестирования, осуществляют представление информации, а не контроль.

В работах [14, 15] выделяются четыре уровня овладения материалом: 1) знакомство — общее представление об объекте изучения, студент способен лишь опознавать и различать объекты изучения в ряду им подобных; 2) понимание — усвоение основных понятий, развитие способностей судить об особенностях предметов, давать характеристику, воспроизводить по памяти усвоенную информацию; 3) умение — способность применять усвоенную информацию при решении задач в той мере, которая не требует ее преобразования; 4) навык — способность решать любые задачи, овладение информацией в той степени, чтобы без труда преобразовывать ее и переносить приобретенные умения.

Если обратиться к определению задачи на построение (см. выше), то становится очевидным, что самостоятельная проверка студентами собственных решений возможна только на уровнях «понимание» и «умение»: студент понимает, какие фигуры изображены, какими свойствами они обладают, и может проверить выполнение всех условий задачи.

Далее, в работе [14] отмечается, что «выборочные ответы … не обеспечивают обучения выше уровня «знакомство». Выборочные ответы — это широко внедряемые на всех уровнях современной системы образования тесты. Результатом этого внедрения в школьное образование можно считать низкий уровень подготовки первокурсников. Печально показателен на этом фоне учебник [16].

Таким образом, применяемые в инженерно-графическом образовании технологии в принципе не решают проблемы обеспечения верифицируемости.

Проблемы традиционного подхода к самостоятельной проверке геометро-графических задач

Особенностью курса начертательной геометрии в традиционном изложении (для примера были взяты учебники Н. Ф. Четверухина (1963), А. Д. Посвянского (1970), В. О. Гордона (1978), С. А. Фролова (1983)) является то, что в учебниках даются общие методы построения чертежей, приводятся примеры, но отсутствует методика проверки и самопроверки решений. Советское школьное образование было достаточным для того, чтобы студентам были очевидны как методы решения задач, так и способы проверки решений. Так, в сборнике задач С. А. Фролова (1986) [17] отмечается, что «графические способы решения обладают … свойством, что … на любом этапе решения можно контролировать правильность их выполнения».

Через 30 лет оказывается, что это не вполне справедливо. По прежнему «в основе контроля лежат инвариантные свойства параллельного проецирования и теоремы начертательной геометрии, планиметрии и стереометрии» [17], которые остались неизменными, но обнаружилась иная проблема: привыкшие к «наглядности» (см. доклад Соколовой Л. С. «Геометрическая подготовка бакалавров в условиях ухода классического чертежа из современного высокотехнологичного производства») движущихся реалистичных картинок, они перестали понимать... как можно рисовать (курсивом даны слова, употребляемые студентами) две и три точки или прямые, а подразумевать при этом одну, и делать какие-то выводы о ее свойствах; как можно рисовать прямую k₁, а подразумевать какую-то прямую k, которой даже нет на рисунке. Они честно учат и выучивают «свойства проецирования» и некоторые теоремы, но не могут взять в толк, какое отношение все это имеет к точкам и палочкам, которые зачем-то надо называть «проекциями». При всяком удобном случае они воспроизводят с образца вместо самостоятельного решения, и вообще по возможности избегают умственной обработки информации. Например, вместо того, чтобы что-то перечертить, переписать или запомнить, используют фотокамеры мобильных телефонов.

В ходе бесед с отстающими студентами, в ходе наблюдения за тем, как студенты объясняют друг другу решение задач, в ходе проверки чертежей становится очевидным, что многие первокурсники:

1) Не тренируют абстрактно-логическое мышление и испытывают сложности с пониманием абстрактной информации, в частности:

- Не могут мыслить отвлеченно, не понимают формальных (не подкрепленных наглядностью) методов моделирования.

- Не умеют делать выводы и обобщать.

2) Не тренируют память и испытывают сложности с запоминанием.

Все это показывает, что формы самостоятельной проверки, характерные для традиционной формы преподавания инженерно-графических дисциплин, недостаточны, по крайней мере на начальных этапах освоения дисциплины.

Задачи системы верификации инженерно-графических задач

Становится очевидной необходимость обеспечить верифицируемость методов дисциплины в условиях низкой подготовки студентов.

Хочется отметить отдельно важность опыта применения формальных моделей.

Наглядность, долгое время служившая основой геометрического метода (можно вспомнить знаменитое «смотри» Ганеша в качестве доказательства), в конце концов уступила свое место формальному взгляду: геометрия, как математическая наука, не связана с образами (точками, прямыми), в которых мы привыкли ее воплощать, но лишь «исходит из некоторых терминов... и из некоторых основных предложений, из которых она разматывается … путем последовательного замещения терминов, совершенно независимо от того содержания, которое в эти термины вкладывается» [18]. Система образов является не более чем интерпретацией геометрии. Поэтому для успешного понимания современной геометрии студентам необходимо прививать умение решать задачи абстрактно-логическим выводом, а не наглядным контролем.

Начертательная геометрия — первая дисциплина, в которой студентам приходится управлять некоторым объектом (фигурами трехмерного пространства), используя в качестве интерфейса управления связи вторичных объектов (проекций) с объектом управления, когда каждый вторичный объект отражает лишь отдельные параметры объекта управления. В дальнейшем такая задача возникает перед ними всякий раз, когда речь идет о многопараметрических системах и процессах (например, в атомной, тепло- и электроэнергетике).

Недостатки (1) — (2), являющиеся результатом снижения качества школьного образования, становятся причиной того, что студенты при изучении курса начертательной геометрии испытывают сложности в проверке собственных решений. Фактически они оказываются неспособны осуществлять этапы доказательства и исследования. Повысить уровень овладения материалом в условиях слабой подготовленности можно лишь методом многочисленных проб и ошибок, доведения до автоматизма простейших приемов и приобретения положительного опыта самостоятельного решения.

В частности, хорошие результаты показывает такой порядок обучения: студент знакомится с алгоритмом, закрепляет его применение решением типовых задач, после чего становится способен осмыслить содержание алгоритма, значение отдельных действий и т. д. К сожалению, это повышает нагрузку на преподавателя, вынужденного проверять все решения. Как отмечалось выше, эту функцию должна взять на себя компьютерная система. Выделим три группы задач верификации с примерами инженерно-графических задач:

1) верификация упражнений (проверка элементарных навыков): построение двух- и трехкартинного чертежа точки, прямой; построение проекций прямых и плоскостей частного положения, построение проекций точек в методах преобразования чертежа, применение правила прямоугольного треугольника и т. д.

2) верификация задач (проверка умения применять алгоритмы и находить результат): многошаговые метрические, позиционные и комплексные задачи.

3) верификация оформления решений.

Компьютерные технологии верификации

Рассмотрим примеры компьютерных технологий, обеспечивающих верифицируемость при изучении некоторых дисциплин:

1. Верифицируемость в программировании.

Изучая программирование, студенты пишут программы на каком-либо языке. Проверка программ выполняется на двух уровнях: на уровне синтаксиса (форма) и на уровне исполнения (содержание). Использование компиляторов обеспечивает верификацию на уровне синтаксиса (3-я группа): программа не будет передана на исполнение, если текст содержит какие-либо ошибки.

Хотя проверка (тестирование и автотестирование) кода является серьезной проблемой области разработки программного обеспечения [19], на этапе изучения основ программирования возможность запустить программу достаточна для самопроверки . Если результаты работы программы неудовлетворительны, вносятся исправления и следует новый запуск. Программу можно изменять и проверять до окончательного решения задачи (2-я группа). В настоящее время этот простой и достаточно эффективный метод дополняют технологии автоматического обучения, когда перед обучаемым ставят частные задачи — исправить фрагмент кода, вставить несколько строк и т. п. под контролем компьютерной системы (1-я группа), пример такой системы — [20].

2. Верифицируемость в высшей математике.

Многие задачи, с которыми встречается студент при изучении курса высшей математики также верифицируемы. Компьютерные системы типа MathCAD позволяют проверить любые вычисления (решение уравнений и систем, построение графиков, расчет определителей и матричные операции и др.), некоторые задачи преобразования выражений (упрощение, раскрытие скобок, дифференцирование, интегрирование). Еще больше возможностей предоставляют профессиональные пакеты символьной математики (Mapple, Mathematica). Наконец, в интернете имеется множество онлайн-калькуляторов для проверки частных задач (примеры — на сайтах http://ru.onlinemschool.com/math/assistance/, http://planetcalc.ru/search/?tag=178 и др.).

Верифицируемость в инженерно-графических дисциплинах

Верифицируемость в инженерно-графических дисциплинах в настоящее время обеспечивается применением CAD-систем:

Во-первых, это задачи, связанные с моделированием трехмерных фигур (1-я и 2-я группа): построение сечений, проекций линий пересечения, создание деталей и сборок.

Выше было показано, какие проблемы испытывает современный студент при проекционном моделировании. Трехмерные CAD-системы дают возможность их обойти: для проверки становится не нужным анализировать проекционные свойства фигур, достаточно рассмотреть моделируемый предмет со всех сторон. Вероятно, в этом одна из причин привлекательности трехмерных CAD-систем для студентов, которая была воспринята многими преподавателями как преимущество 3D-технологий перед традиционными методами начертательной геометрии.

Отметим, что, несмотря на все достоинства CAD-систем, такой подход почти полностью упускает приобретение опыта работы с формальными моделями, о важности которого упоминалось выше.

Во-вторых, верифицируемость многих задач начертательной геометрии обеспечивается высокой точностью построений в CAD-редакторах (1-я и 2-я группа). Так, в сборнике задач [21] в конце решения предлагается произвести измерение на чертеже и сравнить с ответом. При ручном исполнении современный студент рискует никогда не добиться правильного ответа, но при использовании графического редактора такой способ самопроверки становится возможным.

В-третьих, некоторые возможности предоставляют системы нормоконтроля [22] (3- группа).

Тем не менее многие вопросы верификации инженерно-графических задач остаются не решенными.

2-я и 3-я группа задач верификации связаны с разработкой специальных геометрических редакторов и применением CAD-систем и требуют отдельного обстоятельного рассмотрения. Отметим только сходство проверки решений и оформления инженерно-графических задач с упомянутой выше проверкой программ: систему проверки можно представить себе как транслятор языка графического моделирования (проекционного чертежа), выполняющий синтаксическую проверку (проверку оформления) и предоставляющий результат моделирования в форме, пригодной для самопроверки (например, в виде трехмерной модели). Такого рода трансляция является частью задачи автоматического чтения чертежа. В настоящее время такие системы позволяют работать не только с точками и прямыми, но и с многогранниками, и телами вращения [23, 24].

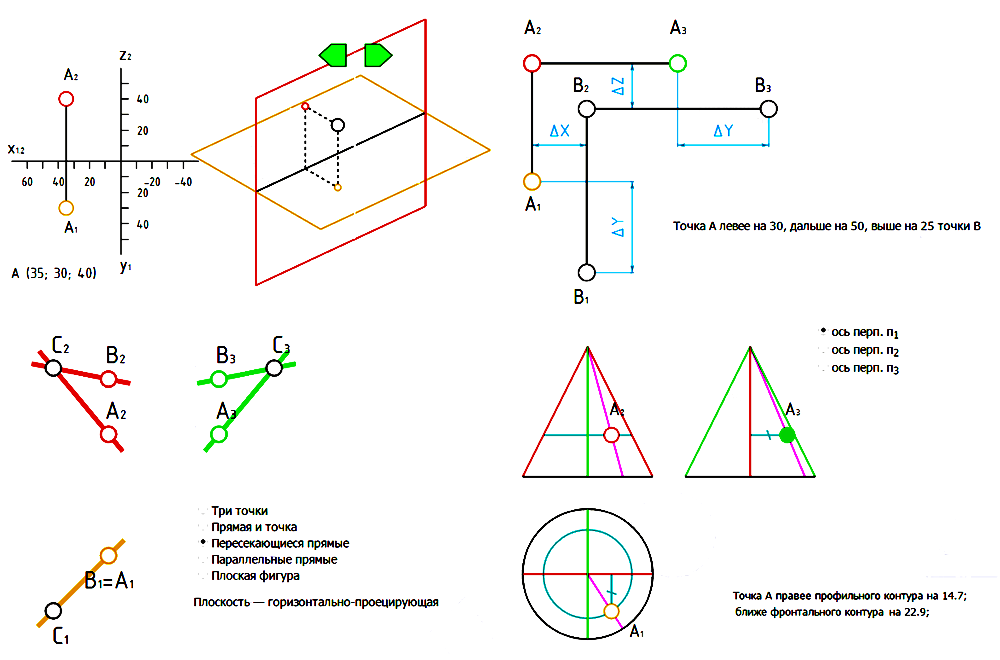
1-я группа задач верификации может быть решена при помощи геометро-графических тренажеров [25, 26]. Автором был разработан ряд интерактивных тренажеров для отработки элементарных приемов проекционного моделирования (рис. 1).

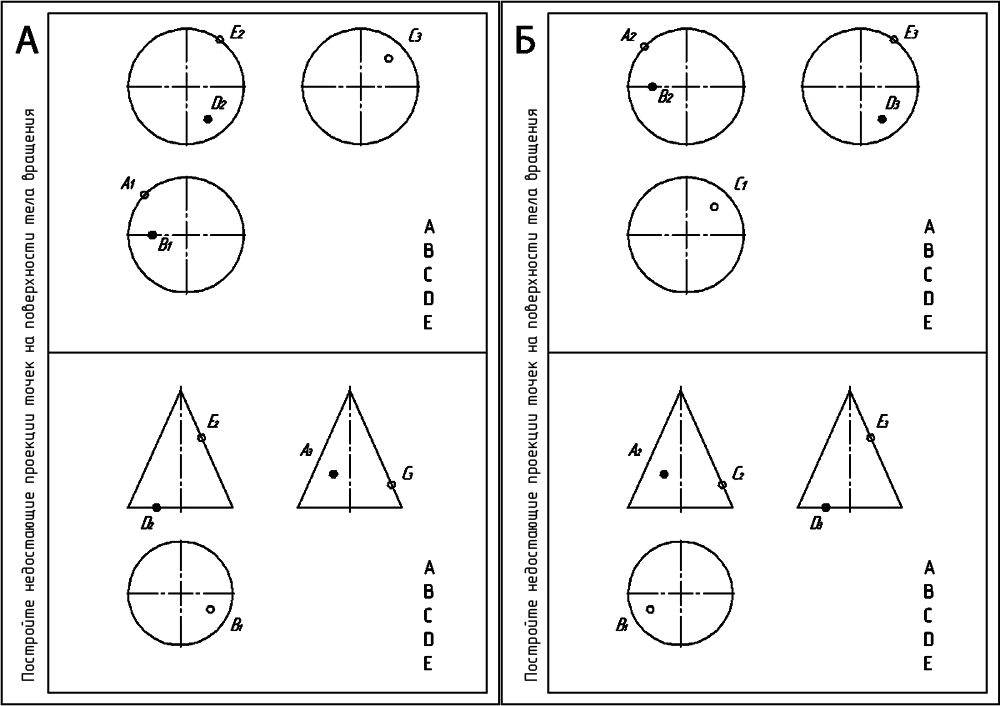
Тренажеры были опробованы на группе отстающих студентов в следующем режиме: студент получал карту заданий (вариант А или Б через одного), например, на построение проекций точек на поверхности вращения (рис. 2), выполнял построения, затем допускался к компьютеру и выполнял самопроверку, затем проверку выполнял преподаватель.

Результаты приведены в таблице 1: при первом использовании студенты нашли, в среднем (при расчете исключались минимальные значения и значения от 100% и выше), 63,4% ошибок. Разброс значений объясняется индивидуальными показателями усвоения той или иной темы и, в некоторой степени, сложностью интерфейса тренажеров.

Велико число однотипных ошибок, например, в заданиях на построение двухкартинного чертежа точек студенты применяли индексы 1-2 в системе плоскостей П₂-П₃, что автоматически аннулировало правильность расположения проекций. Причем, в ходе самопроверки студенты, ориентируясь на расположение проекций, оценивали свое решение как «правильное».

Использование тренажеров в режиме самопроверки показало следующее:

- при особенно низком уровне понимания тренажеры неэффективны: студенты произвольным образом интерпретируют то, что видят: не разделяют видимые и невидимые проекции точек, индексы проекций, не замечают параллелей на поверхностях вращения, сравнивают лишь примерное расположение;

- тренажеры интересны студентам и мотивируют их к исследованию моделей, так, некоторые студенты, потратив по собственной инициативе 15-25 минут на работу с тренажером, попросили дополнительное задание (давался другой вариант — Б или А, соответственно). Результаты приведены в таблице 2;

- применение нескольких тренажеров подряд приводит к путанице, так, проверяя задачи на построение двухкартинных чертежей сначала в тренажере с системой плоскостей П₁-П₂, а затем — П₂-П₃, при повторном решении студенты допустили больше ошибок при построении проекций в системе П₂-П₃ — располагали проекции одну под другой (столбцы 3 и 4, табл. 2).

- были обнаружены недостатки интерфейсов тренажеров, в частности, невозможность мгновенно поменять видимость проекции точки на поверхности (перемена знака соответствующей координаты) вызывала ошибки интерпретации результата сверки (случаи, когда студенты нашли больше ошибок, чем допустили, — столбцы Б.1 и Б.3, табл. 1).

Некоторые вопросы еще требуют решения: так, не найдена пока приемлемая форма представления заданий с плоскостями общего положения и многогранниками (различные варианты исходных данных приводят к усложнению интерфейса тренажера), хотя такая проверка легко автоматизируется средствами системы проверки решений (2-я группа задач верификации) [27].

В целом, эффект использования тренажеров можно оценивать как положительный. Незначительная модификация тренажеров делает их пригодными для автоматического контроля при выполнении заданий типа: разместить проекции точки, заданной координатами или положением относительно другой точки, расположить проекции прямой или плоскости заданного частного положения, поместить точку на заданный контур поверхности, выбрать положение секущей плоскости и др.

Таблица 1. Результаты применения тренажеров в режиме самопроверки

Таблица 2. Результаты повторной проверки после работы с тренажером

Выводы

Показано, что основу самостоятельной проверки решений инженерно-графических задач составляет понимание свойств проекций и умение логическим выводом проверять выполнение условий задачи; проверку обеспечивает этап доказательства в решении задачи.

Выявлено, что современные студенты испытывают трудности при выполнении самостоятельной проверки традиционным способом, требуются новые формы организации проверки, а основные компьютерные технологии преподавания инженерно-графических дисциплин не обеспечивают контроль знаний выше уровня «знакомство».

Выделены группы задач верификации.

Показано, что компьютерные технологии способны обеспечивать верифицируемость методов и алгоритмов в преподавании ряда дисциплин, но многие вопросы верификации в инженерно-графическом образовании остаются не решенными.

Показано применение геометро-графических тренажеров в задачах верификации элементарных приемов проекционного моделирования.

Список литературы

1. Bertoline G.R., Wiebe E.N. Engineering Graphics. Technical Craphics Communication. The 5th edition. The McGraw−Hill Companies, Inc. 2007. 820 p.

2. Государственная программа РФ «Развитие образования» на 2013–2020 гг. Министерство образования и науки РФ. URL: http://минобрнауки.рф/документы/3409/файл/2228/13.05.05-Госпрограмма-Развитие_образования_2013-2020.pdf (дата обращения: 09.03.2016)

3. Красильникова В. А. Концепция компьютерной технологии обучения. Оренбург: ОГУ, 2008. 42 с.

4. Пидкасистый П. И. Самостоятельная познавательная деятельность школьников в обучении. М.: Педагогика, 1980. 240 с.

5. Латыпова В.А. Методики проверки работ со сложным результатом в условиях смешанного и дистанционного автоматизированного обучения // Интернет-журнал «Науковедение» Том 7, №3 (2015). URL: http://naukovedenie.ru/PDF/170TVN315.pdf DOI: 10.15862/170TVN315 (Дата обращения: 17.01.2016)

6. Аргунов Б.И., Балк М.Б. Геометрические построения на плоскости: учебное пособие. М.: ГУПИ Министерства Просвещения РСФСР, 1957. 268 с.

7. Глоговский В.В. Элементарные конструктивные задачи по начертательной геометрии. Львов: Вища школа, 1981. 152 с.

8. Столер В. А. Преподавание начертательной геометрии с использованием компьютерно-мультимедийных систем // II Международная интернет-конференция «Проблемы качества графической подготовки студентов в техническом вузе в условиях ФГОС ВПО» КГП-2011 (февраль-март 2011 года). URL: http://dgng.pstu.ru/conf2011/papers/7/ (дата обращения: 16.01.2016)

9. Мельник О. П. Методы и особенности составления тестовых заданий для дистанционных курсов геометро-графических дисциплин / О. П. Мельник, Я. Г. Скорюкова, Е. В. Слободянюк // Проблемы качества графической подготовки студентов в техническом вузе: традиции и инновации. Материалы V Междунар. научно-практ. интернет-конференции (г. Пермь, февраль — март 2015 г.). Пермь: Изд-во ПНИПУ, 2015. С. 279-289.

10. Столбова И. Д. О создании учебно-методического комплекса для сопровождения графической подготовки студентов / И. Д. Столбова [и др.]. // Геометрия и графика. М.: ИНФРА-М, 2015. Т. 3. Вып. 2. С. 29-37.

11. Полушина Т. А. Интернет-тренажер по начертательной геометрии и инженерной графике в учебном процессе // Геометрия и графика. М.: ИНФРА-М, 2013. Т. 1. Вып. 2. С. 31-37.

12. Болбат О. Б. Использование мультимедийных презентаций в учебном процессе // Проблемы качества графической подготовки студентов в техническом вузе: традиции и инновации. Материалы V Междунар. научно-практ. интернет-конференции (г. Пермь, февраль — март 2015 г.). Пермь: Изд-во ПНИПУ, 2015. С. 224-229.

13. Сергеева И. А., Петухова А. В. Инженерно-графическая подготовка студентов в условиях компьютеризации обучения // Интернет-журнал Науковедение. 2014. №3 (22). URL: http://naukovedenie.ru/PDF/107PVN314.pdf (Дата обращения: 16.01.2016)

14. Ботвинников А. Д. Современные технические средства обучения черчению // Новые технические средства обучения черчению. М.: Просвещение, 1967. С. 3-17

15. Беспалько В. П. Каковы же наши принципиальные возможности? // Вестник высшей школы. 1965, №6.

16. Талалай П. Г. Начертательная геометрия. Инженерная графика. Интернет-тестирование базовых знаний. СПб.: Лань, 2010. 288 с.

17. Фролов С. А. Сборник задач по начертательной геометрии. М.: Машиностроение, 1986. 176 с.

18. Каган В. Ф. Задача обоснования геометрии в современной постановке // Очерки по геометрии. М.: Изд-во Московского ун-та, 1963. С. 27-56.

19. Майерс Г. Искусство тестирования программ. М.: Финансы и статистика, 1982.

20. HTML Academy: интерактивные онлайн-курсы. URL: http://htmlacademy.ru (Дата обращения: 9.03.2016)

21. Задачник по начертательной геометрии с элементами программирования. Воронеж: Изд-во ВГУ, 1984. 176 с.

22. Петухова А. В. Использование утилиты «Нормоконтроль» для автоматизации проверки чертежей // Материалы II Международной научно-практической конференции «Проблемы качества графической подготовки студентов в техническом вузе в условиях ФГОС ВПО». Пермь: Изд-во ПГТУ, 2011. С. 197-199.

23. Ротков С.И. Разработка методов и средств геометрического моделирования и компьютерной графики пространственных объектов для CALS-технологий. Дис. ... докт. техн. наук: 05.01.01. Нижний Новгород, ННГАСУ, 1999. 280 с.

24. Тюрина В.А. Разработка методов преобразования каркасной модели в задаче синтеза образа 3D объекта по его проекциям. Дис. ... канд. техн. наук: 05.01.01. Нижний Новгород, ННГАСУ, 2003. 170 с.

25. Бойков А. А. Геометрическое моделирование в системе дистанционного обучения / Геометрия и графика. М.: Инфра-М. 2014. Том 2. Выпуск 4. С. 34-42. DOI: 10.12737/8295

26. Бойков А. А. О применении графических мультитестов в системе компьютерного обучения по инженерной графике // Проблемы качества графической подготовки студентов в техническом вузе: традиции и инновации. Материалы V Междунар. научно-практ. интернет-конференции (г. Пермь, февраль — март 2015 г.). Пермь: Изд-во ПНИПУ, 2015. С. 341-355

27. Бойков А. А., Милосердов Е. П., Федотов А. М. Средства компьютерного обучения графическим дисциплинам // Проблемы научно-методического и организационного обеспечения учебного процесса по начертательной геометрии, инженерной и компьютерной графике: сборник трудов Всерос. семинара-совещания заведующих кафедрами графических дисциплин. Саратов: СГТУ. 2005. С.27-29.

Рисунки к докладу

Примеры геометро-графических тренажеров для самопроверки

Пример карты с заданием (варианты А и Б)

Тихонов-Бугров Дмитрий Евгеньевич (14 марта 2016 г. 16:16)	Уважаемый Алексей Александрович, Вы блестяще охрактеризовали основную массу продукта ЕГЭ: не могут; не умеют; не тренируют; избегают умственной обработки информации. Отличный анализ, интересные разработки. Может быть это выход из положения для коллег, имеющих один семестр и 58 часов. Мне известен вуз, где в подобной ситуации студенты сидят часами за подобным тренажёрами и почти никакого учебного процесса.  Теперь о "печально показательном учебнике" П.Г.Талалая. Павел Григорьевич пожалуй первым в стране попал под "борьбу за объективность оценки знаний". Руководство вуза заставило его превратить экзамен по НГ в копилку тестов. Ему говорили: сделай как в Норвегии: уборщица выдаёт задание, студенты за отведённое время отмечают ответы, она собирает и относит на ВЦ для обработки. Никаких преподов. Мы много раз обсуждали ситуацию, старались смягчить. И тут настало время Интернет-тестирования остаточных знаний, необходимого для аттестации вуза. Талалай лучше всех на тот период разбирался в этой кухне. По  этой причине издательство Лань с моей подчи обратилось к д.т.н. проф. Талалаю написать НЕ УЧЕБНИК, а книжку о том, как успешно отвязаться от такого тестирования. Книжка имела большой успех. Издательство выпустило целую серию таких книг по разным предметам. Замечательно, что Интернет-тестирование почило в бозе. А книга свою важную роль сыграла.
Бойков Алексей Александрович (15 марта 2016 г. 22:37)	Уважаемый Дмитрий Евгеньевич, спасибо за высокую оценку! Ваше мнение очень важно для меня, мне памятен пример с шахматами, приведенный Вами в докладе КГП-2011. Ваш доклад и еще Дениса Вячеславовича о "будущем начертательной геометрии" тогда заставил меня иначе взглянуть на происходящее в геометро-графическом образовании. По поводу пособия Павла Григорьевича пусть это будет репликой о книге, как "артефакте". Она передо мной возникла при следующих обстоятельствах. Вместо февральских каникул мы едва ли не всей кафедрой посещали курсы повышения квалификации, на которых нас обрадовали, что программы в этом году придется переделывать дважды (весной и в сентябре). И там же рекомендовали включить в список литературы учебники "Лани", доступные в читальных залах института в электронном виде. В поиске по "начертательной геометрии" и по "инженерной графике" эта книжка - первая или одна из первых. Отношение к интернет-тестированию у меня резкое - вопросы многие поставлены из рук вон плохо, чертежи - ужасные, студенты, используя режим самоподготовки, легко "натаскивают" себя на 3 и 4, а потом благополучно заваливают зачет. И неизвестно, что с ними делать после этого.
Хейфец Александр Львович (16 марта 2016 г. 8:43)	Алексей Александрович, здравствуйте. По Вашему докладу: 1. О терминологии. Я правильно понял, что студент решает задачу на компьютере, указывает свой  ответ, а компьютер его проверяет? Если так, то  это не самоконтроль студента, а контроль со стороны компьютера, котому преподаватель передал алгоритм проверки. 2. Кто делает карты контроля - преподаватель? Если так, то студенты быстро перефотографируют карты, передадут их друг другу и вся система контоля - дискредитирована.   3. Огорчает Ваше отношение к 3d. Развивать формальное мышление следует на современных примерах и 3d задачах, а не оглядыдваться назад к проекционным методам. В этом плане Вашу работу воспринимаю как "из пушки по воробьям". Вы владеете современными компьютерными технологиями, а применяете их для работ вчерашнего дня. Видимо, здесь что-то лично-диссертационное (кстати, как дела на этом фронте?). 4. Досадно, что Вам не знакомы мои работы того же направления. Зайдите на закладку Участникии найдите мой доклад на нашей 1-ой КГП. Там рассмотрен автоматизированный коллоквиум, в котором задачи случайным образом генерирует компьютер, студент выполняет решение, компьютер его проверяет и задает дополнительные вопросы. Затем компьютер, по специальному "педагогическому алгоритму" ставит оценку.  Поскольку заложен генератор случайных параметров, то коллоквиум является и тренажером. Реши 100 задач с различными параметрами, реши их дома, а потом приди и реши ее 101-ый раз как колоквиум.  Это направление я развиваю, активно применяю автоматизированный контроль по темам и для проведения олимпиад. На олимпиаде побеждает тот, кто решит больше задач и наберет больше баллов. С уважением. А.Л. Хейфец
Бойков Алексей Александрович (16 марта 2016 г. 12:04)	Уважаемый Александр Львович, здравствуйте. Рад снова общаться. Спасибо за внимание к моему докладу и замечания. 1. Что касается терминологии, если мы предполагаем у студента желание научиться, как того подразумевают все образовательные инновации, то любая автоматизированная проверка на стратегическом уровне является самопроверкой. В этом смысле я обобщаю. Предположим, школьник учится умножать в столбик и сверяет свой ответ с решением компьютера - что это?  2. Конкретно в данной работе контроль имел статистические задачи. Карты контроля составлялись преподавателем. Тренажер служит для самоподготовки. Экзамен они все равно сдают преподавателю лично, а на контрольных работах решают задачи. 3. Мое отношение к 3d сугубо положительное - к 3d, 4d, ... Чертеж, я считаю, более удобным инструментом для отработки навыков формальных методов моделирования, а достоинства 3d пакетов проявляются лишь в прикладной области предметного моделирования и автоматизации подготовки конструкторской документации. При использовании AutoCAD'а, если мы захотим чего-то большего, чем стандартные инструменты, мы будем вынуждены браться за LISP. Что далеко выходит за рамки отведенных часов и задач. 4. Спасибо за ссылку на Ваш доклад. В моих основных исследованиях (автоматизация проверки решений задач), я также пришел к автогенерации исходных заданий, но, пока не решена проблема автоматической расстановки обозначений, эта технология применяется мной ограниченно. с уважением, Бойков
Тихонов-Бугров Дмитрий Евгеньевич (16 марта 2016 г. 18:11)	Уважаемый Алексей Александрович, Вашу мысль под №3 я повешу на стенке своего кабинета, чтобы посетители не задавали лишних вопросов. Спасибо. 3. Мое отношение к 3d сугубо положительное - к 3d, 4d, ... Чертеж, я считаю, более удобным инструментом для отработки навыков формальных методов моделирования, а достоинства 3d пакетов проявляются лишь в прикладной области предметного моделирования и автоматизации подготовки конструкторской документации. При использовании AutoCAD'а, если мы захотим чего-то большего, чем стандартные инструменты, мы будем вынуждены браться за LISP. Что далеко выходит за рамки отведенных часов и задач.
Хейфец Александр Львович (16 марта 2016 г. 21:27)	Алексей Александрович, или А по сути я еще раз утверждаю, что учить нужно тому, что востребовано в прикладных задачах и не откладывать и не перекладывать это на потом. Сокращать НГ и учить теории 3D. А если нужно учить Lisp'у - значит и ему, родному. Хотя, понимаю, что сейчас при нынешнем контигенте преподавателей это нереально. Но со временем...  Кстати Вам знакома моя толстая книга  (Москва, 2002 г., 400 с.) по программированию графической информации на AutoLisp'е. Я и сейчас ему учу. С уважением. А.Л. Хейфец
Сальков Николай Андреевич (17 марта 2016 г. 0:44)	Здравствуйте, Алексей Александрович! Замечательная статья! В свою очередь, я, как и Дмитрий Евгеньевич, состряпаю плакаты и повешу не только в институте, но и дома! И Вышнепольскому посоветую! "Мое отношение к 3d сугубо положительное - к 3d, 4d, ... Чертеж, я считаю, более удобным инструментом для отработки навыков формальных методов моделирования, а достоинства 3d пакетов проявляются лишь в прикладной области предметного моделирования и автоматизации подготовки конструкторской документации. При использовании AutoCAD'а, если мы захотим чего-то большего, чем стандартные инструменты, мы будем вынуждены браться за LISP. Что далеко выходит за рамки отведенных часов и задач." Если даются для  всего курса только 8 лекций и 8 практических и если сюда потребуется воткнуть еще и информационные технологии, то все выделенные часы будут потрачены исключительно для обучения студентов информационным технологиям, и ни секунды - основам конструирования!  Нельзя табурет "сварганить" за 10 секунд!
Бойков Алексей Александрович (17 марта 2016 г. 17:20)	Уважаемые Дмитрий Евгеньевич и Николай Андреевич, спасибо! Я очень рад, что наши мнения в этом вопросе совпадают.
Бойков Алексей Александрович (17 марта 2016 г. 17:40)	Уважаемый Александр Львович, я полностью согласен с Вами в том, что трехмерная геометрия - это очень хорошо, и что решать задачи трехмерного моделирования с использованием 3D-пакетов полезно и нужно. Вашу книгу 2002 года я неоднократно давал ребятам с факультета информатики для углубления знаний Автокада, в том числе для знакомства с AutoLISP'ом. Тем не менее, я не считаю, что изучать Lisp (тем более, диалект AutoLISP) - первоочередная задача геометрического образования. Программировать геометрические задачи можно в Python (Компас) или сразу в C++ (он тоже стыкуется с некоторыми пакетами), неважно. Я вижу цель геометрического образования в изучении геометрии, и чем меньше будет посредников, тем лучше. Я позволю себе продолжить Вашу аналогию. Если "развивать формальное мышление следует на современных примерах и 3d задачах" в системе AutoCAD, тогда всю высшую математику давно пора переводить на MathCAD, MathLab, а еще лучше сразу на Mapple или Mathematica, и перестать уже решать типовые расчеты - брать производные, интегралы, считать матрицы, преобразовывать выражения и выполнять прочие работы "вчерашнего дня". Современные специалисты должны решать современные задачи, и им вовсе не обязательно знать и задумываться, как работают их инструменты. С уважением, Бойков.
Головнин Алексей Алексеевич (17 марта 2016 г. 18:24)	Здравствуйте Алексей Александрович, здравствуйте Александр Львович! Вопрос наверное к Алексею Александровичу. Вы совсем не упомянули, что программирование в AutoCAD доступно для специалистов в Visual BASIC и VBA. VBA, к тому же, встроен в среду AutoCAD, и нет необходимости приобретать дополнителные программные средства.  http://www.itshop.ru/Programirovanie-v-AutoCAD-s-pomoshhyu-VBA/l9i30007 Я не программирую в Автокаде, но знакомился давно AutoLISPом, а недавно узнал, что он устарел. Если Вы в курсе и Вам это интересно и не сложно, то просветите пожалуйста в двух словах. С уважением Головнин А.А.
Хейфец Александр Львович (17 марта 2016 г. 23:08)	Алексей Алексеевич, по поводу, устрел ли AutoLisp. AutoLisp не устарел. Это происки конкурентов AutoLisp'а, не более. Особенно, применительно к нашей сфере деятельности - программному формированию графических объектов. Вышло и выходит много литературы по программированию на AutoLisp. (И я  внес свой вклад - книга по программированию "Инженерная компьютерная графика", М., 2002, 430 с., рекомендую, и в последней книге-учебнике "Инженерная 3d компьютерная графика", М., 2015, 602 с.тоже немало примеров по программированию на этом языке). Но я не встречал книг о программировании в AutoCAD'е на других встроенных в него языках VBA и Si++. Не встречал книг по программированию в Компасе, 3dSMAX, SW и других пакетах. Оно есть, но закрыто для простых пользователей и не "популяризируется".  Я преподаю кратко AutoLisp на выпускающей кафедре в спецкурсе компьютерной графики (подрабатываю). Все свои модели программирую, ибо сразу возможна многовариантность и оптимизация. Сделать что-то серьёзно-современное без программирования невозможно. Язык очень простой. Говорят, что "там" он преподается в колледжах. Интересен вопрос о соотношении программирования и параметризации. Параметризация - для тех, кто боится программирования или не хочет составить программу. Это отдельная интересная тема для обсуждения для тех, ко действительно занимается современным геометрическим моделированием. С уважением. А.Л. Хейфец
Бойков Алексей Александрович (17 марта 2016 г. 23:36)	Алексей Алексеевич, вряд ли я Вам серьезно помогу. Сам я имею опыт программирования AutoCAD только на AutoLISP. Мое недовольство этим диалектом связано не с автокадом, а с тем, что AutoLISP во многом противоречит идеологии функционального программирования Lisp вообще. Автокад поддерживает несколько технологий программирования - AutoLISP, VB, VBA, VB.NET, C++, C#. Некоторым из них периодически пророчат устарение и умирание, но, учитывая число пользователей по всему миру, думаю, до этого не дойдет. На сайте Autodesk (2012 год) про это ни слова http://www.autodesk.ru/adsk/servlet/item?siteID=871736&id=18221924 . С уважением, Бойков.
Волошинов Денис Вячеславович (18 марта 2016 г. 22:09)	Алексей Александрович, хотел бы обратить Ваше внимание на автогенерацию в Симплексе программы на языке Prolog, эквивалентной тому построению, которое формируется в результате синтеза алгорима посредством чертежа. В Симплекс встроен интерпретатор языка Prolog, и он взаимодействует с геометрической базой как в смысле анализа, так и в смысле синтеза алгоритмов, которые сразу же могут быть исполнены и отображены. Мощь логического программирования, объединенного с конструктивным геометрическим моделированием, может дать весьма интересные результаты в деле автоматизации проверки решений геометрических задач. И не только. Автоматический синтез геометрических алгоритмов, заданных правилами Prolog, - это возможность забираться в такие "геометрические дебри", к которым без подобных информационных средств даже помыслить невозможно. Prolog в Симплексе требует еще большого внимания с точки зрения обеспечения его эффективного функционирования, но даже сейчас задача сравнения алгоритма с эталоном-образцом, выраженным через геометрическое построение в логических переменных, - вполне реальное дело. Алексей Александрович, если Вас подобный подход заинтересует, то буду рад поделиться с Вами своими мыслями и наработками. С уважением, Д.Волошинов
Бойков Алексей Александрович (22 марта 2016 г. 22:58)	Уважаемый Денис Вячеславович, буду признателен за любую информацию. Несколько лет назад я дошел до необходимости использовать что-то вроде геометрического Пролога для автоматизации проверки, но из-за отсутствия подходящих редакторов был вынужден заняться их разработкой. С уважением, Бойков.