

|
Ракитская Мария Валентиновна | (Балтийский государственный технический университет «ВОЕНМЕХ» им. Д.Ф. Устинова) |
В статье рассматриваются проблемы развития рефлексии у студентов младших курсов технических вузов. В качестве одного из средств решения проблемы предлагается использовать ТРИЗ при обучении начертательной геометрии.
Критики отечественного образования, особенно школьного, отмечают в качестве главного недостатка слабое развитие рефлексии учащихся. Термин рефлексия имеет большое количество трактовок. Отметим две традиции в трактовке рефлексивных процессов:
Рефлексия обеспечивает индивидууму выход из полной поглощённости непосредственным процессом жизни для выработки соответствующего отношения к ней, вне её, для суждения о ней [1]. Г.П.Щедровицкий отмечает [2],что новые средства и способы деятельности могут появиться у человека, если сама деятельность становится предметом специальной обработки, чтобы на неё направилась бы новая, вторичная деятельность. При этом, вторичная деятельность как бы поглощает исходную как материал.
В учебной деятельности авторефлексия и самооценка существенно сближаются. Можно выделить два уровня рефлексии [3]: формальную (самооценка) и содержательную, которая направлена на то, чтобы обнаружить, почему данное действие выполняется так, а не иначе, что является причиной успешного выполнения в различных условиях.
Для проведения рефлексивного анализа, от обучающегося требуется целый комплекс умений:
Если школьник привык действовать по указке и шаблону, то в условиях свободы, попадания в нестандартную ситуацию, он теряется. Он не готов к творчеству, разнообразным формам мышления, к сотрудничеству. Хорошо, если хотя бы бытовые проблемы в какой-то мере способствуют нахождению выхода из положения в нестандартной ситуации (не поворачивается ключ в замке, не работает купленная игрушка, не разобрать газонокосилкуи т. п.).
К сожалению, развитию инновационного обучения в значительной степени препятствует ЕГЭ, который является лишь оценкой знания школьниками содержания предметов. Подобного рода тесты не являются инструментом оценки уровня компетенций [4], и не характеризуют степень готовности к обучению в вузе. Общеизвестно, что по результатам ЕГЭ оценивается успешность работы учителя и школы. Отсюда понятно, на что направлена учебная работа, и тут не до инноваций.
Всевозможные входные тесты, проводимые вузами показывают, что большинство абитуриентов не обладает достаточной базовой подготовкой (особенно по геометрии и графике) и способностью к устойчивой рефлексии.
Ликвидацией указанных недостатков вынуждены заниматься, в первую очередь, кафедры, преподающие графические дисциплины. При обучении начертательной геометрии нужно использовать разные средства и способы развития рефлексии. Весьма важно, если эти средства послужат базой для дальнейшего развития ключевых профессиональных компетенций. Одним из таких средств следует признать ТРИЗ.
ТРИЗ – теория решения изобретательских задач – область знаний, исследующая механизмы развития технических систем с целью создания практических методов решения изобретательских задач, разработанная Альтшуллером Г.С [5] . Уровень знаний не позволяет первокурсникам заниматься изобретательством в полном смысле этого слова, но алгоритмы, которые используются в ТРИЗ, могут быть использованы для развития мышления студента. АРИЗ (алгоритм решения изобретательских задач), прежде всего, является инструментом для решения конкретных технических задач. А такой инструмент, если его долго и регулярно применять, оказывает влияние на человека, использующего этот инструмент, и развивает его мышление.
В задачах начертательной геометрии с помощью перебора различных подходов и выбора из них оптимального студент учится анализу, выбору наилучшего решения.
В АРИЗ часто пользуются методом зеленых человечков, т.е. представляют какой-либо объект, состоящих из нескольких мелких частей. В начертательной геометрии для этого метода тоже существует широкая возможность применения, например, построение теней от объектов: какая-то часть человечков приземляется на поверхность и не попадает на расположенную за ней поверхность или плоскость, остальные человечки на нее попадают.
Необходим анализ конфликта в модели задачи. Например, при построении условной развертки поверхности вращения необходимо провести аппроксимацию окружности. Два противоречия: если окружность разделить на небольшое число частей (6 или 8), то замена хордой дуги окружности будет давать большую ошибку, если этих частей будет слишком много, то возникает ошибка при откладывании. Надо выбрать оптимум.
Полезно научить студента разделять какую-то сложную поверхность на несколько частей. К примеру, проектируем какую-ту необычную крышу, которая представляет собой поверхность с двумя направляющими и плоскостью параллелизма (поверхность Каталана). Надо выбрать каркас, а также посчитать площадь (приблизительно). Удобно сделать аппроксимацию треугольниками, а потом построить условную развертку.
Важно, когда студент учится объединять условия задачи. Задача. В выемку, имеющую форму трехгранного угла с вершиной S и глубиной h, помещен шар диаметром 0.5h. Найти положение центра шара.
В этой задаче надо понять, что раз имеет место касание, то (свойство касательной плоскости) можно построить нормаль, через точку касания, а эта нормаль обязательно у шара проходит через центр. С другой стороны центр сферы всегда располагается на расстоянии радиуса от точки касания. Таким образом, строим 3 плоскости, удаленные на расстояние радиуса от каждой из плоскостей трехгранного угла, причем плоскости строим вовнутрь трехгранного угла, и объединяем условия (исключаем противоречия), т.е. находим геометрическое место точек их пересечений. Это и будет искомый центр сферы.
Альтшуллер рассматривал задачу, где в лаборатории в большой бак с жидкостью падали (случайно) различные предметы, и их из бака необходимо было доставать. При этом предметы были очень разные, и каждый раз приходилось решать новую задачу. Так и в начертательной геометрии (геометрической оптике) встречаются задачи, принцип решения которых основан на равенстве углов падения и отражения. Принцип один, но если рассматривать эту задачу при построении отражения от плоскости – одна последовательность действий, а при отражении от поверхности сферы, тора или конуса задача существенно меняется.
Очень полезно решать обратные задачи. Например, известное правило прямоугольного треугольника (определение истинной величины отрезка). Обычно задача решается «впрямую» по проекциям ищется истинная величина отрезка. Допустим какой-то проекции точки конца отрезка нет, но при этом известно какое-либо другое данное, например, истинная величина отрезка. Как решать задачу в этом случае?
Одним словом, изучаем принцип решения задачи, а затем несколько изменяем условие. Изучаем, какие принципы решения неприемлемы, а что можно использовать. Устраняем противоречие и решаем задачу.
Представляют интерес задачи, когда необходимо соединить точки на поверхности кратчайшим путем. Разнообразие решения определяется объектом. Допустим, необходима прокладка кабеля по поверхности, состоящей из полуцилиндра и плоскости. Для решения этой задачи, скорее всего, необходимо построение развертки, а если поверхность - сфера – уже необходимо задавать плоскость, проходящую через центр сферы.
Очень помогает решение задач, которые имеют некоторый прикладной характер. Процесс решения даже учебных задач далеко не всегда бывает простым. Учащийся попадает в новую для себя ситуацию, из которой необходимо находить выход. Выдающийся математик и педагог Джордж Пойа [6] отмечал, что успешному решению сопутствует понимание особенностей процесса решения и технологии этого процесса, однако никакое описание или его теория не могут исчерпать многообразия его сторон, любое его описание или теория обязательно являются неполными, схематическими чрезвычайно упрощенными.
Помня о том, что не существует исчерпывающего описания творческого процесса, попытаемся составить приближенный план (алгоритм) решения прикладной конструктивной задачи.
Решение задачи необходимо начинать с преобразования ее условия к удобному виду, сведению задачи о реальных объектах к математической с помощью упрощения и абстракции. Анализируя исходные данные, мы осуществляем перевод условия задачи из прикладного (физического) русла в чисто математическое. У психологов этот процесс называется трансляцией. Назовем первый этап трансляцией постановки задачи. На этом этапе часто приходится решать, какими физическими условиями можно пренебречь. После этого можно думать о пространственной модели решения задачи. На этой стадии очень помогает анализ решения в двумерной постановке, выявлений особенностей перехода к трехмерной задаче. Обратимся снова к идеям Д.Пойа, которые помогут нам на этой и последующих стадиях решения. Существуют две категории мыслей: 1) те, которые мы порождаем активно, посредством акта мышления, обдумывания, 2) те, которые вспыхивают в нашем сознании самопроизвольно. К последним надо относиться как можно более внимательно, изучать насколько позволяют ваши способности. Такой анализ позволяет приобретать новые знания.
У студента появилась пространственная идея решения задачи? Включаем анализ: возможны ли другие? Если таковы имеются, то критерием выбора будет простота реализации решения на чертеже. Как свидетельствует Д.Пойа: не делайте при помощи большего то, что можно сделать при помощи меньшего.
Очередной этап - анализ способов построения (задания) на чертеже необходимых геометрических образов. На этом этапе мы вспоминаем необходимые сведения из теории, выбираем наиболее рациональные (удобные) способы - обеспечиваем соответствующие логические условия.
Теперь можно приступать к реализации решения на ортогональном чертеже. При этом не следует думать, что данный этап чисто технический. Учащемуся придется снова обеспечивать необходимые логические условия, выявлять и разрешать противоречия. Как отмечал Д.Пойа: никогда не идите наперекор своим ощущениям, но старайтесь также трезво взвесить все аргументы за и против ваших планов.
Задачи в начертательной геометрии можно отнести к творческим задачам. Для их решения студенту необходимо делать последовательно по направлению к результату два или более шага, несовместимых с его опытом действий в подобных ситуациях. Условия задачи, в том виде, в каком они попадают к студенту, называются исходной ситуацией. В ней содержится административное противоречие (АП), т.е. противоречие типа: «Надо получить то-то, но я не знаю, как это сделать». Любая исходная ситуация требует предварительной обработки - выделения из расплывчатой проблемы изобретательской задачи, которая должна содержать техническое противоречие.
Попробуем применить некоторые из приемов ТРИЗ при решении задач начертательной геометрии.
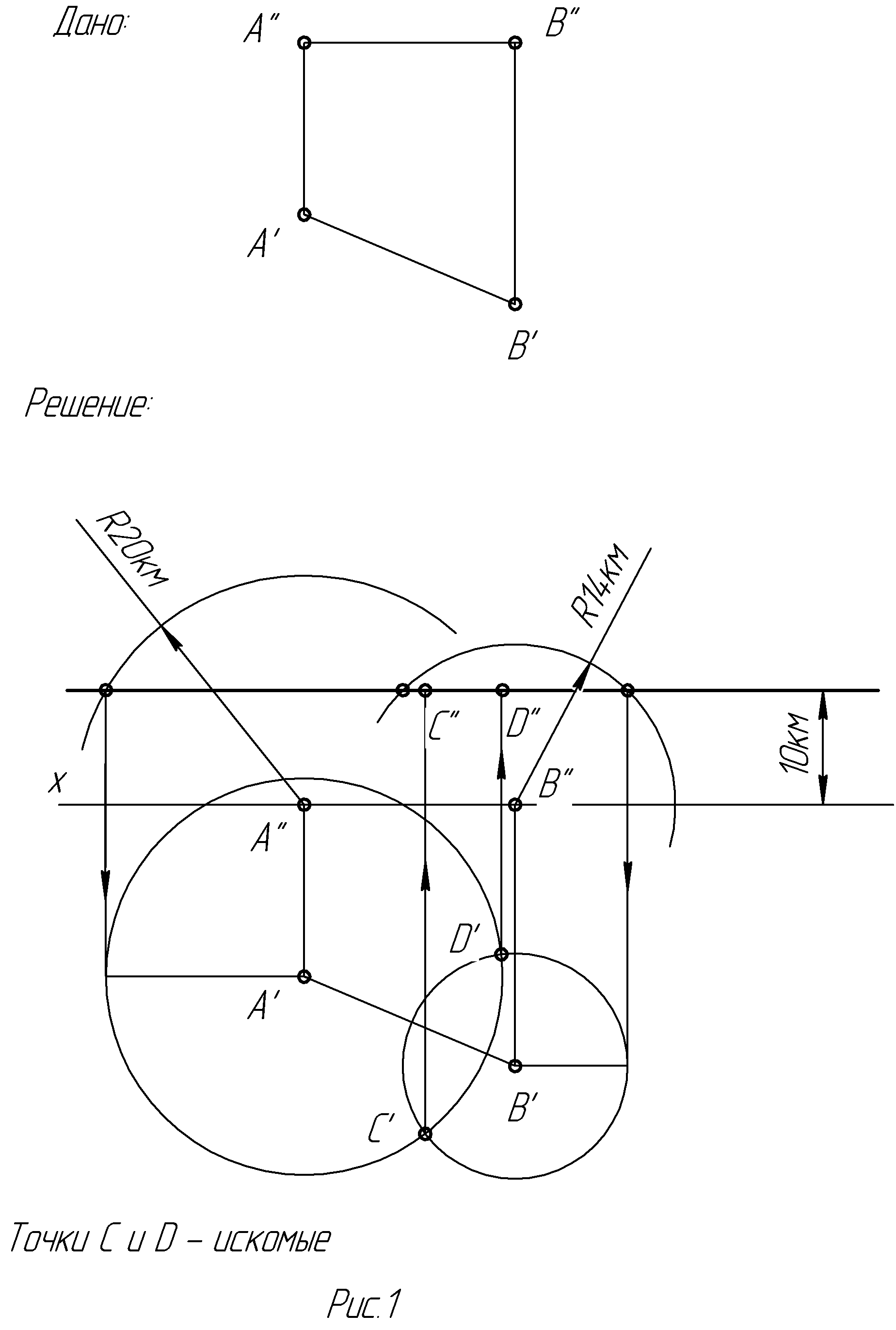
Задача 1. В точках А и В находятся лазеры (рис.1а). Определить точку взаимного положения ракеты, если ее расстояния до лазеров (наклонные дальности), равны соответственно 20 и 14 км. Высота полета 10км, АВ=20км.
Первое с чего начинается решение задачи - это с анализа ее условия. При этом вначале в голове возникает комплекс внешних и внутренних факторов, направляющий мысли по шаблонному пути, называемой психологической инерцией. Психологическая инерция мешает совершать необычные мыслительные операции, поэтому в ТРИЗ предусмотрены средства управления мышлением, защиты от ошибок. Различают три основных вида психологической инерции: инерция терминов, инерция образов, инерция узкой специальности.
Задача ставится в уже известных терминах. Каждый термин отражает старое, существующее техническое решение. И эти термины не остаются нейтральными, они навязывают изобретателю присущее им содержание. Изобретение же состоит в том, чтобы выйти за пределы известного, придать терминам новое содержание или полностью заменить их.
Один из самых простых и эффективных терминов гашения психологической инерции состоит в полном отказе от специальных терминов в ходе решения задачи. Надо использовать слова, не содержащие конкретного смысла, в том числе, из студенческого лексикона: «штуковина», «вещь», «объект».
Термины существуют для того, чтобы возможно надежнее, жестче оградить неизвестное от известного. Стоит убрать термины, как исчезают жесткие границы, и мысль намного свободнее отправляется в полёт в неизвестное.
Во многом успех решения задачи зависит от того, насколько сильно удастся расшатать, сломать систему исходных представлений. Чем глубже и подробнее человек знает предмет, тем крепче «сидит» в нем традиционный образ. Обширные знания о предмете, добытые иногда кропотливым трудом, заставляют человека активно защищаться от вторжения в его область.
При решении задачи 1 заменим лазеры материальными точками. Чтобы заменить ракету материальной точкой, оценим соотношение размеров ракеты (примерно D=1м, l=10м) и расстояний до лазеров (10,14,20 км). Так как (D,l<<a) размерами ракеты можно пренебречь и считать ракету материальной точкой. Движение материальной точки - плоская линия, так как высота полета сохраняется z=10км. (Вспомним уравнение плоскости). Нам задано расстояние от ракеты до лазеров. Геометрическое место точек равноудаленных от данной на плоскости - окружность, в пространстве - сфера. Перейдем теперь от физической формулировки задачи к математической:
Найти геометрическое место точек, принадлежащей плоскости z=10км и двум сферам, с центрами в точке А и В и радиусами 10 и 14 км. Проверим эквивалентность физической и математической задачи. Все ли условия мы учли?
Теперь решение можно разделить на два: ищем геометрическое место точек принадлежащих плоскости и сфере №1 и ищем геометрическое место точек, принадлежащее плоскости и сфере №2. Точка пересечения этих геометрических мест и есть искомая точка.
Главное в начале решения - уйти от прототипа, сбить психологическую инерцию. Для этого существует хороший прием: оператор РВС (размер, время, стоимость). Оператор РВС включает шесть мысленных экспериментов, перестраивающих условия задачи:
В физических задачах время и стоимость играют существенную роль. В начертательной геометрии оператор РВС можно применять в основном в отношении размеров.
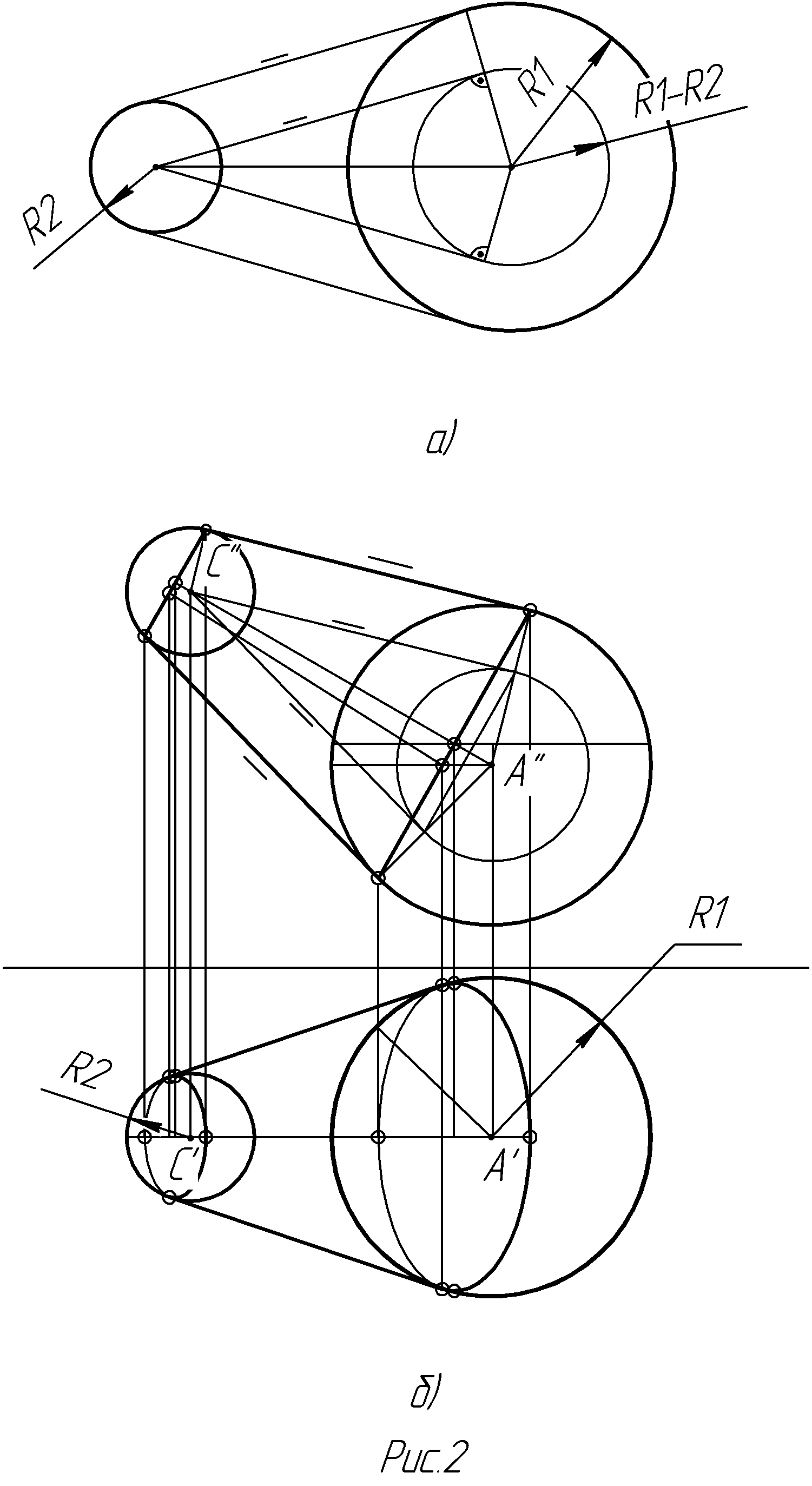
Вспомним задачу из курса средней школы: построить касательную к двум окружностям (рис.2а). Применим оператор РВС. Начнем уменьшать обе окружности на одну и ту же величину. В пределе меньшая окружность превратится в точку, а радиус второй станет равным R1-R2. Через точку, не лежащую на окружности легко провести касательную к окружности. Соединяем точку с центром сферы и строим треугольник, в котором известны две стороны (расстояние от точки до центра сферы и радиус сферы) и прямой угол. Вернемся к исходным данным задачи - все касательные будут параллельны друг другу. Следовательно, проводим касательную параллельную найденной.
Изменим размерность задачи - перейдем к трехмерной постановке: требуется построить огибающую поверхность к двум сферам. Действуем аналогично - уменьшаем радиусы сфер до тех пор, пока меньшая сфера не обратится в точку, затем проводим касательные ко второй измененной сфере, как и в плоском случае. Но необходимо отметить, что такую процедуру мы можем провести только на фронтальной проекции, потому что общая плоскость симметрии этих поверхностей параллельна именно этой плоскости проекции. Затем продлеваем радиус и через точку пересечения с первоначальными размером сферы проводим касательные параллельные найденным в пределе. Горизонтальную проекцию касательных достраиваем по принадлежности соответствующим сферам (см. Рис.2б).
Подобные эксперименты в чем-то субъективны - тут многое зависит от силы воображения, от характера задачи и от других обстоятельств. Однако даже формальное выполнение этих операций резко сбивает психологическую инерцию. Общие рекомендации: а) каждый эксперимент надо вести до появления нового качества, б) каждый эксперимент, чтобы не пропустить появления нового качества, разбивается на шаги; шаг - это изменение параметра объекта на порядок (т.е. в 10 раз).
Оператор РВС не предназначен для получения ответа. Он должен только расковать мысль для дальнейшего продвижения к принципиально новому ответу.
Оператор РВС - это и инструмент по развитию воображения. Десяток задач, пропущенных через него, заметно меняет стиль мышления, более уверенно преодолевается психологическая инерция, обостряется «чутье» на оригинальные идеи. Основной бастион психологической инерции - это старый образ объекта. Чем дальше удастся оторваться мысли от гипнотизирующего образа, тем больше надежды найти принципиально новое решение.
После обработки задачи оператором РВС нужно выявить и устранить техническое противоречие (ТП), использовать вепанализ и другие инструменты ТРИЗ.
В ТРИЗ существует такое понятие, как веполь (от слов «вещество» и «поле») - минимальная техническая система. Объект не может осуществить требуемого действия сам по себе. Он должен взаимодействовать с внешней средой [5]. При этом любое изменение сопровождается выделением, поглощением или преобразованием энергии. Каждый раз, когда дано вещество, приходится добавлять второе вещество и поле. Чтобы поле через второе вещество воздействовало на первое вещество или, наоборот, чтобы первое вещество через второе давало на выходе поле, несущее информацию. В ТРИЗ существует такое правило: невепольные системы (один элемент - вещество или поле) или неполные вепольные системы (два элемента) необходимо для повышения эффективности и управляемости достраивать до полного веполя (три элемента - 2 вещества и поле).
При решении задач начертательной геометрии не используются поля и вещества, однако, попробуем провести аналогию - заменим 2 вещества на 2 объекта, а поле - на посредник между двумя объектами. В этом случае «минимальная техническая система» связывает два объекта при помощи посредника. Вспомним задачу о нахождении второй проекции точки, принадлежащей поверхности. Техническое противоречие - в условии задачи отсутствует связь между двумя объектами точкой и поверхностью. Решение задачи - достройка веполя - вводим посредник - линию, принадлежащую поверхности и проходящую через заданную точку, находим вторую проекцию линии и отмечаем на ней вторую проекцию точки.
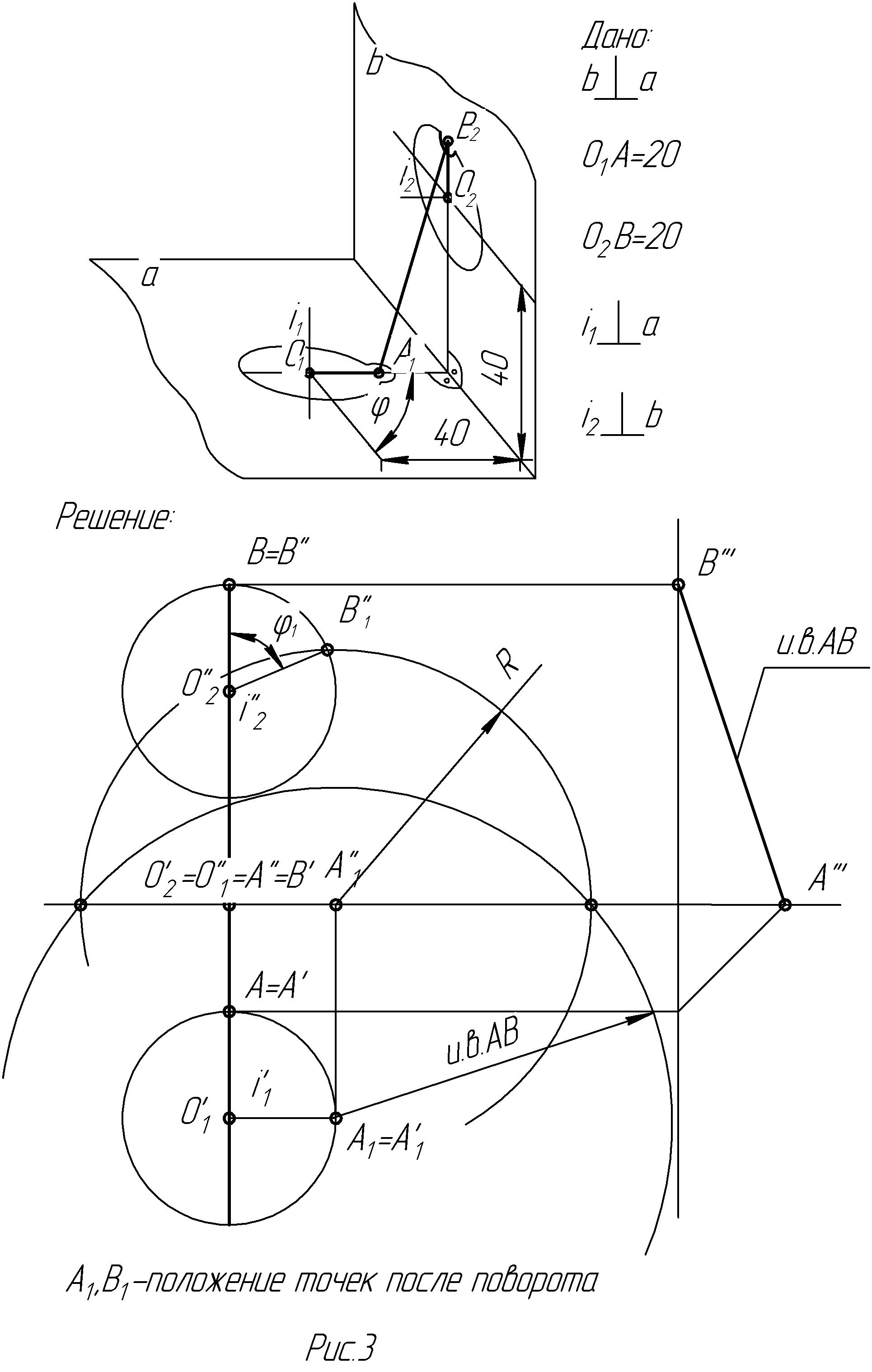
Задача 2. Дан трехзвенный механизм. Звенья О1А и О2В вращаются соответственно вокруг осей i1 и i2 и связаны между собой шатуном АВ (в точках А и В имеются сферические шарниры). На рис.3 показано исходное положение звеньев. Определить угол поворота звена О2В заданного механизма, если звено О1А поворачивается на угол φ=90°.
Для начала приведем условие задачи к удобному для нас графическому виду - введем три плоскости проекций. В первый момент времени нам все известно - положение точек А и В, длина каждого звена. Во второй момент времени - известно положение точки А1. При этом если проанализировать условие задачи, точка В1 может быть двигаться только по окружности, принадлежащей плоскости π2. Можно считать, что звено АВ нерастяжимое, следовательно, его длина, равная истиной величине расстояния от точек А до В, не меняется. Вспомним решение задачи 1 - там дано расстояние от лазера до ракеты. Здесь дано АВ. Найдем все возможные точки отдаленные от А1 на расстояние l (сфера с радиусом l =и.в. АВ и с центром в точке А1). Дальнейшее очевидно - ищем пересечение сферы с плоскостью π2 , а затем с окружностью, по которой двигается точка В и находим В1.
В тот момент, когда решение приходит в голову вся задача озаряется и в ней все становится понятно. Бывает правда преждевременное озарение. В этом случае человек испытывает подсознательную неудовлетворенность. Эту неудовлетворенность необходимо каким-то образом конкретизировать. Попытаться ответить на вопрос: Почему вам не нравится решение? Проверить все ли условия задачи были задействованы в ходе решения. Можно было бы на этот случай привести массу примеров, особенно когда студент пытается решать задачу стандартным способом, а уровень его знаний не позволяет оценить полученный результат.
Хочется надеяться, что на представленных примерах нам удалось показать один из путей развития рефлексии в курсе начертательной геометрии с привлечением идей ТРИЗ.
1. Рубинштейн С.Л. О мышлении и путях его исследования. М., АПН СССР, 1985.
2. Педагогика и логика. М., Касталь, 1993.
3. Давыдов В.В. Теория развивающего обучения. М., 1998.
4. Вербицкий А.А., Пучкова Е.Б. Возможности теста как средства диагностики качества образования: мифы и реальность. Высшее образование в России №6, 2013.
5. Альтшуллер Г.С. Творчество как точная наука. М.: Сов. Радио, 1971
6. Д. Пойа. Математическое открытие. М.: Наука. 1976

Лепаров Михаил Николаевич (21 февраля 2015 г. 22:18) |
Уважаемая Мария Валентиновна, Очень интересный подход! У меня вопрос:Это концептуальная работа или она уже отработана (опыт применения есть)? С уважением
млепаров |

Горнов Александр Олегович (22 февраля 2015 г. 13:48) |
Мария Валентиновна, здравствуйте !
…. Спасибо за интересный доклад! Ваши надежды вполне оправдались…. И идея, и реализация понятны. Подобные методические новации, по нашему мнению, формируют элементы проектных и деятельностных навыков и умений (если угодно, компетенций) и соответствующей ментальности у обучаемых, а это важнее всего. Их прикладная формулировка это элемент, так необходимой, междисциплинарности. Имеем опыт формулировки задач, содержащих в рамках ГГП элементы деятельностной логики…. Но не в фазе выбора способа решения (моделирования ситуации), а конечного результата, при наличии работоспособных альтернатив при оценке их показателей качества, предполагающих геометрические характеристики.
Главный вопрос в таких, безусловно, прогрессивных подходах, насколько их удастся реализовать в практике группового обучения и в индивидуальном формате заданий. Нужны помощники - единомышленники и резервы учебного времени. Желаем развивать Вашу работу, увлечь ею коллег.
С уважением, А.О.Горнов, Л.А. Шацилло
|

Ракитская Мария Валентиновна (22 февраля 2015 г. 22:46) |
Уважаемые Михаил Николаевич, Александр Олегович, Людмила Анатольевна, концептуально эту идею мы с Д.Е.Тихоновым-Бугровым вынашивали давно, в тот период, когда интерес к работе Альтшуллера в нашей стране начал падать, а за рубежом проявляли большой интерес. Однако, с реализацией возникли проблемы: пропал электив по изобретательству (его читали специалисты патентного отдела), не совсем было понятно как вписать всё это в традиционный курс. Я отвечаю на кафедре за работу с продвинутыми студентами и подготовку к олимпиаде по начертательной геометрии, которая проходит в нашем городе с 1979г. В систему подготовки таких студентов элементы ТРИЗ я включаю. |

Лепаров Михаил Николаевич (23 февраля 2015 г. 0:13) |
Здравствуйте, уважаемая Мария Валентиновна! Спасибо за ответ. Я надеюсь, что на конференцию в следующем году Вы познакомите нас с результатом- методологию преподавания, сравнение с традиционному, воспринимания со сторону студентов, проблемы.
Желаю удачи
Пожалуйста, извините мой русский С уважением М.Лепаров |

Ракитская Мария Валентиновна (23 февраля 2015 г. 14:28) |
Спасибо! Буду стараться! |
|
Принцев Николай Владимирович (25 февраля 2015 г. 21:38) |
Дорогая Мария Валентиновна! С огромным интересом прочитал Ваш доклад! Чувствуется Мудрое влияние Дмитрия Евгеньевича Тихонова-Бугрова. Полностью с Вами согласен! |

Шахова Алевтина Бруновна (26 февраля 2015 г. 20:39) |
Здравствуйте Мария Валентиновна, спасибо за доклад, у меня вопрос как я поняла вы отрабатываете теорию ТРИЗ при решение задач НГ повышенной сложности , при подготовке студентов к олимпиадам, а как данная теория применяется в работе с основным контингентом , не обремененным большим интелектуальным уровнем? Есть ли практика применения теории ТРИЗ в курсе ИГ? С уважением Шахова А.Б. |

Гирш Антон Георгиевич (27 февраля 2015 г. 19:31) |
Уважаемая Мария Валентиновна, спасибо за интересный доклад! Приветствую попытки ввести в высшей школе осмысленный подход к решению задач с привлечением элементов мозгового штурма в противовес, или в дополнение, к шаблонному освоению графических методов решения типовых задач. Конечно, одно другое не исключает, но под такой подход нужны учебные часы, которых нет. На Западе в технических Уни упразднили черчение, но есть курс "Основы конструирования", который можно было бы наполнить такого рода методическими подходами. Тут такие имена как Альтшуллер и Пойа востребованы. Эти подходы востребованы и при подготовке членов олимпиадных команд. В своё время в СибАДИ (Омск) для решения конструктивных задач мы вводили так называемые принципы, переводящие каждое элементарное требование задачи в поверхность. Решение достигалось в пересечении поверхностей. Была даже написана методичка "КАК РЕШИТЬ ЗАДАЧУ – Омск: СибАДИ, 1986. Приятно видеть, что Вы владеете материалом. Ваш посев даст всходы. С пожеланием успехов. А.Г.Гирш. |

Ракитская Мария Валентиновна (28 февраля 2015 г. 8:38) |
Уважаемый Антон Георгиевич, спасибо за внимание к докладу и добрые пожелания. Очень интересна идея решения конструктивных задач. К некоторым задачам мы такой подход использовали. Хотелось бы ознакомиться с этой методичкой. М.В.Ракитская |

Ракитская Мария Валентиновна (28 февраля 2015 г. 8:54) |
Уважаемая Алевтина Бруновна, здравствуйте! Долго собиралась Вам ответить. Подробный ответ на Ваш вопрос содержится в моём ответе профессорам Лепарову и Горнову (см. выше). Добавлю следующее: у нас на кафедре развита такая форма работы со студентами, как СРС (самостоятельная работа студента под руководством преподавателя) - своего рода дополнительные занятия, где каждый преподаватель два раза в неделю помогает студенту осваивать изучаемые предметы. При ответе на вопросы студентов часто необходимо снимать "инерцию" терминов, переходить от решения задачи в пространстве к задаче в двумерной постановке. Что касается практики применения ТРИЗ в курсе ИГ, хотелось бы сказать, что подспудно все мы ее элементы применяем. Например, при оценке работоспособности конструкции часто определяется минимальная толщина стенки и, если она не удовлетворительная, то студенту приходится разрешать противоречие: увеличивать ли наружный диаметр или уменьшать отверстие, или придумать еще что-нибудь. Также к изобретательским задачам можно отнести любую конструктивную сложность (противоречие): подбор шага резьбы, использование проточки или недореза, выбор оптимальной шероховатости, "облегчение" конструкции и т.д. М.В. Ракитская |

Дударь Елена Сергеевна (1 марта 2015 г. 10:04) |
Уважаемая Мария Валентиновна! С большим интересом прочитала Ваш доклад. Всегда радует, что в современных реалиях существуют и совершенствуются идеологии системного подхода для развития инновационного обучения. Идеи ТРИЗ, зародившись в России, сейчас широко популярны за рубежом. Высылаю Вам адрес online shop (www.triz.guru), где представлено несколько современных книг по данной тематике. Мне приглянулась «Инженерно-техническое творчество в нефтегазовой отрасли. Сборник задач», авторы Ёлкин С.В., Гаврилов Д.А. Сайт на английском языке, посвящен, прежде всего, направлению BioTRIZ (UK, University of Bath, www.biotriz.com). Полагаю, что существуют и другие последователи ТРИЗа, так как в этой области накоплен огромный опыт именно педагогического характера - начиная от дошкольников, и кончая взрослыми людьми... Кроме того, есть разделы ТРИЗа, которые специально разработаны не для инженерных, а для исследовательских, чисто научных задач... Всецело поддерживаю Ваши начинания. С наилучшими пожеланиями, Елена Дударь |

Ракитская Мария Валентиновна (2 марта 2015 г. 18:19) |
Уважаемая Елена Сергеевна, большое спасибо за внимание к моей работе. Для меня это особенно ценно т.к. я знаю, что Вы хорошо осведомлены о проблемах высшего образования за рубежом. В свою очередь рекомендую книгу М.Меерович, Л.Шрагина Теории решения изобретательских задач, рассчитанную на широкую аудиторию, начиная со школьников. М.В. Ракитская |

Ракитская Мария Валентиновна (2 марта 2015 г. 19:29) |
Хотела бы поблагодарить Дмитрия Евгеньевича Тихонова-Бугрова, потому что без него и статьи бы не было, и он мне во всем помогает. А я человек пока неопытный, и простите меня за это. М.В. Ракитская |

Дударь Елена Сергеевна (2 марта 2015 г. 23:57) |
Добрый день, Мария Валентиновна! Благодарю за ссылку на книгу. Мне нравится формат этой конференции именно за возможность непосредственного общения с коллегами. Это важно, когда находятся единомышленники, когда на «мои вопросы» кто-то уже нашел ответы. Долгое время я занималась подготовкой студентов к олимпиадам по начертательной геометрии, тоже искала инструменты (общие подходы) к решению нестандартных задач. Это мне и сейчас интересно. Однако, Вы затронули еще один важный вопрос психологии и педагогики - это слабое развитие рефлексии учащихся. Для меня термин «рефлексия» какой-то «не очевидный», сложный. Не являясь специалистом в данном вопросе, могу лишь косвенно предположить, что означает фраза «сама деятельность становится предметом специальной обработки, чтобы на неё направилась бы новая, вторичная деятельность». Это цитата, оставим её в покое… А вот перечень умений для рефлексивного анализа мне показался актуальным. Думаю, что в практике обучения важно о нем помнить. Пробовали ли Вы, используя знания по психологии учащихся и инструменты ТРИЗа, заниматься с отстающими студентами? Насколько это эффективно? У меня часто бывает, что «вытаскиваю» студента по своему предмету, а по другим его уже отчисляют. С уважением, Елена Дударь. P.S. Просто замечательно, что у Вас такие наставники как Дмитрий Евгеньевич. Доклад действительно интересный. |

Ракитская Мария Валентиновна (3 марта 2015 г. 18:04) |
Здравствуйте, Елена Сергеевна. Очень рада снова встретиться с Вами. Ситуация, описанная Вами, очень знакома. Что касается отстающих. Они приходят на СРС регулярно. Заметила, что эффект может дать Альтшуллеровский принцип гашения психологической инерции. Говоришь студенту: путаешься в терминах? Давай называй всё по своему и в своих терминах давай пространственную идею решения. Часто срабатывает. С уважением, М. Ракитская. |

Тихонов-Бугров Дмитрий Евгеньевич (4 марта 2015 г. 11:02) |
Уважаемые коллеги, с большим интересом узнал, что принцип гашения психологической инерции (принцип переформулировки) с успехом применял в своей практике А.Г.Гирш (Как решить задачу. СибАДИ, 1986). Большое спасибо, Антон Георгиевич. Тихонов-Бугров. |