Бойков Алексей Александрович

|
Город: Иваново
Организация: Ивановский Государственный Энегретический Университет им. В.И.Ленина
Отрасль науки: технические науки
Список публикаций автора в РИНЦ
Ссылка на публикации в предыдущих конференциях КГП
Список опубликованных докладов:
- АВТОМАТИЗАЦИЯ ПРОВЕРКИ ИНЖЕНЕРНО-ГРАФИЧЕСКИХ ЗАДАНИЙ, Бойков Алексей Александрович
- ВЕРИФИЦИРУЕМОСТЬ ИНЖЕНЕРНО-ГРАФИЧЕСКИХ ЗАДАЧ КАК НЕОБХОДИМОЕ УСЛОВИЕ ЭФФЕКТИВНОЙ САМОСТОЯТЕЛЬНОЙ РАБОТЫ, Бойков Алексей Александрович
Список комментариев:
|
Круглый стол по обсуждению проекта решения конференции, (28 марта 2016 г. 15:23) |
Уважаемые коллеги! Хочу выразить огромную благодарность организаторам конференции и лично Ирине Дмитриевне! Для меня эти недели (с поправкой на ежедневную занятость) были как возможность выбраться из Иванова для физического участия в конференции или ФПК. Поддерживаю основные решения конференции. Благодарю всех участников за интересные доклады, за много новых мыслей, за обмен мнениями и общение! Желаю всем здоровья, способных студентов, научных и педагогических успехов! С уважением, Бойков. |
|
ЖУРНАЛ «ГЕОМЕТРИЯ И ГРАФИКА» СЕГОДНЯ: СТАТУС ВАКОВСКОГО ИЗДАНИЯ, Сальков Николай Андреевич (25 марта 2016 г. 18:54) |
Уважаемые Николай Андреевич и Владимир Игоревич! Я и мои коллеги с кафедры графики ИГЭУ присоединяемся к оценкам и пожеланиям и выражаем глубокую благодарность за Ваш колоссальный труд, за появление, "становление" и постоянное развитие и улучшение единственного в стране геометро-графического журнала. С уважением, А.А. Бойков и коллектив кафедры КиГ. |
|
К ПЯТИЛЕТНЕМУ ЮБИЛЕЮ КОНФЕРЕНЦИИ ПО КАЧЕСТВУ ГЕОМЕТРО-ГРАФИЧЕСКОЙ ПОДГОТОВКИ (КГП): ДО И ПОСЛЕ ОЧЕРЕДНЫХ ДИСКУССИЙ, Горнов Александр Олегович (23 марта 2016 г. 22:08) |
Уважаемый Александр Олегович, а где найти эти замечательные сборники материалов? Можно ли приобрести, в частности, сборник, который будет издан по результатам КГП2016? С уважением, Бойков. |
|
ЧЕТЫРНАДЦАТАЯ ВСЕРОССИЙСКАЯ СТУДЕНЧЕСКАЯ ОЛИМПИАДА ПО НАЧЕРТАТЕЛЬНОЙ ГЕОМЕТРИИ, ИНЖЕНЕРНОЙ И КОМПЬЮТЕРНОЙ ГРАФИКЕ, Вышнепольский Владимир Игоревич (23 марта 2016 г. 21:33) |
Здравствуйте, Владимир Игоревич! Рад новой встрече! Разрешите выразить Вам и кафедре глубокую признательность за титанический труд по организации и проведению олимпиады, тем более, что с каждым годом число участников только растет! С уважением, Бойков. |
|
ГРАФИЧЕСКИЕ ЗАДАЧИ ПРИ ПРОЕКТИРОВАНИИ НАДУВНЫХ КОНСТРУКЦИЙ, Дюмин Владимир Андреевич, Семёнов Виктор Алексеевич, Тихонов-Бугров Дмитрий Евгеньевич (23 марта 2016 г. 21:28) |
Уважаемые Дмитрий Евгеньевич, Владимир Андреевич и Виктор Алексеевич, спасибо за высокую оценку и поддержку! Пожелания А.М. Федотову передам. С уважением, Бойков. |
|
ФОНД ОЦЕНОЧНЫХ СРЕДСТВ КАЧЕСТВА ГРАФИЧЕСКОЙ ПОДГОТОВКИ, Александрова Евгения Петровна, Кочурова Людмила Владимировна, Крайнова Марина Николаевна, Столбова Ирина Дмитриевна (23 марта 2016 г. 21:13) |
Уважаемые коллеги, спасибо за доклад! ФОСы - весьма актуальная для нас сейчас тема, а опыт коллег по стране - неоценим. С уважением, Бойков. |
|
АВТОМАТИЗАЦИЯ ПРОВЕРКИ ИНЖЕНЕРНО-ГРАФИЧЕСКИХ ЗАДАНИЙ, Бойков Алексей Александрович (23 марта 2016 г. 0:11) |
Уважаемые Александр Олегович и Людмила Анатольевна, спасибо за высокую оценку и поддержку! С уважением, А.А.Бойков. |
|
ГРАФИЧЕСКИЕ ЗАДАЧИ ПРИ ПРОЕКТИРОВАНИИ НАДУВНЫХ КОНСТРУКЦИЙ, Дюмин Владимир Андреевич, Семёнов Виктор Алексеевич, Тихонов-Бугров Дмитрий Евгеньевич (22 марта 2016 г. 23:40) |
Уважаемые коллеги, спасибо за замечательный доклад и отличные примеры! Давно думаю о том, чтобы на своем потоке организовать групповую работу, но пока, к сожалению, не нашел подходящих проектов. С уважением, Бойков. |
|
ИСПОЛЬЗОВАНИЕ РАКЕТНО-КОСМИЧЕСКОЙ КОМПОНЕНТЫ В ГРАФИЧЕСКОЙ ПОДГОТОВКЕ В СИСТЕМЕ ШКОЛА-ВУЗ, Абросимов Сергей Николаевич, Пахомова Ольга Фёдоровна, Тихонов-Бугров Дмитрий Евгеньевич, Уханёва Вера Андреевна (22 марта 2016 г. 23:06) |
Уважаемые коллеги, спасибо за интересный доклад. Работы впечатляют и очень радуют. Я давно пришел к выводу, что первую часть начертательной геометрии (точки, прямые и плоскости) уже давно пара перенести в школьный курс и изучать вместе со стереометрией. Тогда в вузах можно было бы успешно заниматься "высшей" начертательной геометрией - преобразованиями, образованием поверхностей и др. Увы, пока об этом можно только мечтать. С уважением, Бойков. |
|
ВЕРИФИЦИРУЕМОСТЬ ИНЖЕНЕРНО-ГРАФИЧЕСКИХ ЗАДАЧ КАК НЕОБХОДИМОЕ УСЛОВИЕ ЭФФЕКТИВНОЙ САМОСТОЯТЕЛЬНОЙ РАБОТЫ, Бойков Алексей Александрович (22 марта 2016 г. 22:58) |
Уважаемый Денис Вячеславович, буду признателен за любую информацию. Несколько лет назад я дошел до необходимости использовать что-то вроде геометрического Пролога для автоматизации проверки, но из-за отсутствия подходящих редакторов был вынужден заняться их разработкой. С уважением, Бойков. |
|
АВТОМАТИЗАЦИЯ ПРОВЕРКИ ИНЖЕНЕРНО-ГРАФИЧЕСКИХ ЗАДАНИЙ, Бойков Алексей Александрович (22 марта 2016 г. 22:52) |
Уважаемый Александр Львович, спасибо внимание к моей работе и добрые пожелания! Я очень рад, что в этом вопросе наши точки зрения совпадают. Работая над докладом, я припомнил, будто видел статью, где давались временные оценки советского периода, сколько времени на проверку заданий тратил преподаватель. Пересмотрел мои архивы - сборники НГиИГ, некоторые выпуски "Прикладной геометрии..." - нашел только оценку труда студентов при решении. При нынешнем базовом образовании необходимость дополнительной проверки только возрастает. Рост объема проверки ведет к уменьшению числа решаемых задач. В нашей тетради - около сотни простых заданий (в том же Фролове - почти триста). Но даже это - колоссальное время, - Ваши цифры это наглядно показывают. Мы проверить все задачи у всех студентов просто не в силах, проверяем только ключевые, а по остальным работаем, по сути, только с теми студентами, кто сам задает вопросы. Насчет проверки в AutoCAD'е. В первой части доклада упоминается, что мы поставили задачу не только автоматизировать проверку, но и реализовать проверку в связке с Интернет-системой. Это накладывает дополнительные ограничения: проверка должна осуществляться на стороне сервера. Вы совершенно правы насчет неудобств DXF. Отдельное спасибо за ссылки. С уважением, А.А.Бойков. |
|
АВТОМАТИЗАЦИЯ ПРОВЕРКИ ИНЖЕНЕРНО-ГРАФИЧЕСКИХ ЗАДАНИЙ, Бойков Алексей Александрович (22 марта 2016 г. 22:33) |
Уважаемый Сергей Игоревич, спасибо за высокую оценку! Хочу отдельно поблагодарить моего научного руководителя А.М. Федотова. Надеюсь выступить с докладом в апреле. С уважением, А.А.Бойков. |
|
ВЕРИФИЦИРУЕМОСТЬ ИНЖЕНЕРНО-ГРАФИЧЕСКИХ ЗАДАЧ КАК НЕОБХОДИМОЕ УСЛОВИЕ ЭФФЕКТИВНОЙ САМОСТОЯТЕЛЬНОЙ РАБОТЫ, Бойков Алексей Александрович (17 марта 2016 г. 23:36) |
Алексей Алексеевич, вряд ли я Вам серьезно помогу. Сам я имею опыт программирования AutoCAD только на AutoLISP. Мое недовольство этим диалектом связано не с автокадом, а с тем, что AutoLISP во многом противоречит идеологии функционального программирования Lisp вообще. Автокад поддерживает несколько технологий программирования - AutoLISP, VB, VBA, VB.NET, C++, C#. Некоторым из них периодически пророчат устарение и умирание, но, учитывая число пользователей по всему миру, думаю, до этого не дойдет. На сайте Autodesk (2012 год) про это ни слова http://www.autodesk.ru/adsk/servlet/item?siteID=871736&id=18221924 . С уважением, Бойков. |
|
ВАРИАТИВНОСТЬ РЕШЕНИЯ ЗАДАЧ НАЧЕРТАТЕЛЬНОЙ ГЕОМЕТРИИ, Глазунов Константин Олегович, Лызлов Александр Николаевич (17 марта 2016 г. 22:55) |
Уважаемые Александр Николаевич и Константин Олегович, Вы делаете большое дело, и то, что Вы делитесь своим опытом, тоже очень важно. Доклад замечательный, я точно возьму кое-что на вооружение. Что касается загрузки детей, я наблюдал за своей специальностью, хотя непосредственно НГ я у них не читаю, но на втором курсе мы с ними занимаемся алгоритмами машинной графики. Разговаривая о том, что и как они изучают, что успевают, и вспоминая себя в их возрасте, я пришел к выводу, что все-таки у меня было больше свободного времени. В частности, я каждый день мог позволить себе час-два программировать "для души" и даже еще посещал кружки, а они, такое ощущение, что все время только выполняют домашние задания. Может быть, причина в том, что они хуже подготовлены, и те задачи, которые у меня требовали полчаса, отнимают у них часы. Впрочем, могу ошибаться, спорить не стану. |
|
ГЕОМЕТРИЧЕСКАЯ ПОДГОТОВКА БАКАЛАВРОВ В УСЛОВИЯХ УХОДА КЛАССИЧЕСКОГО ЧЕРТЕЖА ИЗ СОВРЕМЕННОГО ВЫСОКОТЕХНОЛОГИЧНОГО ПРОИЗВОДСТВА, Соколова Людмила Сергеевна (17 марта 2016 г. 18:29) |
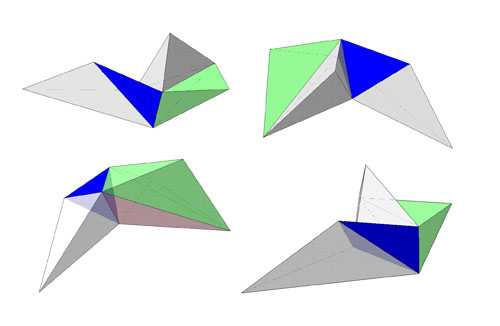
Уважаемая Людмила Сергеевна, прошу прощения за въедливость, но мне хочется кое в чем разобраться до конца. Хоть я и "не знаю, не видел, не изучал", но многомерная геометрия меня интересует, кстати, благодаря Геннадию Сергеевичу Иванову, который на курсах повышения квалификации в МВТУ прочитал нам (слушателям) лекцию о многомерной геометрии. Г.С. решал задачу пересечения прямой с гиперплоскостью, не помню, то ли в 4х-, то ли в 5ти- мерном пространстве, используя для этого ортогональный чертеж. До того случая я многомерной геометрией не интересовался, а после лекции у меня в руках вдруг оказался простой и эффективный инструмент для исследования многомерных фигур и решения некоторых задач - хорошо знакомый мне комплексный чертеж, никак не изменившийся по сравнению с 3D, кроме появления еще одной проекции. И тут Ваш доклад с многомерной геометрией в 3D. Я самым честным образом пытаюсь понять Ваши основные тезисы. Я тут набросал на досуге пример. Дана трехмерная развертка четырехмерной фигуры общего вида (искал ракурс как можно выгоднее). Что можно сказать об исходной фигуре?
Что нам это дает? Какие это открывает перед нами возможности? Можем ли мы построить произвольное трехмерное сечение? Двухмерное? Как мы будем развертывать пятимерную фигуру, если уже развертка сама будет четырехмерной? С уважением, Бойков. |
|
ВЕРИФИЦИРУЕМОСТЬ ИНЖЕНЕРНО-ГРАФИЧЕСКИХ ЗАДАЧ КАК НЕОБХОДИМОЕ УСЛОВИЕ ЭФФЕКТИВНОЙ САМОСТОЯТЕЛЬНОЙ РАБОТЫ, Бойков Алексей Александрович (17 марта 2016 г. 17:40) |
Уважаемый Александр Львович, я полностью согласен с Вами в том, что трехмерная геометрия - это очень хорошо, и что решать задачи трехмерного моделирования с использованием 3D-пакетов полезно и нужно. Вашу книгу 2002 года я неоднократно давал ребятам с факультета информатики для углубления знаний Автокада, в том числе для знакомства с AutoLISP'ом. Тем не менее, я не считаю, что изучать Lisp (тем более, диалект AutoLISP) - первоочередная задача геометрического образования. Программировать геометрические задачи можно в Python (Компас) или сразу в C++ (он тоже стыкуется с некоторыми пакетами), неважно. Я вижу цель геометрического образования в изучении геометрии, и чем меньше будет посредников, тем лучше. Я позволю себе продолжить Вашу аналогию. Если "развивать формальное мышление следует на современных примерах и 3d задачах" в системе AutoCAD, тогда всю высшую математику давно пора переводить на MathCAD, MathLab, а еще лучше сразу на Mapple или Mathematica, и перестать уже решать типовые расчеты - брать производные, интегралы, считать матрицы, преобразовывать выражения и выполнять прочие работы "вчерашнего дня". Современные специалисты должны решать современные задачи, и им вовсе не обязательно знать и задумываться, как работают их инструменты. С уважением, Бойков. |
|
ВЕРИФИЦИРУЕМОСТЬ ИНЖЕНЕРНО-ГРАФИЧЕСКИХ ЗАДАЧ КАК НЕОБХОДИМОЕ УСЛОВИЕ ЭФФЕКТИВНОЙ САМОСТОЯТЕЛЬНОЙ РАБОТЫ, Бойков Алексей Александрович (17 марта 2016 г. 17:20) |
Уважаемые Дмитрий Евгеньевич и Николай Андреевич, спасибо! Я очень рад, что наши мнения в этом вопросе совпадают. |
|
ГЕОМЕТРИЧЕСКАЯ ТОЧНОСТЬ КОМПЬЮТЕРНЫХ АЛГОРИТМОВ КОНСТРУКТИВНЫХ ЗАДАЧ , Хейфец Александр Львович (17 марта 2016 г. 12:59) |
Уважаемый Александр Львович, спасибо за доклад! Приведен обзор интересных задач и экспериментов. Полученные Вами результаты, в принципе, ожидаемы и не вызывают сомнения. К сожалению, в постановке задачи, и, следовательно, в выводах мне хотелось бы внести необходимые уточнения. >> Недоверие к компьютерной геометрической точности сторонники НГ используют как аргумент против активного перехода к 3D методам в учебном процессе Во-первых, геометрическая точность, к которой аппелируют сторонники конструктивной геометрии, имеет ценность не в прикладном, а в теоретическом, т.е. сугубо научном отношении. Например, практика вычислений показывает, что компьютерная реализация численного решения уравнения четвертого порядка работает быстрее, чем вычисления в радикалах (к сожалению, не могу привести источник, но идея состоит в том, что итерационные вычисления можно свести к быстрым арифметическим операциям). Отменяет ли это теоретическую ценность "точного" решения? Не стоит ли нам всю математику перевести на итерационные методы? Конструктивная геометрия циркуля и линейки имеет, в первую очередь, такую же теоретическую ценность, поскольку конкретная реализация алгоритма сведется к построению прямых и окружностей в AutoCAD'е или Компасе, геометрические ядра которых работают на численных методах. Не меньшую теоретическую ценность имеет геометрия сфер и плоскостей (впрочем, и любых других фигур - 3-, 4- и более высоких порядков) в трехмерном пространстве, 4-гиперсфер и 4-гиперплоскостей в четырехмерном и тп, если только мы будем решать задачи конструктивно и/или аналитически, а не перекладывать все на численные методы вычислений. Поэтому теоретическое решение средствами начертательной геометрии или трехмерного моделирования одинаково точны, а решения при помощи окружностей или сфер в Компасе - одинаково приближенны. Предположим, мы получили в решении n точек плоской фигуры, каждые 5 из которых при вычислении коэффициентов уравнения второго порядка дают одну и ту же конику. Можем ли мы утверждать, что нашли кривую второго порядка? Нет. Это останется лишь рабочей гипотезой, пока не будет найдено аналитическое или конструктивное доказательство, потому что может статься, мы нашли кривую, очень похожую на кривую второго порядка в пределах 8-10 знаков после запятой. Поэтому, >> Компьютерные 3D методы, особенно 3D параметризация, позволяют достаточно просто исследовать геометрические закономерности задач. - на уровне гипотез, которые, в свою очередь, также требуют проверки и доказательства. >> Методы 3D лежат в основе современных САПР и активно развиваются. В отличие от НГ, они являются актуальными и перспективными. Обучение им уже в первом семестре готовит студентов к освоению современных методов проектирования и геометрического моделирования Несомненно. В то же время начертательная геометрия показывает, что задачи, которые решаются на сферах и плоскостях (на гиперсферах и гиперплоскостях) могут быть сведены к окружностям и прямым, а это очень простые инструменты. Простые инструменты позволяют исследовать сложные геометрические формы. Не забывайте о неевклидовых геометриях, о комплексных координатах и т.д. - областях, без которых невозможно представить современную геометрию, и которые затруднительно моделировать в Компасе, AutoCAD, Inventor и др., но вполне возможно при помощи циркуля и линейки, если знать, как. Поэтому, (мой вывод) выпускающие кафедры, очевидно, должны достаточно времени уделять изучению современных инструментов прикладного геометрического моделирования. Фундаментальное геометрическое образование здесь не при чем. Это, конечно, идеальная ситуация. В реальности нас могут обязать учить трехмерным пакетам вместо геометрии, но уж стремиться к этому самим, я считаю, мы никак не должны. >> На студентов оказывает влияние и фактор эмоционального восприятия сопоставляемых алгоритмов. Вместо набора множества линий, карандаша и бумаги, которые до сих пор в учебном процессе остаются основными инструментами НГ, решение 3D – это современные компьютерные технологии, цвет, фотореалистичность. И, как следствие, неумение теоретизировать и проверять, если только в компьютерной программе нельзя рассмотреть предмет со всех сторон или выполнить измерения при помощи стандартного инструмента, т.е. мы будем учить студентов считать доказательством первичную оценку правильности гипотезы. >> Точность геометрических построений необходимо определять не по абстрактным критериям применения циркуля и линейки, а по реальной погрешности построений, которую можно измерить и сравнить с требуемым значением. В действительности, результат сравнения показывает, что геометрический редактор AutoCAD и вычислительная машина, считающая, к примеру, "a1 = a sin(arctg (sqrt 2))" находят один и тот же результат. Это просто здорово. (Мой вывод - ) В прикладных задачах, мы можем доверять как AutoCAD'у, так и вычислительной машине. При чем здесь точность геометрического решения и геометрия, в целом? с уважением, Бойков. |
|
ГЕОМЕТРИЧЕСКИЙ ФАКУЛЬТАТИВ. ЧЕМ «ОЗАДАЧИТЬ» ЗАИНТЕРЕСОВАННОГО СТУДЕНТА?, Волошинов Денис Вячеславович (17 марта 2016 г. 0:54) |
Денис Вячеславович, буду первым. Спасибо за замечательный доклад! Интересно, свежо, с настоящей геометрией, есть над чем подумать и чему поучиться. |
|
ВЕРИФИЦИРУЕМОСТЬ ИНЖЕНЕРНО-ГРАФИЧЕСКИХ ЗАДАЧ КАК НЕОБХОДИМОЕ УСЛОВИЕ ЭФФЕКТИВНОЙ САМОСТОЯТЕЛЬНОЙ РАБОТЫ, Бойков Алексей Александрович (16 марта 2016 г. 12:04) |
Уважаемый Александр Львович, здравствуйте. Рад снова общаться. Спасибо за внимание к моему докладу и замечания. 1. Что касается терминологии, если мы предполагаем у студента желание научиться, как того подразумевают все образовательные инновации, то любая автоматизированная проверка на стратегическом уровне является самопроверкой. В этом смысле я обобщаю. Предположим, школьник учится умножать в столбик и сверяет свой ответ с решением компьютера - что это? 2. Конкретно в данной работе контроль имел статистические задачи. Карты контроля составлялись преподавателем. Тренажер служит для самоподготовки. Экзамен они все равно сдают преподавателю лично, а на контрольных работах решают задачи. 3. Мое отношение к 3d сугубо положительное - к 3d, 4d, ... Чертеж, я считаю, более удобным инструментом для отработки навыков формальных методов моделирования, а достоинства 3d пакетов проявляются лишь в прикладной области предметного моделирования и автоматизации подготовки конструкторской документации. При использовании AutoCAD'а, если мы захотим чего-то большего, чем стандартные инструменты, мы будем вынуждены браться за LISP. Что далеко выходит за рамки отведенных часов и задач. 4. Спасибо за ссылку на Ваш доклад. В моих основных исследованиях (автоматизация проверки решений задач), я также пришел к автогенерации исходных заданий, но, пока не решена проблема автоматической расстановки обозначений, эта технология применяется мной ограниченно. с уважением, Бойков |
|
ГЕОМЕТРИЧЕСКАЯ ПОДГОТОВКА БАКАЛАВРОВ В УСЛОВИЯХ УХОДА КЛАССИЧЕСКОГО ЧЕРТЕЖА ИЗ СОВРЕМЕННОГО ВЫСОКОТЕХНОЛОГИЧНОГО ПРОИЗВОДСТВА, Соколова Людмила Сергеевна (15 марта 2016 г. 23:36) |
Уважаемый Николай Андреевич, "этот посыл" не заслуживает ответа, в принципе. Мое мнение - чертеж не уйдет, не просто "еще долго", а, думаю, в обозримом будущем или вообще, как не уходят шариковые ручки и бумага, как бумажные книги и еще многое. Очевидно, часть чертежа займут технологии "3D электронного моделирования", часть - трансформируется в электронный чертеж, который будет значительно удобнее бумажного - станет интерактивным, динамическим, многомерным и т.п., думаю, останется и бумажный чертеж, в конце концов, ни один самый большой монитор не сравнится с листом формата А0 или хотя бы А1. В конце концов это просто красиво. С другой стороны, попал ко мне в руки недавно учебник Рынина 1939 года (появится время, выложу там же, с Извольским) - ведь не сравнишь с нынешним Королевым. Ведь это не кто-то "извне" сделал начертательную геометрию "прислужницей", свои же. Измельчали учебники, задачники (ведь все это не нужно для того, чтобы построить чертеж!) - столько всего порастеряли. Теперь пожинаем. С уважением, Бойков. |
|
ВЕРИФИЦИРУЕМОСТЬ ИНЖЕНЕРНО-ГРАФИЧЕСКИХ ЗАДАЧ КАК НЕОБХОДИМОЕ УСЛОВИЕ ЭФФЕКТИВНОЙ САМОСТОЯТЕЛЬНОЙ РАБОТЫ, Бойков Алексей Александрович (15 марта 2016 г. 22:37) |
Уважаемый Дмитрий Евгеньевич, спасибо за высокую оценку! Ваше мнение очень важно для меня, мне памятен пример с шахматами, приведенный Вами в докладе КГП-2011. Ваш доклад и еще Дениса Вячеславовича о "будущем начертательной геометрии" тогда заставил меня иначе взглянуть на происходящее в геометро-графическом образовании. По поводу пособия Павла Григорьевича пусть это будет репликой о книге, как "артефакте". Она передо мной возникла при следующих обстоятельствах. Вместо февральских каникул мы едва ли не всей кафедрой посещали курсы повышения квалификации, на которых нас обрадовали, что программы в этом году придется переделывать дважды (весной и в сентябре). И там же рекомендовали включить в список литературы учебники "Лани", доступные в читальных залах института в электронном виде. В поиске по "начертательной геометрии" и по "инженерной графике" эта книжка - первая или одна из первых. Отношение к интернет-тестированию у меня резкое - вопросы многие поставлены из рук вон плохо, чертежи - ужасные, студенты, используя режим самоподготовки, легко "натаскивают" себя на 3 и 4, а потом благополучно заваливают зачет. И неизвестно, что с ними делать после этого. |
|
ВАРИАТИВНОСТЬ РЕШЕНИЯ ЗАДАЧ НАЧЕРТАТЕЛЬНОЙ ГЕОМЕТРИИ, Глазунов Константин Олегович, Лызлов Александр Николаевич (14 марта 2016 г. 0:58) |
Уважаемые Александр Николаевич и Константин Олегович, спасибо за интересный доклад с хорошими примерами. Полностью поддерживаю вашу точку зрения насчет необходимости изучать разные способы решения задач, в том числе при помощи аффинных и проективных преобразований, дополнительного параллельного и центрального проецирования. Боюсь только, реальных часов на изучение дисциплины в большинстве вузов попросту не хватит, ведь каждый из этих интересных способов требует времени - показать применение, объяснить сущность, попробовать, закрепить. Чтобы был эффект, показать надо не один раз. Ограничено не только число часов в аудиториях, но и часы самостоятельной работы расписаны в РПД. Формально: одно только домашние графические работы требуют многих часов от первокурсников. Физически: у них еще высшая математика, физика, химия... - пятилетняя программа, "сжатая" в четыре бакалаврских года, и более слабая школьная подготовка. Плюс отсутствие материала в учебниках и задачниках основного фонда литературы (последние 5 лет!). Фактически, все это богатство методов остается для факультативов с олимпиадниками. С уважением, Бойков |
|
МНИМЫЕ ЭЛЕМЕНТЫ В АЛГЕБРЕ И ГЕОМЕТРИИ, Короткий Виктор Анатольевич (12 марта 2016 г. 20:03) |
Виктор Анатольевич, здравствуйте! Рад новой встрече. Спасибо за доклад, как всегда, интересный и "геометричный". С уважением, Бойков |
|
К РЕШЕНИЮ ЗАДАЧИ О ТОЧКАХ ПЕРЕСЕЧЕНИЯ КРИВЫХ ВТОРОГО ПОРЯДКА, Волошинов Денис Вячеславович (12 марта 2016 г. 14:49) |
Денис Вячеславович, спасибо за решение в Симплексе, интересно видеть решение новых задач в этом замечательном инструменте, еще раз повторюсь, буду ждать статьи в ГиГ с нетерпением! По поводу касательных коник - была такая идея. Мы можем строить окружность, касательно к трем другим прямым или окружностям. Следующим обобщением было бы рассмотреть построение, скажем, параболы (4 параметра) или эллипса (5 параметров), касательно прямым и окружностям в разных сочетаниях, из которых по крайней мере одна - окружность. Очевидно, там порядки будут высокие, но хотелось хотя бы взглянуть на эту систему уравнений. |
|
ГЕОМЕТРИЧЕСКАЯ ПОДГОТОВКА БАКАЛАВРОВ В УСЛОВИЯХ УХОДА КЛАССИЧЕСКОГО ЧЕРТЕЖА ИЗ СОВРЕМЕННОГО ВЫСОКОТЕХНОЛОГИЧНОГО ПРОИЗВОДСТВА, Соколова Людмила Сергеевна (10 марта 2016 г. 13:10) |
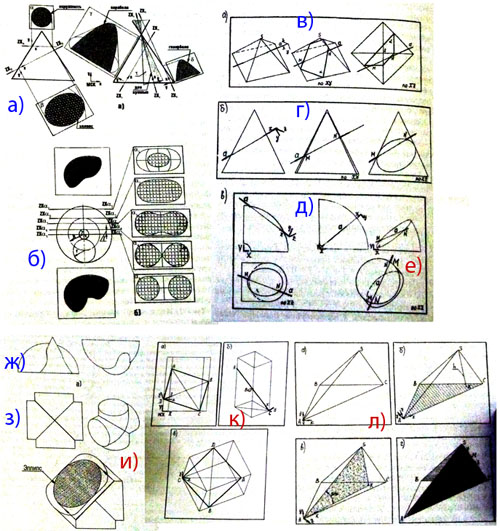
Уважаемая Людмила Сергеевна, по второй ссылке работы С.А. Лапшиной, А.С. Рожкова, к сожалению, найти не смог. Я проглядел статью [1] и вспомнил, что у меня к этой статье были вопросы. В частности, на с. 41 приведена формула расчета размерности пересечения : r = 2+3-2=1 (линия) - должно быть равно 3? В докладе вы ссылаетесь на статью [1]: "была опробована и подтверждена экспериментально возможность встраивания наглядной геометрии и многомерного пространства", но в статье [1] я не увидел ни одного наглядного изображения многомерных фигур, кроме известной развертки тессеракта. Сомневаюсь, что эта развертка наглядно демонстрирует свойства оригинала. Большая часть иллюстраций к статье [1] - именно ортогональные проекции, которые, в соответствии с вашими тезисами, лишены "одной из наиболее привлекательных особенностей геометрии, а именно наглядности изображения". Я позволю себе привести некоторые.
На рис. а и б для указания положения секущей плоскости использованы ортогональные проекции (более наглядны?!), а не аксонометрии. На рис. г, д, ж, з также выбраны ортогональные проекции, и аксонометрические их только дополняют (рис. е, и), причем наглядность последних вызывает у меня сомнения. Сравнительно наглядными я считаю лишь рис. в, к, л, изображающие многогранники. Причина - особенности выпуклых многогранников, а не достоинства аксонометрий. Перпендикулярность высоты основанию ABC в пирамиде на рис. (л.б) неочевидна (не наглядна?). Методика решения графических задач на центральных и параллельных аксонометриях многогранников есть у Вольберга (Лекции по начертательной геометрии), Четверухина (Аксонометрия) и др. Таким образом, я совсем запутался и не понял, какой смысл вы вкладываете в слово "наглядность". Имея в виду объективную и, очевидно, поддающуюся измерению оценку, например здесь: >> ...такая объективная причина, как потеря наглядности изображения. У меня создалось ощущение, будто наглядность=трехмерность модели. Н.С. Кузнецов в статье "К вопросу о наглядности изображений" (Начерт.геом. и инж.графика: сборник науч.-метод.статей. Вып. 1. 1973) отмечает, что наглядность зависит "от жизненного опыта, профессии, возраста и т.д. познающего человека". Т.е. одна и та же модель может становиться более наглядной по мере приобретения опыта. >> Когда вместо трехмерного объекта обучающемуся на уровне зрительного восприятия предлагается двумерное изображение, это приводит к возникновению психологического барьера для восприятия Когда к нам обращаются на незнакомом языке, это, пожалуй, тоже "приводит к возникновению психологического барьера", и преодолевается "лишь путем запоминания в памяти через монотонное обучение". Следует ли человечеству отказаться от изучения иностранных языков? Несомненно, "современные компьютерные средства обеспечивают высокую наглядность при 3D-электронном моделировании объекта за счет создания трехмерных компьютерных моделей", но лишь по одной причине - изоморфности моделируемого пространства и пространства модели. Станет ли 3D-электронная модель нагляднее плоского графика функции y=f(x)? Станет ли нагляднее плоской блок-схемы? Станет ли 3D-электронная модель четырехмерной фигуры нагляднее плоской модели четырехмерной фигуры? Опыт многомерного анализа данных убеждает нас в обратном. Я. Нильсен в книге о проектировании интерфейсов [Веб-Дизайн, 2003] отмечает, что «на практике следует отдавать предпочтение двумерной» графике, так как, в частности, «особое внимание управлению трехмерной моделью» мешает «выполнению основных задач». Только в 3D-конструировании основная задача "трехмерна". В остальных случаях анализ изображения человеком будет сопровождаться декодированием, которое тем проще, чем проще изображение. Таким образом, вывод о том, что "уход чертежа, как в его классическом, так и в электронном варианте исполнения из практической деятельности снимает задачу научить студентов составлению и чтению чертежа", делается на основе неверных посылок. Наконец, так ли уж "наглядна" трехмерная электронная модель сама по себе?
- стенки корпуса закрывают всю внутреннюю начинку. Для того, чтобы заглянуть внутрь, необходимо снимать детали или рассекать изделие, притом какая-нибудь часть все равно будет чем-нибудь закрыта; ни один из элементов не виден в натуральную величину, если только не активировать какой-нибудь ортогональный вид. На чертеже все виды, разрезы и сечения представлены одновременно. Что в этом случае называть "наглядностью"? Еще пара цитат Нильсена: "в результате эволюции зрение человека было адаптировано для передвижения по равнине, а не по деревьям", "абстрактные информационные пространства ... плохо поддаются реализации в виде трехмерных моделей", так, если пространство имеет "100 измерений, его трехмерная визуализация означает отбрасывание 97 измерений вместо 98" (для плоской); трехмерный интерфейс переносит недостатки объектов реального мира в компьютерную среду, задача которой - "сделать такие элементы лучше, чем в реальной жизни", так, человеку в реальном мире приходится переходить от объекта к объекту, огибать препятствия, перекладывать предметы, компьютерная система "позволяет мгновенно перемещаться к выбранному пункту назначения". Преимущества 3D-моделирования перед черчением не вызывают сомнения, но по причинам, как мне кажется, не имеющим отношения к наглядности, а именно: 1) простоте получения любого дополнительного изображения, 2) простоте внесения изменений, 3) возможности использования электронной модели на других этапах проектирования и подготовки производства. Именно это подтверждает справедливость вашего замечания об "уходе чертежа из современной практической деятельности", а не недостатки чертежа как такового. Наконец, "определяющим достоинством классического чертежа" стала, пожалуй, не его обратимость сама по себе (обратима и аксонометрия, и сопряженные центрально-ортогональные проекции), но обратимость + возможность решения прикладных задач (не только в машиностроении), компенсирующая недостаток "наглядности" простотой применения формальных методов. Фактически, решить задачу начертательной геометрии может любой студент независимо от его пространственного воображения, если усвоит алгоритмы. Многомерное моделирование вступает в ту область, где человеческий опыт (пространственное воображение) уже ничем не может помочь, на передний план выступают именно формальные методы. В этом отношении "классический чертеж" вовсе не потерял своих достоинств. Я так подробно остановился на этом, потому что в п.1 программы вы указываете - "Предмет, назначение, наглядность". Теперь, собственно, о наглядной геометрии. Цель и задачи книги Гильберта и Кон-Фоссена состояли в том, чтобы, отказавшись от чрезмерных (абстрактных) аналитических выкладок, представить в образной форме "грандиозные систематические построения алгебраической геометрии, римановой геометрии и топологии". В чем цель и задачи предлагаемого курса, а вернее той части, которая называется "наглядной инженерной геометрией", "наглядной многомерной геометрией"? Термин "инженерная геометрия" (прикладная геометрия) появился в 60-х гг и объединил начертательную геометрию, номографию, графические и графоаналитические методы, инженерное черчение (Четверухин Н.Ф. Прикладная геометрия и некоторые вопросы ее развития // Прикладная геометрия и инженерная графика. Вып. VIII. 1969). Термин "многомерная геометрия" довольно широк, но, как часть прикладной геометрии, многомерная геометрия включает "теорию обратимых чертежей n-мерного пространства", "частные виды обратимых чертежей", "многомерную аксонометрию", "НГ многомерных неевклидовых пространств", "геометрические методы исследования многокомпонентных систем" (Труды Моск.науч.-метод. семинара по НГ и ИГ. Выпуск 3. Труды МАИ. Выпуск 242. 1972). Содержание паспорта специальности 05.01.01 "Инженерная геометрия и компьютерная графика" приведено в докладе С.И. Роткова, в частности, многомерная геометрия тесно связана с номографией. Предлагаемый курс состоит из двух плохо связанных между собой частей - многомерной геометрии, которую вы собираетесь иллюстрировать на примере трехмерных моделей, и, собственно, трехмерного геометрического моделирования. В первой же части упоминаются "координатная система и преобразования координат и пространства", которые, очевидно, относятся к аналитической (т.е. не наглядной) области геометрии. Уточнение "Многогранники в n-мерной геометрии. Наглядно – геометрический подход" не помогает, поскольку ни в статье [1], ни в докладе нет ни одного наглядного представления многомерного многогранника. В целом, у меня создалось впечатление, что эта часть курса соответствует книге С.М. Куликова "Введение в начертательную геометрию многомерных пространств". Осталось не вполне ясным, как 3D-электронные модели помогут студентам в многомерном моделировании. Вы основываетесь на предположении, будто "взгляды на абстрактный многомерный мир ... доступны к восприятию наглядным способом изложения с проверкой основных постулатов через частные реализации на компьютерных моделях трехмерного пространства". Следуя методу индукции, можно было бы сказать и так: доступны с проверкой основных постулатов через частные реализации на моделях двухмерного или даже одномерного пространства, однако, это не работает: пересечение прямой с треугольником на плоскости, несмотря на "обобщение законов", осуществляется иначе, чем пересечение плоскости с тетраэдром в пространстве. В разделе "Поверхности. Обзор некоторых видов поверхностей...", судя по всему, планируется отказаться от практического построения линейчатых поверхностей общего вида (эллиптического гиперболоида, поверхностей Каталана, коноидов и др.), моделирование которых требует трудоемкого построения каркаса. Также вызывает вопрос содержание разделов "Позиционные задачи..." и "Метрические задачи..." в отношении "элементов пространства n измерений". В комментарии вы отметили, что "это уже математика (иллюстрации даются в виде рисунков)". В целом, мне кажется, еще требуют уточнения цели и задачи курса, понятие "наглядности", понятие инженерной геометрии, связь наглядности и многомерной геометрии. Клубок понятий, терминов и технологий в настоящее время мешает увидеть новую дисциплину, как нечто целое. Со стороны человека "в теме" видится что-то лоскутное. С уважением и наилучшими пожеланиями, Бойков |
|
ОГИБАЮЩАЯ СЕМЕЙСТВА ЛИНИЙ, Гирш Антон Георгиевич (29 февраля 2016 г. 22:43) |
Здравствуйте, Антон Георгиевич! Очень понравился ваш доклад, захотелось сразу на чем-нибудь попробовать. Интересно и для преподавателя, и для того, чтобы дать научную работу студенту. Спасибо! |
|
ИНЖЕНЕРНО-ГРАФИЧЕСКАЯ ПОДГОТОВКА СТУДЕНТОВ ТЕХНИЧЕСКОГО ВУЗА, Каменских Лариса Валентиновна, Мелкозёрова Людмила Яновна, Мошнинова Галина Николаевна (29 февраля 2016 г. 14:47) |
Уважаемый Дмитрий Евгеньевич, спасибо на добром слове! Уважаемая Марина Аркадьевна! Благодарю за обстоятельный и интересный комментарий. Ваш пример с профилем крыла очень нагляден, и мне очень захотелось поковырять связку MathCAD+Creo. Вы совершенно правы в том, что касается ситуации "как есть". Но в моих высказываниях я и не пытался противопоставить "циркули-линейки" вычислительным возможностям современных систем. Если уж говорить начистоту - все то, что мы вынуждены читать в курсе начертательной геометрии на первом курсе Высшей школы, уже давно должно бы перекочевать в школьную программу. И все-таки несколько замечаний:
- может быть, дело в индивидуальном восприятии (я - кинестетик), но мне такая форма геометрического моделирования некомфортна, хотя сам я постоянно имею дело с аналитическими выкладками: я не понимаю, что скрывается за циферками 0,2969 -0,1260 -0,3516 и др. Что изменится, если, к примеру, -0,3516 превратится в -0,3517. Может быть, специалисты в области самолетостроения видят за этими цифрами элементы конструкции ("I don't even see the code" (c) Matrix), что касается меня, я не могу сказать, чем эллипс 16y2+x2+48y+36−4x=0 отличается от эллипса 52x2+72xy+73y2−280x−290y+325=0, кроме того, что второй повернут. Аналитический и синтетический подходы дополняют друг друга, а вы делаете упор на аналитику ("Аналитика – абсолютная"). Ну и "гипербола". Конечно, мне известно, что кривая Безье позволяет моделировать любую конику (правда, кажется, не во всех еще школах проходят кривые Безье). Знаю, например, как в Компасе построить параболу, если задать ее вершиной и парой симметричных точек. Дело тут в другом. Во-первых, всякий инструмент CAD-системы является "черным ящиком". Во-вторых, всякая фигура может задаваться различными способами, а не только уравнением или системой уравнений. Например, экономный способ задать гиперболу - указать центр, вершину и любую точку (три точки); достаточный - указать пять точек кривой. Почему я должен, решая задачу, брать координаты точек (с округлением?), решать задачу аналитически ("как в тетрадке"), чтобы угодить инструментам системы? Одно из правил хороших интерфейсов: пользователь должен решать задачу, а не придумывать, как совладать с рычагами и кнопками. Гипербола в данном случае была примером очень простой линии, которую до сих пор полноценно использовать невозможно. В частности, "чем плох тот метод"? - тем, что построенная таким способом кривая не может использоваться в наложении параметрических связей - в построении касательных и нормалей (инструменты CAD-системы, как оказалось, могут работать только с "родными" линиями). Ну и "интерфейсная" причина: почему я должен придумывать параметры конуса и расположение плоскости, подходящих для ее построения, когда знаю, что достаточно указать три точки. Поэтому, возвращаясь к кривой (1), точки которой, вероятно, можно свести к какой-либо серии построений на основе библиотеки встроенных кривых (среди них не обязаны быть только окружности и эллипсы). Так вот, хорошая геометрическая система, в моем понимании, должна дать мне возможность, выполнив один раз эту серию построений вручную, повторить ее произвольное число раз автоматически для достижения необходимой точности; поменять входные точки и линии, и опять повторить. Такой подход открывает возможности не только к использованию готовых кривых "Airfoil Nasa 1432-01", но и к автоматизации конструирования новых. Есть ли в этом какое-то противоречие с парадигмой "автоматизированных технологий"? Что касается "парадигмы", тут нужно много и основательно думать. Я не считаю себя в праве и вполне компетентным. Автоматизация влияет не только на начертательную геометрию, - на высшую математику, электротехнику и пр. влияет не меньше. Нужно ли изучать интегралы, матрицы, векторы, вручную решать ДУ, если современные компьютерные системы делают это лучше и быстрее? Зачем нужны "тетрадки", если есть MathCAD и Mapple? И да, я за сотрудничество. с уважением, Бойков |
|
ИНЖЕНЕРНО-ГРАФИЧЕСКАЯ ПОДГОТОВКА СТУДЕНТОВ ТЕХНИЧЕСКОГО ВУЗА, Каменских Лариса Валентиновна, Мелкозёрова Людмила Яновна, Мошнинова Галина Николаевна (28 февраля 2016 г. 14:47) |
Уважаемая Марина Аркадьевна, с автоматизированными технологиями складывается любопытная ситуация. С одной стороны, современные САПР настолько хороши, что все крики о "плоских чертежах" и "начертательной геометрии" кажутся консервативными криками из эпохи карандаша и кульмана. С другой стороны, мне кажется, мы уже увидели потолок современных автоматизированных геометрических систем - все они ("лучше, больше, выше") реализуют едва ли не один и тот же набор инструментов моделирования (к сожалению, я не достаточно знаком с технологией "Непосредственного редактривания" в новом Solid Edge): параболоиды, гиперболоиды, каталана и др., хорошо исследованные, приходится создавать приближенно на основе Безье и NURBS. Вплоть до ручного рисования достаточного числа линий каркаса. Какая уж тут автоматизация, если даже гиперболу построить нельзя, иначе как рассечением конуса. В таких условиях уже крики о более широком внедрении CAD-систем ("лучше, больше, выше") в учебный процесс выглядят консервативными (зачем нужны атомные станции, если новенькие угольные ТЭЦ так хороши?) Очевидно, мы стоим перед противоречием, требующим творческого (ТРИЗ?) решения. Начертательная геометрия прошлого века с ее многомерными пространствами, нелинейными преобразованиями, конструктивными алгоритмами построения кривых и поверхностей содержит богатую основу для развития инструментария геометрических систем. Я полагаю, "Симплекс" Д.В. Волошинова - только первая ласточка. Зато студенты забыли последнюю геометрию, какую знали, и могут лишь то, что могут их CAD-редакторы. с уважением, Бойков |
|
К РЕШЕНИЮ ЗАДАЧИ О ТОЧКАХ ПЕРЕСЕЧЕНИЯ КРИВЫХ ВТОРОГО ПОРЯДКА, Волошинов Денис Вячеславович (28 февраля 2016 г. 1:38) |
Здравствуйте, Денис Вячеславович! Большое спасибо за доклад. Как вы верно отметили, "в литературе и в Сети практически нет материалов" по этому и другим, близким вопросам, и все приходится выводить заново, изобретать велосипед. Не встречались ли вам аналитические выкладки к построению коник, касательных к коникам? Прямых, касательных к парам коник? Будет очень хорошо, помимо прочего, дополнить методические материалы конференции публикациями, освещающими во всей полноте те или иные сугубо прикладные вопросы геометрического моделирования: полезно для студентов, занимающихся научной работой, для преподавателей и аспирантов, разрабатывающих технические средства преподавания. Очень рад услышать, что в "Геометрии и графике" будут выходить статьи по Симплексу. Отличная новость! с уважением, Бойков |
|
ЭЛЕМЕНТЫ ТРИЗ В ЛЕКЦИЯХ ПО НАЧЕРТАТЕЛЬНОЙ ГЕОМЕТРИИ, Ракитская Мария Валентиновна (27 февраля 2016 г. 17:47) |
Комментарий удален, т.к. нарушает структуру страницы "Последнее", где он дублируется. Ширина рисунка в коменнтариях не должна превышать 500 точек растра! Для обмена более обширной информацией можно воспользоваться разделом "В кулуарах". С уважением к участникам, Администрация |
|
ЭЛЕМЕНТЫ ТРИЗ В ЛЕКЦИЯХ ПО НАЧЕРТАТЕЛЬНОЙ ГЕОМЕТРИИ, Ракитская Мария Валентиновна (27 февраля 2016 г. 12:49) |
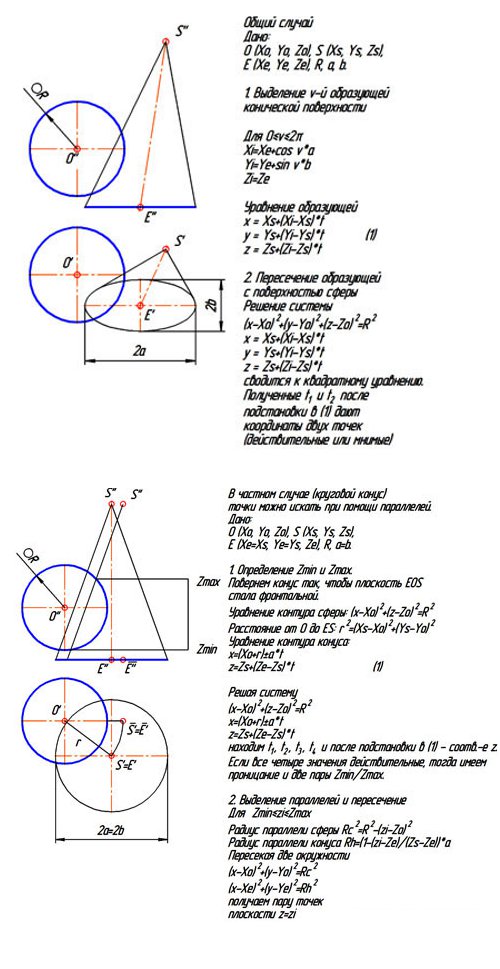
Уважаемая Мария Валентиновна, тогда ваш случай легко сводится к моему случаю 1. Один, максимум два поворота системы коодинат (аффинная матрица M). Очередная точка траектории - координаты Sx, Sy, Sz. Остается найти эллиптическое сечение в какой-то горизонтальной (фронтальной/профильной) плоскости (на основе положения центра и угла при вершине конуса) - величины Ex, Ey, Ez и a, b. Рассчитать точки кривой пересечения. Повернуть точки обратно (матрица M^-1). у уважением, Бойков |
|
ГЕОМЕТРИЧЕСКАЯ ПОДГОТОВКА БАКАЛАВРОВ В УСЛОВИЯХ УХОДА КЛАССИЧЕСКОГО ЧЕРТЕЖА ИЗ СОВРЕМЕННОГО ВЫСОКОТЕХНОЛОГИЧНОГО ПРОИЗВОДСТВА, Соколова Людмила Сергеевна (26 февраля 2016 г. 22:07) |
Уважаемая Людмила Сергеевна! Спасибо за любопытный доклад, к большому моему сожалению не имею под рукой статьи [1]. До сих пор я предполагал, что именно многомерные фигуры и связи проще анализировать (не представлять, представить трехмерному человеку четыре измерения принципиально невозможно) плоские изображения. Отсюда популярность таблиц и графиков, и разных способов снижения размерности (проецирования?!) в многомерном анализе. Подскажите, как наглядно, не пользуясь ортогональными проекциями, изобразить две пересекающиеся комплексные прямые вида A(x+jx')+B(y+jy')+C=0 в пространстве (x, x', y, y')? |
|
ИНЖЕНЕРНО-ГРАФИЧЕСКАЯ ПОДГОТОВКА СТУДЕНТОВ ТЕХНИЧЕСКОГО ВУЗА, Каменских Лариса Валентиновна, Мелкозёрова Людмила Яновна, Мошнинова Галина Николаевна (26 февраля 2016 г. 19:02) |
Уважаемый Дмитрий Евгеньевич, мне нечего возразить. Все это верно. Но, опасаюсь, при такой строгости мы на моем теплоэнергетическом факультете рискуем вовсе отказаться от деталирования: наши трубопроводы, краны и вентили состоят сплошь из "стандартных" деталей и "заимствованных" изделий. |
|
ЭЛЕМЕНТЫ ТРИЗ В ЛЕКЦИЯХ ПО НАЧЕРТАТЕЛЬНОЙ ГЕОМЕТРИИ, Ракитская Мария Валентиновна (26 февраля 2016 г. 18:57) |
Уважаемый, Михаил Николаевич, бесспорно, ТРИЗ хорош для поиска "озарения", необходимого в решении творческой задачи; но, касаясь НГ и ИГ, я не вижу, где методы ТРИЗ могли бы помочь в решении задачи без знания геометрии. Наши студенты зачастую просто не знают геометрии, они умудряются получать весьма оригинальные решения, но не способны проверить, правильные эти решения или нет. Скажем так, если я увижу, как студент, сознательно применяя методы ТРИЗ (увеличение, уменьшение, наоборот, дробление, соединение, разделение в пространстве и времени, Х-элемент и др.), решит задачу олимпиадного уровня (вот уж где простор для творчества), я сразу и полностью поменяю свое мнение. Пока же я опасаюсь увлечься изучением ТРИЗ на примере некоторых задач НГ, вместо изучения самой НГ. с уважением, Бойков |
|
ИНЖЕНЕРНО-ГРАФИЧЕСКАЯ ПОДГОТОВКА СТУДЕНТОВ ТЕХНИЧЕСКОГО ВУЗА, Каменских Лариса Валентиновна, Мелкозёрова Людмила Яновна, Мошнинова Галина Николаевна (26 февраля 2016 г. 17:10) |
Уважаемая Марина Аркадьевна, если я вас правильно понял, вы имеете в виду учить студентов, используя построения сразу трехмерной модели? Почему же нельзя? Очень даже можно, но это совершенно не соответствует основному методу начертательной геометрии, которая в качестве инструмента моделирования использует изображения (проекции). То есть используя инструменты CAD-системы мы можем учить трехмерному моделированию при помощи трехмерных инструментов. Набор этих инструментов всегда ограничен (хотя и достаточен для решения прикладных задач). Начертательная геометрия дает, в принципе, способ трех, четырех и более -мерного моделирования. Этот способ не ограничен, скажем, операциями выдавливания/вращения/лофтинга и кривыми/поверхостями Безье и NURBS; здесь можно строить любые кривые и оболочки. Инструментом моделирования являются изображения. Но автоматизированной системы для подобного моделирования нет, кроме "Симплекса" Д.В. Волошинова и, скажем, языков программирования. Такому моделированию при помощи стандартных инструментов Компаса и Автокада научить невозможно. Наоборот, многие приемы становятся бессмысленными (прямые уровня для построения перпендикуляра, вспомогательные плоскости и поверхности-посредники и др.), да и сами "классические задачи" теряют смысл, спрятанные за кнопочками. Промежуточное решение - учить студентов строить чертежи трехмерых деталей и сборок в CAD-системах - Алексей Алексеевич назвал "профессией чертежника электронной модели". В нецелесообразности этого я и сам убежден: построенная таким способом электронная модель неприменима (пока невозможна полоценная конвертация электронных проекций и сечений в 3d), и требует неоправданно лишних усилий при создании. |
|
ЭЛЕМЕНТЫ ТРИЗ В ЛЕКЦИЯХ ПО НАЧЕРТАТЕЛЬНОЙ ГЕОМЕТРИИ, Ракитская Мария Валентиновна (26 февраля 2016 г. 16:00) |
Здравствуйте, Мария Валентиновна! Спасибо за интересный доклад, я сам нокоторое время присматривался к ТРИЗ, читал работы Альтшуллера и его учеников и даже подумывал включать те или иные элементы в учебный процесс, но все-таки пришел к выводу, что ТРИЗ слабо формализуема (что конкретно в той или иной задаче считать Х-элементом? почему в одной задаче это точка, в другой - прямая, в третьей плоскость?). В частности, глядя на примеры в докладе у меня создалось впечатление, что методы ТРИЗ и решения некоторых предложенных задач, что называется, "притянуты" (например, "подушка" - плоскость развертки?). Многие предложенные задачи легко решаются через применение формальных геометрических процедур, в частности, с опорой на понятие "геометрического места", - метод, хорошо зарекомендовавший себя в геометрии. Причем, дают гарантированный результат. С другой стороны ТРИЗ - это целый комплекс методов, заслуживающий отдельного цикла лекций и практических занятий, и тут мы уже рискуем перетянуть одеяло с начертательной геометрии. А оно и так короткое. В общем, задумка интересная, и от себя хочу пожелать вам успехов, буду наблюдать с предельным вниманием. Если позволите, я также попробую ответить на вопрос, заданный вами в комментариях к докладу Антона Гергиевича. Для нахождения произвольного числа общих точек конуса и сферы можно воспользоваться следующими соотношениями:
Во втором случае имеем аналитическую реализацию традиционного алгоритма НГ со вспомогательными секущими плоскостями. В обоих алгоритмах найденные координаты пар точек следует сохранять в разные массивы (разделяя на верхнюю-нижнюю или ближнюю-дальнюю). Ни тот, ни другой алгоритм, впрочем, не находят контурных точек (1 рода), для чего в общем случае пришлось бы пересекать пару коник (см. доклад Д.В. Волошинова), и не реализуют проверку видимости. Литература, которая может быть полезна студентам: Точки, прямые, плоскости, преобразования: 1. Ананов Г.Д. Графоаналитическая геометрия. Л.: ЛИСИ, 1975. 116 с. http://f.webtute.ru/indexcol.php?id=5&m= Программирование в преподавании НГ: 2. Михайленко В.Е. Применение ЭВМ в преподавании курса начертательной геометрии / В.Е. Михайленко, В.А. Анпилогова, Н.И. Седлецкая. Киев: КИСИ, 1979. 68 с. http://f.webtute.ru/indexcol.php?id=11&m= 3. Курс начертательной геометрии на базе ЭВМ / А.М. Тевлин, Г.С. Иванов, Л.Г. Нартова и др. М.: Высшая школа, 1983. 176с. с уважением, Бойков |
|
ИНЖЕНЕРНО-ГРАФИЧЕСКАЯ ПОДГОТОВКА СТУДЕНТОВ ТЕХНИЧЕСКОГО ВУЗА, Каменских Лариса Валентиновна, Мелкозёрова Людмила Яновна, Мошнинова Галина Николаевна (24 февраля 2016 г. 22:53) |
Здравствуйте, уважаемые коллеги. Прошу прощения за молчание. Уважаемый Дмитрий Евгеньевич, никоим образом не хочу ставить под сомнение справедливость ваших замечаний, просто хотелось разделить, как водится, мух и котлеты. О котлетах. У нас в институте альбом Аксарина используется, в частности, на теплоэнергетическом факультете, хотя ошибки в нем есть. Все ошибки оригинальных заданий мы со студентами обговариваем. Иногда бывает эффективно показать ошибку и сказать, что так делать нельзя. В представленном чертеже стандартная деталь Маховичок, насколько я могу судить, включена в раздел Детали для того, чтобы ее можно было деталировать. Отсюда и все лишние изображения. Плохо или нет, что студентов общетехнической специальности учат деталированию на примере подобной детали? Не знаю. Впоследствии мои студенты чертят только при проектировании редуктора, а дальше - предметные САПР и схемы. Очевидно, для конструкторов подобные задания неприемлемы. О мухах. Ошибок в представленном коллегами чертеже много. Это и чисто геометрические, и оформления, и владения графическим пакетом (пересечение центровых линий на виде Б было бы правильным при использовании инструмента "Обозначеие центра") и др. Очевидно, чертежи, иллюстрирующие доклад на конференции, должны тщательно проверяться. Но, также очевидно, что после первых откликов докладчики сделали выводы. Уважаемый Николай Андреевич, рад новой, пусть заочной, встрече! Прошу прощения, что не упел ответить. Алексей Алексеевич, на мой взгляд, дал исчерпывающий ответ на ваш вопрос. Уважаемый Алексей Алексевич, рад новой встрече! Хочу немного пояснить свое короткое и потому сумбурное замечание насчет "очередности". Возникновение перечисленных геометрических ошибок является следствием, конечно же, неумения работать с проекциями и отсутствия пространственного воображения, которое, как всем нам хорошо известно, у современных первокурсников ужасное. Они не понимают, откуда берутся линии на чертеже, и не способны самостоятельно проверять свои чертежи. В таких условиях трехмерная модель может стать "костылем", способом "верификации" (об этом будет моя статья на этой конференции), подспорьем к проверке ошибок, тем более, что практическая работа студентов, по словам докладчиков, как раз и завершается созданием трехмерной модели. Сам часто использую трехмерные модели в Компасе в качестве наглядных пособий на семинарах, поскольку инструмент переключения вида (спереди -> сверху -> спереди -> слева) позволяет, не отрываясь от динамического наглядного изображения, быстро получать ортогональные виды и обсуждать их особенности. Насчет разговора. Вот в этой фразе кроется ответ "вполне можно сделать эскиз модели в глазомерных пропорциях". Для того, чтобы сделать эскиз, студент должен уметь его делать. Если вы имеете в виду аксонометрическое изображение (технический рисунок), тогда отметим, что построить его сложнее, чем эскиз в двух-трех видах, в частности, с использованием кривых поверхностей - сфер, торов. Эскиз (тот же чертеж) - 1) самый компактный и быстрый способ фиксации сведений для последующего моделирования, 2) самая доступная форма геометрического моделирования, требующая лишь листа в клетку и карандаша. Совокупность линий содержит по определению меньше информации, чем реалистичное фотографическое изображение. Чертеж - это конспект реалистичной модели. Я убежден, что фотореализм нужен только в дизайне, в остальных случаях - оправдано именно сжатие информации. Например, 3d наглядно, пока все нюансы формы видимы и хорошо различимы, а как поступать со сложными пазами, вырезами и отверстиями? Насколько сохраняет свое удобство моделирование таких пазов в 3d? Сколько придется рассекать трехмерную модель, чтобы все их увидеть, и как долго придется ее вертеть, чтобы все это уяснить? >> мы учим студентов копировать, а не разрабатывать что-то новое. На первом курсе мы учим их основам геометрического моделирования, разве не так? Можем ли мы научить человека писать, не научив предварительно читать? Я полагаю, на первом курсе наша задача весьма скромна - дать базу для последующей проектной деятельности. Базу геометрического моделирования составляют: 1) знание геометрических фигур (3d здесь, вероятно, нагляднее, но вообще-то это задача школы), 2) знание способов формообразования (здесь 3d, наверное, тоже имеет преимущества, но есть пара "но", о которых далее), 3) знание геометрии (никакое развитое воображение не поможет решить задачу Пеклича о построении прямой, пересекающей четыре другие, попарно скрещивающиеся, если, конечно, редактор не содержит соответствующей "кнопки"), а геометро-логическое мышление легче тренировать в 2d (например, сравнить три плоских поворота и один трехмерный поворот фигуры; параллельность прямой и плоскости; перпендикулярность пары прямых; нормальность и касательность к поверхностям), 4) те самые "но": поскольку плоское изображение - фундаментальный инструмент анализа и исследования пространства (фото- и киносъемка, например), необходимо уметь им пользоваться, т.е. логично исследовать геометрические фигуры (1) и принципы формообразования (2) посредством изображений. Метод двух изображений (не обязательно чертеж Монжа) есть один из наиболее общих приемов обратимого моделирования пространственной геометрии; но из всех прочих - пары центральных проекций, центрально-ортогональные сопряженные проекции - именно ортогональный чертеж проще всего. Можно, к примеру, на первом курсе моделировать геометрию, пользуясь сразу парой центральных проекций. Но стоит ли? >> Учим профессии чертежника электронной модели, а она никому не нужна. А вот здесь я согласен. Сегодня есть необходимость в некотором количестве плоских моделей, например, схем. Трех- и более мерное теоретическое моделирование (задачи НГ) вполне можно реализовывать инструментами плоских редакторов, имеющих точность, более высокую, чем лист и карандаш. Однако, чертить электронные модели деталей и сборок тем способом, как это предоставляют Компас и AutoCAD (например, у нас даже имелись бы средства для автоконвертации в 3d), считаю крайне неудачным вариантом, поскольку ни Компас, ни AutoCAD не приспособлены для моделирования пространства при помощи изображений. Даже в TFlex необходимо долго складывать проекции, переносить в пространство, и там, фактически, заново воссоздавать трехмерные формы. Но это не означает, что невозможна геометрическая система, полноценно управляющая пространством при помощи изображений. Тем более такая система будет полезна там, где необходимо совмещать 2d (моделирование кривых и оболочек мгновенными преобразованиями или пересечениями многообразий) и 3d (традиционные конструктивные операции). с уважением, Бойков |
|
ИНЖЕНЕРНО-ГРАФИЧЕСКАЯ ПОДГОТОВКА СТУДЕНТОВ ТЕХНИЧЕСКОГО ВУЗА, Каменских Лариса Валентиновна, Мелкозёрова Людмила Яновна, Мошнинова Галина Николаевна (21 февраля 2016 г. 20:43) |
Уважаемые коллеги, мне кажется, для ясности необходимо представить задание (с. 33-34) альбома Аксарина П.Е. (1993), которым обеспечены графические кафедры многих вузов (нашего, в том числе), и некоторые справедливые вне такого контекста вопросы решатся сами собой. Скажем так, это - тот методический материал, с которым приходится работать.
Со своей стороны отмечу, однако, что выполнение сборочного чертежа до моделирования сборки в данном случае привело к появлению ряда геометрических ошибок (фаски на шестигранниках, отсутствие линии на виде слева, наружная резьба на штуцере и втулке на главном виде и внутренняя - на виде слева), которые станут очевидны, если сравнить "ручной" чертеж (в Компасе или на формате) и ассоциативный. Поэтому в качестве самопроверки студентам можно порекомендовать их сравнивать. |


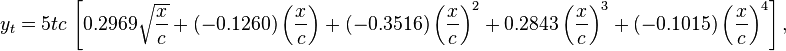 (1)
(1)