БАЗОВЫЕ АЛГОРИТМЫ КОМПЬЮТЕРНОЙ ГРАФИКИ (что там, за “кнопками”?)

Приведен обзор базовых алгоритмов компьютерной графики, изучаемых будущими специалистами в области программирования графических систем.

Компьютерные технологии так стремительно видоизменили рабочее место и инструмент проектировщика и конструктора, что остается лишь констатировать и повсеместно учитывать этот факт. Они не просто обеспечивают более высокую эффективность проектно-конструкторской работы, но и утвердили принципиально новые возможности. В первую очередь, – это работа с естественным для человека трехмерным пространством (непосредственно с геометрической 3D-моделью, а, не с ее проекциями) и обеспечение в процессе конструирования информационной поддержки всего жизненного цикла изделия. Кроме того, достигнут качественно новый уровень визуализации конструкторской документации: технология WYSIWYG, презентационная графика, аудиовизуальные документы и многое другое. Мало того, возможности «нового» конструкторского инструмента стандартами ЕСКД возведены в ранг требований.

Но, вместе с этим, объяснима и обеспокоенность относительно подконтрольности этого инструмента пользователю, учитывая, что работа программ не «видна» так, как мы привыкли при ручных геометрических построениях карандашом с линейкой и циркулем. Естественно желание найти компактные обобщения и представления теоретической основы программных «технологий» и «теории» компьютерной лексики для описания традиционного языка техники – чертежа. В этой же плоскости находится проблематика оптимального сочетания методов и положений «традиционных» технологий инженерной графики и «современных» информационных технологий, ставя задачу оптимизации образовательных программ и межпредметных связей.

Представляется, что именно с этих позиций будет интересен обзор образовательного пространства будущих специалистов в области программирования графических систем, как занимающихся тем, “что за кнопками” в программах подготовки “наших” студентов. Для этого обратимся к базовым алгоритмам компьютерной графики, которые рассматриваются в дисциплине “Компьютерная геометрия и геометрическое моделирование” одной из таких образовательных программ.

В частности согласно ФГОС-3 дисциплина “Компьютерная геометрия и геометрическое моделирование” относится к базовой части профессионального цикла по направлению подготовки 010200.62 – Математика и компьютерные науки. Вместе с дисциплинами «Аналитическая геометрия» и «Дифференциальная геометрия и топология» участвует в формировании одних и тех же компетенций будущих бакалавров. С учетом совсем молодого по историческим меркам возраста компьютерной геометрии и графики ограничим информационную базу широко известными учебными изданиями, прошедшими апробацию в учебном процессе высших технических учебных заведений на протяжении одного-полутора десятка лет [1, 2, 3]. Обзор будет, конечно, неполным, в силу динамического развития и постоянного совершенствования, обновления и пополнения содержания предмета обзора, к тому же опирающегося на учебную литературу, прошедшую этап включения в учебные программы и апробацию, что требует дополнительного времени.

1. Виды компьютерной графики и способы визуализации

Выделяют три вида компьютерной графики: растровую, векторную и фрактальную. В растровой графике основным элементом изображения является пи́ксель (англ. pixel – наименьший логический элемент двумерного цифрового изображения, или элемент матрицы дисплеев, формирующих изображение), в векторной – линия (прямая или кривая). Во фрактальной геометрии (от лат. fractus, «сломанный, разбитый») – это бесконечно самоподобная геометрическая фигура, каждый фрагмент которой повторяется при уменьшении масштаба. Также в отдельный, четвертый, вид графики часто выделяют и 3D- или трёхмерную графику. «От двухмерной она отличается тем, что подразумевает построение проекции трехмерной модели сцены (виртуального пространства) на плоскость» [4].

Наряду с видом графики различают способ визуализации. Наиболее известны также как и виды компьютерной графики, два способа визуализации: растровый и векторный. Первый используется в таких графических устройствах, как дисплей, телевизор, принтер; второй – в векторных дисплеях, плоттерах, каттерах. Чаще способ визуализации не совпадает с видом графики, для их совмещения требуется конвертация, их вообще надо различать. В частности смешение геометрического моделирования с процессом вывода изображения на экран может привести к выводу о тождественности геометрической модели и ее аксонометрической проекции, или о том, что в основе трехмерной графики лежит метод проецирования.

Программы САПР относятся к программам векторной графики, т.е. оперируют с линиями. Теоретической основой геометрического моделирования являются дифференциальная и аналитическая геометрии, вариационное исчисление, топология и разделы вычислительной математики, численные методы, теория В-сплайнов, методы моделирования различных кривых, поверхностей и тел, а также алгоритмы выполнения операций над ними и вычисления их геометрических характеристик, установления вариационных зависимостей параметров геометрических объектов. Геометрическое моделирование изучает методы построения кривых линий, поверхностей и твердых тел, методы выполнения над ними различных операций и методы управления численными моделями [5].

2. Координатный метод в компьютерной графике

Без преувеличения координатный метод можно охарактеризовать как основной метод компьютерной графики. В координатах задают положение и форму всех геометрических объектов и выполняют их преобразования. В компьютерной графике задействованы все известные из аналитической геометрии координаты – всевозможные прямолинейные и криволинейные, предусмотрены самые широкие возможности по использованию координат.

Привычный аппарат декартовых координат, не подходит для решения некоторых важных задач в силу следующих соображений:

а) в декартовых координатах невозможно описать бесконечно удаленную точку. А многие математические и геометрические концепции значительно упрощаются, если в них используется понятие бесконечности;

б) с точки зрения алгебраических операций, декартовы координаты не позволяют провести различия межу точками и векторами в пространстве;

в) невозможно использовать унифицированный механизм работы с матрицами для выражения преобразований точек;

г) декартовы координаты не позволяют использовать матричную запись для задания перспективного преобразования (проекции) точек.

Для решения этих проблем используются однородные координаты (введены Плюккером в качестве аналитического подхода к принципу двойственности Жергонна-Понселе). Однородные координаты – мощный математический инструмент, связанный с определением положения точек в пространстве и находящий свое применение в различных разделах компьютерной графики – геометрическом моделировании, визуализации, машинном зрении и т.д. Однородные координаты явно или неявно используются в любом графическом пакете [6].

У однородных координат на плоскости есть простая геометрическая интерпретация. Преобразование из однородных координат (x,y,z) в евклидовы (x/z,y/z,1) эквивалентно проекции точки на плоскость z=1 вдоль линии, соединяющей точку с началом координат.

К координатам может быть применено двумерное и трехмерное аффинное преобразование: повороты вокруг координатных осей, отражения относительно координатных плоскостей, перенос и композиция преобразований.

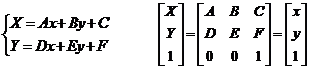
Общий вид аффинного преобразования на плоскости имеет вид:

где (x, y) – двумерная система координат, (X, Y) – координаты старой СК в новой системе координат, A, B, C, D, E, F – константы.

Важнейшей операцией при визуализации трехмерной графики является проектирование (мат.). Проектирование – это преобразование, ставящее в соответствие точкам трехмерного пространства точки на некоторой плоскости, называемой картинной.

В компьютерной графике используются два основных вида проектирования: параллельное и перспективное. Как произвольное аффинное преобразование, так и параллельное и перспективное проектирование могут быть записаны при помощи матриц однородных преобразований. Для сравнения приводим матрицы канонического уравнения параллельного проектирования, осуществляемого на плоскость Oxy вдоль оси Oz и канонического уравнения перспективного проектирования:

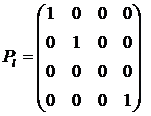
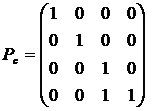
Обращает на себя внимание, насколько схожи в плане сути и трудоемкости вычисления для получения параллельной и перспективной проекций в программах компьютерной графики, настолько же не похожи, особенно по трудоемкости, построения при ручном построении.

3. Геометрические объекты

При описании геометрических объектов используются такие математические объекты и их свойства как прямые и плоскости, кривые линии, двухмерные кривые, поверхности, кривизна линий на поверхности, криволинейные координаты. Все эти вопросы всесторонне разработаны и подробно освещены в курсе аналитической геометрии. Можно говорить о том, что компьютерная графика в части описания геометрических объектов имеет в лице аналитической геометрии готовый к использованию математический аппарат. В компьютерной графике могут решаться системы линейных и нелинейных уравнений. Это позволяет определять точки пересечения линий, линии и поверхности, построение линий пересечения поверхностей и другие вычисления.

Одним из важнейших инструментов систем автоматизированного проектирования и программ компьютерной графики стали сплайны. Сплайн – гладкая кривая, которая проходит через две или более опорных точек, а также имеет расположенные вне ее управляющие точки, влияющие на форму сплайна. Наиболее общие типы сплайнов – кривые Безье и B-сплайны (B-spline curves). Типичным примером сплайнов являются также неоднородные рациональные B-сплайны (Non-Uniform Rational B-Spline – NURBS). Сплайны состоят из вершин (Vertices) и сегментов (Segments). Каждая вершина сплайна имеет касательные векторы (Tangents), снабженные на концах управляющими точками, или маркерами (Handels). Маркеры касательных векторов управляют кривизной сегментов сплайна при входе в вершину, которой принадлежат касательные векторы, и выходе из нее.

Кривые Безье были разработаны в 60-х годах XX века независимо друг от друга Пьером Безье из автомобилестроительной компании «Рено» и Полем де Кастельжо из компании «Ситроен», где применялись для проектирования кузовов автомобилей.

Кривые Безье описываются в параметрической форме:

x=P_x(t), y=Py(t).

Значение t выступает как параметр, которому отвечают координаты отдельной точки линии.

Многочлены Безье для Px и Py имеют следующий вид:

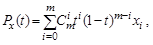
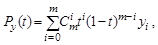
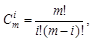
где C_mⁱ– сочетание m по i, а x_i, y_i – координаты точек ориентиров P_i. Значение m(1, 2, 3) можно рассматривать и как степень полинома, и как значение, которое на единицу меньше количества точек-ориентиров.

4. Методы построения поверхностей

Плоскостные (полигональные) модели, или полигональные сетки, находят в компьютерной графике самое широкое применение. Они представляют поверхности геометрических объектов в виде набора состыкованных друг с другом плоских полигонов. Традиционное для компьютерной графики описание полигональной модели объекта является иерархическим и включает список вершин, список ребер и список полигонов объекта. Контур полигона определяется вершинами, которые соединены отрезками прямых. В векторной форме полигон задается перечислением своих вершин: P={p₁, p₂, …, p_n, p₁}.
Основным недостатком полигональных моделей является необходимость в большом количестве полигонов для представления сложных, особенно криволинейных, поверхностей. Это означает, что при синтезе динамических изображений геометрические параметры нужно пересчитывать у большого числа примитивов в режиме реального времени. Поэтому наряду с плоскими поверхностями в графических системах применяются криволинейные примитивы, в частности, поверхности второго порядка
Часто отображаемые объекты, особенно природные, имеют довольно сложную форму, не допускающую универсального аналитического описания в целом. Их форма задается набором характерных (опорных) точек, принадлежащих поверхности объекта. Опорные точки получаются в результате замеров на реальных объектах, их сканирования с помощью 3D-сканеров или назначаются разработчиками. В качестве примера можно назвать составленную геодезистами карту высот участка земной поверхности. Самый простой подход – соединить опорные точки участками плоскости, то есть применить полигональную модель. Однако для достижения реалистичности отображения объекта его полигональная модель должна насчитывать тысячи и десятки тысяч полигонов, что повышает требования к объему памяти и производительности графической системы. Не приносит успеха и применение квадрик, так как в этом случае возникает проблема их гладкой стыковки в единую поверхность. Поверхности неаналитических форм представляют кусочно-полиномиальными функциями – сплайнами.
В геометрическом моделировании часто применяется бикубическая поверхность Безье. Ограничениями при построении этой поверхности является ее прохождение через угловые точки характеристического многогранника и заданные на его границах наклоны касательных. Кроме сплайнов Безье, в компьютерной графике широко применяются базовые сплайны, или В-сплайны («би-сплайны»).
Широкими изобразительными возможностями обладают рациональные бикубические сплайны. В компьютерной графике обычно применяют рациональные B-сплайны на неравномерной сетке (Non-Uniform Rational BSplines – NURBS). В их описание входят числовые параметры формы (весовые коэффициенты), позволяющие управлять формой поверхности [3].

Использование аналитических поверхностей позволяет существенно повысить эффективность и наглядность изучения свойств этих поверхностей, как в исследованиях, так и в учебном процессе [7, 8].

5. Многоугольники (полигоны)

C полигонами связано большое количество вычислений, в том числе тестов. Тесты могут не давать исчерпывающий ответ на поставленный вопрос, но могут ограничить область поиска и сократить время и машинные ресурсы. Например, человек, не задумываясь, ответит на следующие вопросы на основании того, что он видит. В компьютерной графике поиск ответов на эти вопросы формализован.
Свойства плоских многоугольников
Пересечение прямой линии с полигоном. Прямая пересекает полигон, если существует хотя бы одна пара вершин, лежащих от нее по разные стороны (это свойство предполагает сравнение для всех имеющихся пар вершин, а не только смежных).
Выпуклость полигона. У выпуклого полигона все углы при вершинах p_i-1, p_i , p_i+1 одного знака. Другими словами, при обходе выпуклого полигона по замкнутому контуру в произвольном направлении каждая вершина p_i+1 расположена относительно ребра p_i-1p_i одинаково для всех значений i: слева при положительном направлении обхода и справа при отрицательном.
Самопересечение полигона. Полигон является самопересекающейся замкнутой ломаной линией, если у него существует хотя бы одна пара пересекающихся отрезков. Два отрезка пересекаются друг с другом, если концы одного находятся по разные стороны от прямой другого и наоборот (тестироваться должны все пары несмежных ребер полигона)
Тесты ориентации точки относительно полигона
Ограничимся только перечислением: выпуклый тест, габаритный тест, угловой тест. Перечисленные тесты, будучи проведенными до начала вычислений, существенно сокращают время вычислений и вообще оптимизируют работу компьютера.

6. Базовые растровые алгоритмы

Алгоритмы вывода прямой

Растровые алгоритмы используется для рисования линий на экране компьютера. Изображение отрезка на экране должно отвечать некоторым минимальным требованиям:

- концы отрезка должны находиться в заданных точках;

- отрезки должны выглядеть прямыми,

- яркость вдоль отрезка должна быть постоянной и не зависеть от длины и наклона.

В силу дискретности ни одно из этих условий не может быть точно выполнено на растровом дисплее [9].

Растровые алгоритмы построения прямой призваны получить максимально возможное приближение к этим требованиям при минимальных ресурсах.

Прямое вычисление координат. Пусть заданы координаты конечных точек отрезка (x₁,y₁) и (x₂,y₂). Координаты внутренней точки отрезка вычисляются следующим образом: y=F(x): y=y₁+(x-x₁)(y₂-y₁)/(x₂-x₁).

Для того чтобы свести к минимуму вычисления в цикле, все операции над константами выносятся из тела цикла: k=(y₂-y₁)/(x₂-x₁), yy=y₁-x₁*k.

В цикле вычисляется y=yy+x*k.

С учетом того, что вычисление дробей происходит с определенной погрешностью, возможна ситуация, когда на последнем шаге цикла x окажется не равным x2.

В 1962 году сотрудник компании IBM Джек Е. Брезенхэм (Jack E. Bresenham) предложил подход, позволяющий разрабатывать так называемые инкрементные алгоритмы растеризации. Алгоритм Брезенхе́ма – один из старейших алгоритмов в компьютерной графике, определяющий, какие точки двумерного растра нужно закрасить, чтобы получить близкое приближение прямой линии между двумя заданными точками.

Инкрементные алгоритмы выполняются как последовательное вычисление координат соседних пикселов путем добавления приращений координат. Приращения рассчитываются на основе анализа функции погрешности. В цикле выполняются только целочисленные операции сравнения и сложения/вычитания без использования умножения и деления.

Это позволяет повысить эффективность использования цифровых ЭВМ, которые, как раз, и отточены под целочисленные вычисления. Достаточно заметить, что y уменьшается от y₀ и за каждый шаг мы добавляем к x единицу и добавляем к y значение наклона 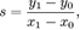которое можно вычислить заранее. Более того, на каждом шаге мы делаем одно из двух: либо сохраняем тот же y, либо уменьшаем его на 1 [10].

Существует обобщение алгоритма Брезенхэма для построения кривых 2-го порядка.

Алгоритм Брезенхема вывода окружности

Для вывода контура круга можно использовать соотношение между координатами X и Y для точек окружности X²+Y²=R² и построить алгоритм прямого вычисления координат. Однако в этом случае необходимо вычислять квадратный корень (как элемент бесконечной последовательности приближений).

Алгоритм вывода окружности пошагово генерирует очередные точки окружности, выбирая на каждом шаге для занесения пикселя точку растра P_i(X_i,Y_i), ближайшую к истинной окружности, так чтобы ошибка: E_i(P_i)=(X_i²+Y_i²) - R² была минимальной. Причем, как и в алгоритме Брезенхема для генерации отрезков, выбор ближайшей точки выполняется с помощью анализа значений управляющих переменных, для вычисления которых не требуется вещественной арифметики. Для выбора очередной точки достаточно проанализировать знаки.

Для простоты и без ограничения общности генерируют 1/8 окружности, центр которой лежит в начале координат. В вычислениях используется свойство окружности, что после закрашивания на экране пикселя самой верхней точки окружности на 1/8 ее части следующий пиксель, который необходимо закрасить может быть только один из двух соседних – справа или справа снизу. Остальные части окружности могут быть получены последовательными отражениями.

Аналогично можно построить эллипс.

Алгоритм Ву – это алгоритм разложения отрезка в растр со сглаживанием. Был предложен У Сяолинем (Xiaolin Wu, отсюда устоявшееся в русском языке название алгоритма) 1991 году. Алгоритм сочетает высококачественное устранение ступенчатости и скорость, близкую к скорости алгоритма Брезенхема без сглаживания.

Отличие состоит в том, что в алгоритме Ву на каждом шаге устанавливается не одна, а две точки. Например, если основной осью является Х, то рассматриваются точки с координатами (х,у) и (х, у+1). В зависимости от величины ошибки, которая показывает, как далеко ушли пиксели от идеальной линии по неосновной оси, распределяется интенсивность между этими двумя точками. Чем больше удалена точка от идеальной линии, тем меньше ее интенсивность. Значения интенсивности двух пикселей всегда дают в сумме единицу, то есть это интенсивность одного пикселя, в точности попавшего на идеальную линию. Такое распределение придаст линии одинаковую интенсивность на всем ее протяжении, создавая при этом иллюзию, что точки расположены вдоль линии не по две, а по одной.

7. Цвет в компьютерной графике

Современные САПР работают в цветном представлении изображений. Для описания цветов, которые получаются с помощью устройств, основанных на принципе излучения, используется аддитивная цветная модель RGB. В этой модели работают мониторы и бытовые телевизоры.

Кроме модели RGB применяется модель HSV, в которой цвет описывается следующими параметрами: цветовой тон H(Hue), насыщенность S(Saturation), яркость, светлота V(Value).

Для описания цвета при получении изображений на устройствах, которые реализуют принцип поглощения (вычитания) цветов используется субтрактивная цветовая модель CMYK. Цветовыми компонентами этой модели являются не основные цвета, а те, которые получаются в результате вычитания основных цветов из белого: Голубой(Cyan), Пурпурный(Magenta), Желтый(Yellow). Существуют также и другие цветовые модели.

8. Визуализация изображений. Основные понятия

Получение изображения на экране монитора персонального компьютера выполняется растровой графикой путем закрашивания всех пикселей в определенный цвет. На задание цвета для каждого пикселя экрана в памяти компьютера может быть отведено 1 или 2 бита. В соответствие с этим получено 2-х или 4-х цветное изображение (мониторы CGA, единственные, содержащие в своем названии слово «цветной», были именно 4-х цветными). При дальнейшем увеличении отведенной памяти в 1, 2, 3-х байта может быть передано 256, 65536 или 16 777 216 цветов [11]. Интересно, что человеческий глаз различает примерно 16 млн. оттенков цветов.

Возможное разрешение мониторов непрерывно растет и составляет 7680x4800 пикселов (при привычном 1280x1024, хотя лет 10 назад 800х600). При таком количестве точек, которые необходимо закрасить, без специальных средств компьютер можно было бы загрузить одной только этой задачей. Задача решается как аппаратно (совершенствованием видеокарт, процессоров и т.п.), так и программно путем разработки эффективных счетных алгоритмов.

9. Алгоритмы удаления скрытых линий и поверхностей

Задача удаления невидимых линий и поверхностей является одной из наиболее сложных в компьютерной графике. Алгоритмы удаления невидимых линий и поверхностей служат для определения линий ребер, поверхностей или объемов, которые видимы или невидимы для наблюдателя, находящегося в заданной точке пространства.

Сложность задачи удаления невидимых линий и поверхностей привела к появлению большого числа различных способов ее решения. Многие из них ориентированы на специализированные приложения. Наилучшего решения обшей задачи удаления невидимых линий и поверхностей не существует. Для моделирования процессов в реальном времени, например, для авиатренажеров, требуются быстрые алгоритмы, которые могут порождать результаты с частотой видеогенерации (30 кадр/с). Для компьютерной мультипликации, например, требуются алгоритмы, которые могут генерировать сложные реалистические изображения, в которых представлены тени, прозрачность и фактура, учитывающие эффекты отражения и преломления цвета в мельчайших оттенках. Подобные алгоритмы работают медленно, и зачастую на вычисления требуется несколько минут или даже часов. Строго говоря, учет эффектов прозрачности, фактуры, отражения и т.п. не входит в задачу удаления невидимых линий или поверхностей. Естественнее считать их частью процесса визуализации изображения. Процесс визуализации является интерпретацией или представлением изображения или сцены в реалистической манере.

Все алгоритмы удаления невидимых линий (поверхностей) включают в себя сортировку. Порядок, в котором производится сортировка координат объектов, вообще говоря, не влияет на эффективность этих алгоритмов. Главная сортировка ведется по геометрическому расстоянию от тела, поверхности, ребра или точки до точки наблюдения. Основная идея, положенная в основу сортировки по расстоянию, заключается в том, что чем дальше расположен объект от точки наблюдения, тем больше вероятность, что он будет полностью или частично заслонен одним из объектов, более близких к точке наблюдения. После определения расстояний или приоритетов по глубине остается провести сортировку по горизонтали и по вертикали, чтобы выяснить, будет ли рассматриваемый объект действительно заслонен объектом, расположенным ближе к точке наблюдения.

Алгоритмы удаления невидимых частей сцены можно классифицировать:

По выбору удаляемых частей: удаление невидимых линий, ребер, поверхностей, объемов.
По порядку обработки элементов сцены: удаление в произвольном порядке и в порядке, определяемом процессом визуализации.
По системе координат:
- алгоритмы работающие в пространстве объектов, когда каждая из N граней объекта сравнивается с остальными N-1 гранями (объем вычислений растет как N²),
- алгоритмы работающие в пространстве изображения, когда для каждого пикселя изображения определяется какая из N граней объекта видна (при разрешении экрана M×M объем вычислений растет как M² ×N).

Алгоритмы удаления линий

Применение - векторные устройства. Могут применяться и в растровых для ускорения процесса визуализации, но при этом не используется основное ценное качество растрового дисплея – возможность закраски поверхностей.

Наиболее известный ранний алгоритм – алгоритм Робертса (1963 г.). Работает с только выпуклыми телами в пространстве объектов. Каждый объект сцены представляется многогранным телом, полученным в результате пересечения плоскостей. Т.е. тело описывается списком граней, состоящих из ребер, которые в свою очередь образованы вершинами.

Вначале из описания каждого тела удаляются нелицевые плоскости, экранированные самим телом. Затем каждое из ребер сравнивается с каждым телом для определения видимости или невидимости. Т.е. объем вычислений растет как квадрат числа объектов в сцене. Наконец вычисляются новые ребра, полученные при протыкании телами друг друга.

Алгоритм плавающего горизонта чаще всего используется для удаления невидимых линий трехмерного представления функций, описывающих поверхность в виде: F(x, у, z) = 0.

Подобные функции возникают во многих приложениях в математике, технике, естественных науках и других дисциплинах.

Главная идея данного метода заключается в сведении трехмерной задачи к двумерной путем пересечения исходной поверхности последовательностью параллельных секущих плоскостей, имеющих постоянные значения координат х, у или z.

Алгоритм сначала упорядочивает плоскости z=const по возрастанию расстояния до них от точки наблюдения. Затем для каждой плоскости, начиная с ближайшей к точке наблюдения, строится кривая, лежащая на ней, т. е. для каждого значения координаты х в пространстве изображения определяется соответствующее значение y. Алгоритм удаления невидимой линии заключается в следующем. Если на текущей плоскости при некотором заданном значении x соответствующее значение у на кривой больше значения y для всех предыдущих кривых при этом значении x, то текущая кривая видима в этой точке; в противном случае она невидима.

Фактически этот алгоритм удаления невидимых линий работает каждый раз с одной линией.

Алгоритм удаления поверхностей с Z-буфером

Алгоритм предложен Эдом Кэтмулом и представляет собой обобщение буфера кадра. Обычный буфер кадра хранит коды цвета для каждого пикселя в пространстве изображения. Идея алгоритма состоит в том, чтобы для каждого пикселя дополнительно хранить еще и координату Z или глубину. При занесении очередного пикселя в буфер кадра значение его Z-координаты сравнивается с Z-координатой пикселя, который уже находится в буфере. Если Z-координата нового пикселя больше, чем координата старого, т.е. он ближе к наблюдателю, то атрибуты нового пикселя и его Z-координата заносятся в буфер, если нет, то ни чего не делается.

Главное преимущество алгоритма – его простота. Основной недостаток – большой объем требуемой памяти.

Алгоритм использующий список приоритетов

Алгоритмы, использующие список приоритетов, пытаются получить преимущество посредством предварительной сортировки по глубине или приоритету. Тогда можно записать все элементы в буфер кадра поочередно, начиная с элемента, наиболее удаленного от точки наблюдения. Более близкие к наблюдателю элементы будут затирать информацию о более далеких элементах в буфере кадра. Эффекты прозрачности можно включить в состав алгоритма путем не полной, а частичной корректировки содержимого буфера кадра с учетом атрибутов прозрачных элементов.

Для простых элементов сцены, например для многоугольников, этот метод иногда называют алгоритмом художника, поскольку он аналогичен тому способу, которым художник создает картину. Сначала художник рисует фон, затем предметы, лежащие на среднем расстоянии, и, наконец, передний план [12].

Алгоритм разбиения области Варнока

Алгоритм работает в пространстве изображения и анализирует область на экране дисплея (окно) на наличие в них видимых элементов. Если в окне нет изображения, то оно просто закрашивается фоном. Если же в окне имеется элемент, то проверяется, достаточно ли он прост для визуализации. Если объект сложный, то окно разбивается на более мелкие, для каждого из которых выполняется тест на отсутствие и/или простоту изображения. Рекурсивный процесс разбиения может продолжаться до тех пор пока не будет достигнут предел разрешения экрана [1, 13, 14].

Алгоритм определения видимых поверхностей путем трассировки лучей

Оценка эффективности всех перечисленных алгоритмов удаления невидимых поверхностей, зависит от определенных характеристик когерентности той сцены, для которой ведется поиск ее видимых участков.

В отличие от них трассировка лучей является методом грубой силы (метод, не учитывающий специфику обрабатываемого объекта). Главная идея, лежащая в основе этого метода, заключается в том, что наблюдатель видит любой объект посредством испускаемого неким источником света, который падает на этот объект и затем каким-то путем доходит до наблюдателя. Свет может достичь наблюдателя, отразившись от поверхности, преломившись или пройдя через нее. Если проследить за лучами света, выпушенными источником, то можно убедиться, что весьма не многие дойдут до наблюдателя. Следовательно, этот процесс был бы вычислительно неэффективен. Аппель первым предложил для определения видимых или скрытых поверхностей отслеживать (трассировать) лучи в обратном направлении, т.е. от наблюдателя к объекту.

Впоследствии Кей и Уиттед реализовали алгоритмы трассировки лучей с использованием общих моделей освещения. Эти алгоритмы учитывают эффекты отражения одного объекта от поверхности другого, преломления, прозрачности и затемнения [15].

10. Очень кратко о презентационной графике

При формировании изображения сцен в презентационной графике используют законы геометрической оптики, преломляющие свойства материалов, эффекты смешения цветов и т.д. Производится также устранение ступенчатости.

Методы закрашивания объектов, моделируемых многогранниками и полигональными сетками, основаны на моделях отражения света. При изображении объектов обычно моделируют сочетание зеркального и диффузного рассеивания в пропорции, характерной для конкретного материала. Интенсивность отраженного света можно определить как сумму диффузного и зеркального компонентов (из физики). С учетом рассеяния света с расстоянием I_отр = I_a K_a+I (K_d cos q + K_s cos ^pa)/(R+k),

где константы K_d, K_s определяют отражательные свойства материала. R – расстояние от центра проекции до поверхности, k – константа, подбираемая эмпирически.

Этот метод предназначен для создания иллюзии гладкой криволинейной поверхности, описанной в виде многогранников или полигональной сетки с плоскими гранями. Простое увеличение число граней приводит к существенному замедлению визуализации. Преодолеть это противоречие призваны методы Гуро и Фонга.

Метод Гуро основывается на идее закрашивания каждой плоской грани не одним цветом, а плавно изменяющимися оттенками, вычисляемыми путем билинейной интерполяции цветов примыкающих граней. Существенным недостатком метода Гуро является невозможность получения качественных бликов на блестящих поверхностях.

Закраска Фонга требует больших вычислительных затрат, однако она позволяет разрешить многие проблемы метода Гуро. При закраске Гуро вдоль сканирующей строки интерполируется значение интенсивности, а при закраске Фонга – вектор нормали. Затем он используется в модели освещения для вычисления интенсивности пикселя. При этом достигается лучшая локальная аппроксимация кривизны поверхности и, следовательно, получается более реалистичное изображение. В частности, правдоподобнее выглядят зеркальные блики [16].

Выводы

Можно говорить, что обстоятельно исследованы сегменты геометрических преобразований и описаний кривых и поверхностей. Также изучены, но все еще продолжают развиваться методы растрового сканирования, отсечение, удаление линий и поверхностей, цвет, закраска, текстура и эффекты прозрачности.

Нужно ли знание внутренних алгоритмов работы графических компьютерных программ САПР инженеру-конструктору? В профессиональной деятельности – навряд ли. Но для грамотного преподавателя для расширения кругозора и эрудиции на понятийном уровне ознакомление с ними необходимо. Кроме того в программах компьютерной графики (возможно не во всех) предусматривается возможность для программирования на уровне пользователя. Использование такой возможности в сочетании со знанием внутренних алгоритмов может повысить производительность и значительно расширить возможности использования программ. Есть примеры, когда преподаватели, владеющие графическими программами на уровне программирования в них, успешно передают эти знания своим студентам [7].

Ну и, конечно же, алгоритмы компьютерной геометрии – это один из разделов математики, которую по меткому выражению М.В.Ломоносова «уже затем учить надо, что она ум в порядок приводит».

Лепаров Михаил Николаевич (18 февраля 2016 г. 15:04)	Здравствуйте, уважаемый Алексей Алексеевич! Спасибо большое за обзорной доклад. Согласен с Вами, что для грамотного преподавателя нужно знать в общем что происходить в компютере. Кроме того преподавателя надо знать так же и научные методы, използуваемые в конкретный вычислительный софтуер (напр. при расчета напряжений и деформаций). К рассматриваемыми Вам вопросам я добавил бы „классификация геометрических моделей”. Пожалуйста, извините мой русский. С уважением
Головнин Алексей Алексеевич (18 февраля 2016 г. 23:45)	Здравствуйте уважаемый Михаил Николаевич! Спасибо за Ваше внимание к моему докладу и высказанное замечание. Ввиду поставленных ограничений по объему 15-ю страницами, да и просто по соображениям разумного предела, информацию о многих алгоритмах компьютерной графики пришлось опустить. Можно сказать, что в докладе авторский только выбор алгоритмов для их анализа. Делалось это в основном осознанно, как например не упомянута параметризация (в программах учебных дисциплин отнесена не к геометрии, а к САПР). Как сказано в начале доклада, материал подбирался, в том числе для сравнения с методами ручного черчения. Что же касается классификации геометрических моделей, то здесь с самого начала у меня было чувство, что сказано слишком кратко. Склоняюсь к тому, что можно было бы дать классификацию по внутреннему представлению, два или три пункта, в разных источниках по-разному. В частности в выбранном для анализа источнике [1] выделены два основных типа представлений 3D моделей: · граничное, когда в модели хранятся границы объекта, например, вершины, ребра, грани, · в виде дерева построения, когда хранятся базовые объекты (призма, пирамида, цилиндр, конус и т.п.) из которых формировалось тело и использованные при этом операции; в узле дерева сохраняется операция формирования, а ветви представляют объекты. При этом возможно преобразование из одной модели в другую. Еще раз с уважением и благодарностью
Попов Евгений Владимирович (26 февраля 2016 г. 0:05)	Честно говоря не очень понимаю зачем нужно в научной статье описывать вещи, которые давным-давно всем известны и описаны много раз в статьях, учебниках и книгах, и даже намного лучше (см. например замечательную книгу - настольную даже для профессионалов до сих пор: Роджерс Д. Алгоритмические основы машинной графики. М., Мир, 1989. 504с и многие другие источники). Я уж не говорю вообще об ошибках, которые понимающий специалист не имеет право допускать. Чего стоит например употребление связки 3D компьютерная графика. Известно, что графика вообще - вещь двумерная (см. Википедию: Графи́ка (др.-греч. γρᾰφικός — письменный, от др.-греч. γράφω — записывать, писать) — вид изобразительного искусства, использующий в качестве основных изобразительных средств линии, штрихи, пятна и точки. То есть, носителем здесь является пространство 2D по определению). Компьютерная графика - это наука разрабатывающая методы и средства формирования изображений с помощью средств визуализации компьютеров. Носитель компьютерного образа это монитор, который при всем желании нельзя считать трехмерным. Вот МОДЕЛИ могут иметь любую размерность, но не графика. Вот когда мы будем иметь доступ к 3D устройствам, которые пока страшно дороги и недоступны (к сожалению) вот тогда и будем говорить о 3D компьютерной графике. К тому же неясно откуда взялась информация, что существует некая отдельная "фрактальная компьютерная графика". Здесь закрадывается страшное подозрение, что автор вообще не понимает существа дела. Фрактальными могут быть только ГЕОМЕТРИЧЕСКИЕ МОДЕЛИ. Я с большим бы интересом взглянул бы на "фрактальный монитор". Вот векторные и растровые мониторы - встречал, "фрактальных" же не видел...
Головнин Алексей Алексеевич (27 февраля 2016 г. 0:51)	Уважаемый Евгений Владимирович. «Не очень понимаю …» - когда мне студенты говорят «а я не понимаю», я им отвечаю, не всем конечно, а в отдельных случаях, что не все люди одинаковые и не каждый должен понимать. По существу – обоснованию актуальности темы доклада я посвятил целую страницу, повторяться не буду. Доклад методический обзорный, а не научный. Это было явно указано . «Чего стоит употребление связки 3D компьютерная графика» - я не нашел этого в своем докладе. Даже запускал для этого поиск. Возможно, вы переиначили мое упоминание о четвертом виде графики? Я упомянул о нем в кавычках одним предложением. Я не склонен так считать, но вообще-то учебные курсы носят название «Компьютерная графика» и в них мы преподаем, в том числе и геометрическое моделирование, но когда мы говорим 3D, тоже друг друга понимаем. Новая область знаний имеет неустоявшуюся терминологию. Об этом мы часто говорим на нашей конференции, в том числе и в этом году. То же по поводу «фрактальная компьютерная графика". Я объяснил в докладе, почему я не указал в списке литературы, в том числе и «настольную даже для профессионалов» книгу. Хотя, вне всякого сомнения, надо знать свои корни, но это вопрос, на мой взгляд, больше по истории науки. Добавлю, что в ней нет ничего про фрактальную графику. А термин этот общепринят, можно убедиться, набрав в поиске – 203 тыс. ответов только в русскоязычном поисковике, несмотря на узкую специальность термина. Вместе с тем ваше мнение понял, в дальнейшей работе приму во внимание, наряду с мнением других, не менее авторитетных коллег. «Вот когда мы будем иметь доступ к 3D устройствам, которые пока страшно дороги и недоступны (к сожалению) вот тогда и будем говорить о 3D компьютерной графике.» Непонятна логика сказанного. По-вашему, если учитель географии лишен возможности по желанию бывать в Антарктиде он не должен о ней и говорить своим ученикам? Не ко всему, чему, мы учим студентов, мы имеем доступ. Лично я говорю своим студентам о «3D устройствах». Они пишут мне рефераты на эту тему. Если 3D устройства для вас «недоступны», то, наверное, не надо давать на этом основании вообще какие либо советы. Согласитесь, что более уместно в таком случае попросить поделиться информацией тех, для кого они «доступны».
Шацилло Людмила Анатольевна (27 февраля 2016 г. 1:15)	Добрый вечер, профессор! Насколько я понимаю, Алексей Алексеевич пояснил, что знание внутренних алгоритмов компьютерных программ для преподавателя ИГ в порядке расширения кругозора и эрудиции на понятийном уровне необходимо. С этой целью и написана статья. Чтобы учили не только потребителей технологий. Это первое. Второе. Полагаю, что о фракталах как множествах, обладающих масштабной инвариантностью, автору статьи известно. И не только в части геометрии. Страшного не подозревайте. Любимая всеми Википедия и сайты интернета, начиная с сайтов для учителей, как раз пестрят терминами "фрактальная компьютерная графика". На полях конференции (2015г.) и в №3 ГиГ (2015г.) все мы познакомились с очень интересными работами по фрактальной геометрии. А смешивать при сравнении вещи разных модальностей – тоже не высший пилотаж! С уважением, Л.А.
Пирогова Марина Аркадьевна (27 февраля 2016 г. 5:54)	Уважаемый Алексей Алексеевич! Откровенно говоря, поскольку мы уже в другой дискуссии касались Вашего доклада, мне не хотелось в этом обсуждении включаться со своими претензиями к нем и здесь. Однако завязавшаяся дискуссия показалась мне весьма полезной, и я здесь вынуждена полностью поддержать лаконичное сообщение уважаемого коллеги Попова Е. В. Вы пишете, что Ваш доклад не претендует на научность, он – «методически-обзорный». Цель значима, но выбранные для ее достижения средства – по результату - скорее вредят прежде всего методической составляющей, чем помогают специалистам в области преподавания геометрии, использующим в своей практике современные средства автоматизации, разобраться и понять, что же там за кнопками. Из предыдущих наших с Вами дискуссий Вы, надеюсь, поняли, что по моему мнению Вы несколько путаете собственно алгоритмы (способы представления объектов) машинной графики, которые можно разбить на векторные и растровые (у Вас это называется «видами машинной графики»), с задачами и алгоритмами визуализации того, что я уже неоднократно называла внутримашинным представлением геометрических 2D-и 3D-моделей. Во всяком случае, материал раздела 1., к сожалению, не поможет желающим разобраться «что там за кнопками» в любой САПР или какого-нибудь ACDSee. Возможно, виной тому – ограниченный объем доклада, хотя по моему мнению можно было бы по-другому расставить в нем акценты. Например, не совсем оправдано в заявленном контексте столь пристальное внимание однородным координатам, или – алгоритмам удаления невидимых линий и поверхностей. Или тот факт, что в Вашем докладе такие темы, как визуализация, методы закраски, АУНП, цветовая модель разнесены в разные разделы. А ведь и УНП, и закраска, и определение цвета – это все ни что иное, как этапы визуализации. Не могу не согласиться с критикой и по поводу упоминания в одном ряду с векторной и растровой графикой пресловутой фрактальной графики. Прав Евгений Владимирович – первое, что приходит в голову при упоминании «фрактальная», так это – модель. Действительно, это сегодня достаточно модная «фишка» (прошу прощения за жаргонизм), активно используемая в рекламе, для создания исключительной красоты узоров, оформления сайтов и дискотек. Ну и для визуализации турбулентных потоков, конечно. А еще – при создании изображений в различных графических реализациях облаков и гор. Я немного иронизирую, и Вы правы – есть источники, где эти три «графики» стоят в одном ряду (Снижко, в частности), но я бы их рядом не ставила. Здесь уже указывалось, и Вы сами с этим согласились, что материал доклада существенно бы выиграл, если бы Вы уделили внимание классификации геометрических моделей в САПР, рассказалаи об основным алгоритмах их построения (вот уж точно – «а что там, за кнопками»), реализованных в геометрических моделлерах. В то же время, дважды (при описании кривых и поверхностей) Вы обращаетесь к В-сплайнам и NURBS. И пара конкретных замечаний. Вы не согласились с замечанием о неуместном использовании 3D- машинной графики: «Чего стоит употребление связки 3D компьютерная графика» - я не нашел этого в своем докладе…Возможно, вы переиначили мое упоминание о четвертом виде графики? Я упомянул о нем в кавычках одним предложением. Я не склонен так считать» Вообще эту часть Вашего доклада трудно как-то переиначить, а замечание про отдельный вид графики, куда относят 3D- или трехмерную графику, не закавычено: Также в отдельный, четвертый, вид графики часто выделяют и 3D- или трёхмерную графику. «От двухмерной она отличается тем, что подразумевает построение проекции трехмерной модели сцены (виртуального пространства) на плоскость» [4]. Вы пишете далее: «Новая область знаний имеет неустоявшуюся терминологию. Об этом мы часто говорим на нашей конференции, в том числе и в этом году». Еще раз вынуждена обратить Ваше внимание – эта «новая» область знаний существует уже достаточно давно, и профессионалам в мире хватило прошедших 50 лет для того, чтобы терминология в ней, области этой, устоялась. Если в курсах «Компьютерная графика» Вы преподаете и геометрическое моделирование (мы так это в отдельных специальных курсах преподаем), то по моему твердому разумению не стоит столь «творчески» подходить к терминологии возможно для Вас и Ваших коллег – новой, но в принципе – уже довольно традиционной области знаний. Первыми пострадавшими здесь окажутся обучающиеся – весьма вероятно будущие пользователи высокотехнологичных современных CAD/CAM/CAE/PLM- программно-аппаратных комплексов на производстве. И еще я бы предостерегла Вас от такого аргумента, как сотни тысяч ссылок, которые Вы получаете в поисковых системах по ключевым словам. Это очень лукавые цифры. Простой пример. Замысловатые формулировки из Вашего доклада про проектирование (мат.) в смысле проецирование, если запустить поиск по части предложения «Важнейшей операцией при визуализации трехмерной графики является проектирование (мат.). Проектирование...» даст Вам с десяток ссылок, причем практически ни в одной из них не будет указан источник, которым, как я могу предположить, служит книжка Снижко. А может быть и нет. То же и про фракталы. 203 тысячи ссылок еще не означают, что можно безо всяких сомнений отнестись к тому, Что это – тот «вид компьютерной графики», который следовало бы в обзорном докладе ставить в один ряд с векторной и растровой графикой. Или таковым является в первую очередь для ... разработчиков компьютерных игр. С уважением, Пирогова М.А.
Головнин Алексей Алексеевич (27 февраля 2016 г. 8:02)	Уважаемые коллеги, по дороге с работы зашел в лабораторию геометрического прототипирования, в другом здании, одиннадцать 3D принтеров и сканеров, фото оборудования лаборатории привожу. Переносной сканер сфотографировал в своих руках. Уговорил организаторов и работников лаборатории подготовить доклад. Надеюсь, они успеют.
Дударь Елена Сергеевна (27 февраля 2016 г. 10:03)	Уважаемый, Алексей Алексеевич! Всегда с удовольствием знакомлюсь с Вашими публикациями, они вызывают интерес, наталкивают на размышления. Являясь пользователем программного продукта, прежде всего, задумываешься о тех «рамках», которые ограничивают область его применения. Меня заинтересовало положение о том, что «в декартовых координатах невозможно описать бесконечно удаленную точку». Математика оперирует абстрактными понятиями, очевидно, что и бесконечность – понятие идеальное. Можно ли, в таком случае, его где-либо реализовать? Речь идет об актуальной бесконечности? Буду признательна за ссылки на литературу по данному вопросу. Применяете ли Вы знания алгоритмов в практической реализации студенческих работ на занятиях по компьютерной графике, в решении олимпиадных задач или проектных разработках? С пожеланиями удачи, Елена С. Дударь.
Попов Евгений Владимирович (27 февраля 2016 г. 11:53)	или .
Шацилло Людмила Анатольевна (27 февраля 2016 г. 13:35)	Евгений Владимирович! В этой ситуации можно ли надеяться, что Вы напишете по существу темы лучше и доходчивей для всех фанатов А.А. и остальной части образовательного сообщества в пределах временных рамок этой конференции? В предвкушении, Л.А.
Попов Евгений Владимирович (27 февраля 2016 г. 14:56)	или .
Шацилло Людмила Анатольевна (27 февраля 2016 г. 15:37)	Евгений Владимирович! А я так надеялась, что Вы как высокий профессионал (в чем я никоим образом не сомневаюсь) обогатите наше недознание и повысите наш тезаурус по данному вопросу. Ну, что ж, не судьба... С уважением, Л.А.
Попов Евгений Владимирович (27 февраля 2016 г. 16:51)	. или
Тихонов-Бугров Дмитрий Евгеньевич (27 февраля 2016 г. 16:53)	Уважаемый Евгений Владимирович, согласен, что про "закнопочное пространство" должен писать специалист в этой области. Однако, дискуссия принимает грубоватый оборот. В русской словесности есть простое выражение несогласия с собеседником: Вася, ты не прав!
Головнин Алексей Алексеевич (27 февраля 2016 г. 22:26)	Здравствуйте Марина Аркадьевна! Я тоже считаю получившееся у нас с Вами общение полезным. О консенсусе мы с Вами уже говорили. Давно читал, что если бы научные вопросы принимались консенсусом, то мы бы до сих пор считали, что Земля покоится на трех китах. Просто считаю, что мне полезно было прикоснуться к Вашим знаниям, как из смежной области, надеюсь и Вам к моим и Ваш интерес к моему докладу искренний. К тому же с Вами мне просто приятно общаться, а это немаловажный фактор в процессе обмена информацией. «я уже неоднократно называла внутримашинным представлением геометрических 2D-и 3D-моделей» - я тоже неоднократно говорил, что, на мой взгляд, модель одна, или Вы говорите о разных моделях, которые обрабатываются одной программой в разное время? Обмен мнениями состоялся, но я, несомненно, не спеша перечитаю наши беседы по окончании конференции и может быть, в ваших вопросах увижу что-то, что сейчас не так понимаю. «Возможно, виной тому – ограниченный объем доклада» - я стремился именно в ограниченном объеме собрать основные алгоритмы компьютерной геометрии и графики. На 15 страницах материал 200 умноженное на (3-4 и более) страниц. Это не учебник, но и не оглавление к нему. Как я уже говорил в докладе авторский - отбор информации. Выбор материала определялся следующим основным правилом: взгляд преподавателя по инженерной графике (не математика) на алгоритмы решения «наших» задач «математиками». Своих выводов старался не делать, иначе можно было бы написать, что методы НГ в компьютерной графике не применяются. Или в более жёсткой форме – повторить известный вывод о том, что аналитическая геометрия победила начертательную. Надеялся на то, что читатель сам сделает свои выводы, как говорится информации достаточно. Но и конечно самое главное, надеялся, что для кого-то мой скромный труд станет началом путешествия в красивый мир алгоритмов компьютерной графики (геометрии). Два примера для подтверждения актуальности работы привел в смягченной форме (авторское), может быть авторы высказываний и не узнают их, не приводил источников, считаю эти два примера ошибочными, но цели конфронтации не ставил, считаю, что такая цель неправильная, а мнение авторов этих высказываний их правом. Впрочем, как и свое право на высказывание мнения. Собственно мы и собрались для обмена накопленным за год опытом, а не для выслушивания безапелляционных заявлений типа «автор вообще не понимает существа дела». Еще по поводу того, что не тот автор написал такую важную статью. Сутрирую чтобы было понятно, о чем речь: Как это Пушкин посмел написать о Евгении Онегине. Уважаемые носители такой идеи, позвольте спросить, а где вы раньше были? Надеюсь правило приоритета в науке никто не отменил, аналогичной работы я не нашел, если у кого то есть свое мнение на объявленную тему, то вполне можно изложить мнение в своей статье, но только теперь уже с учетом опубликованного материала. Разве не так? Попутно обратим внимание на принятые в научном мире традиции научной дискуссии: задать вопрос(ы), выслушать ответ и высказать свое мнение. Слово автора завершает дискуссию. Кроме того, есть правила просто хорошего тона, а еще проявления интеллигентности. Ваш «уважаемый коллега Попов Е. В.» не первый и не единственный доктор наук, профессор на этой конференции. До него были и есть, их не так много, но они задают тон и являют пример (конечно, не только они). Присмотритесь к их манерам изложения информации, ведения дискуссии, даже аватаркам, глядя на которые можно как будто беседовать с ними, глядя им в глаза, и сравните с его. Думаю, Вы заметите большую разницу. «Например, не совсем оправдано в заявленном контексте столь пристальное внимание однородным координатам, или – алгоритмам удаления невидимых линий и поверхностей». – неужели Вы искренне это говорите? В любом случае эта оценка субъективна, но как, например, Вы объясните мне, что для преобразования трех координат используются четырехмерные матрицы, с учетом того, что я, например, никогда раньше не изучал и не слышал по работе об однородных координатах? (инженер-механик, преподаватель инженерной графики, и думаю, я не исключение в ряду коллег, собравшихся поделиться своим опытом). Подробное рассмотрение удаления невидимых линий – специально обратить внимание на этом простом примере, что методы определения видимости очень сильно отличаются от метода конкурирующих точек из НГ. Надеюсь, вы помните этот материал. По своему опыту, пришел на кафедру ИГ через 18 лет после окончания ВУЗа, по НГ имел «5», но не помнил. Если помните, то непонятно, почему Вас смущает этот момент? Напрямую об этом не писал, причину объяснил выше. «в Вашем докладе такие темы, как визуализация, методы закраски, АУНП, цветовая модель разнесены в разные разделы.» - мне показалось так удачнее по тем же причинам. «Прав Евгений Владимирович – первое, что приходит в голову при упоминании «фрактальная», так это – модель». Первое – в Вашем вопросе надо понимать правильное? Еще - Ваша формулировка не допускает сомнения, тем более, если я усомнюсь, то я один, а вас двое. Но я бы сказал, что это, в первую очередь – не модель, а метод. В частности вы не упомянули очень важного направления развития фрактальной графики-геометрии – это архивация. Как тут быть с моделью? «В то же время, дважды (при описании кривых и поверхностей) Вы обращаетесь к В-сплайнам и NURBS.» - можно идти от частного к общему, а можно от общего к частному. Это выбор автора. Мне показалось, что для неспециалиста лучше идти от частного к общему – постепенность и последовательность познания. «Вообще эту часть Вашего доклада трудно как-то переиначить, а замечание про отдельный вид графики, куда относят 3D- или трехмерную графику, не закавычено:». 1. Настаиваю на том, что Вы вместе с Вашим «уважаемым коллегой Поповым Е. В.» ошибочно приписываете мне чужие взгляды, которых я не разделяю при помощи подтасовок или просто так; 2) Разве во фразе, сформулированной в третьем лице «Также в отдельный, четвертый, вид графики часто выделяют и 3D- или трёхмерную графику.» не содержится авторского отношения к формулировке? 3) Следующее предложение взято мной в кавычки, и это означает, что это не мое, а я мало чего в тексте еще брал в кавычки; 4) Приписывание мне таких взглядов сопровождается обвинениями в разных грехах, а на каком основании Вы не разрешаете авторам такого деления, а их немало, иметь свое мнение? 5) Даже если это не правильно, Вам не кажется, что надо только сказать спасибо тем, кто написал для нас книги о 3D компьютерной графике? Если считаете, что так нельзя – пишите как надо. «по моему твердому разумению не стоит столь «творчески» подходить к терминологии». – Что именно, по Вашему мнению, я придумал или применил не по назначению? Вы знакомились с моими другими докладами на этой конференции? А мои выступления по Вашему с уважаемыми Вашими коллегами очень полезному и нужному докладу Вы хоть помните? Я вообще-то сам себя позиционирую как поборника грамотной терминологии. Но никогда не предъявлял обвинений носителям «неправильной» терминологии, если, по сути, информация полезна для меня, а так было всегда. Насчет интернета – согласен, лишнее, но книжки то Вы не хотите брать в учет. Вообще можно до бесконечности об одном и том же. «Что это – тот «вид компьютерной графики», который следовало бы в обзорном докладе ставить в один ряд с векторной и растровой графикой.» – Я написал о фрактальной графике всего одно предложение. Вы считаете, лучше было вообще не говорить, будто нет ее? Это Ваше мнение, если будете писать на эту тему – напишите как надо. Марина Аркадьевна, я благодарен Вам за внимание к моей работе. Постарался внимательно прочитать Ваши вопросы и максимально тщательно ответить на них, если на какие-то вопросы не ответил, или просто их пропустил, то не нарочно. В завершение напомню, что надеюсь услышать Ваши ответы на мои вопросы по поводу Вашего высказывания «Например, не совсем оправдано в заявленном контексте столь пристальное внимание однородным координатам, или – алгоритмам удаления невидимых линий и поверхностей». Получилось длинно, но и вопросов много. С уважением
Головнин Алексей Алексеевич (29 февраля 2016 г. 0:56)	Елена Сергеевна, я тоже всегда с интересом жду Ваши доклады и с большим удовольствием читаю Ваши выступления. Алгоритмы компьютерной геометрии и графики я преподавал в читаемом мной с 2005 по 2015 студентам специальности 230201 - «Информационные системы и технологии» очной и заочной форм обучения курсе «Компьютерная геометрия и графика» в объеме - 32 часа лекции и 32 часа лабораторный практикум. Этот доклад не мог появиться без такого опыта. С учетом высказанных, особенно критических, замечаний коллег попробую еще раз сформулировать сделанное в процессе написания доклада наблюдение. Для решения собственно геометрических задач в графических программах САПР используется в основном известный математический аппарат аналитической геометрии, развитие получили востребованные сплайны. Также однородные координаты из проективной геометрии. Для получения изображения на экране монитора разработаны специальные методы, учитывающие физические принципы работы мониторов. Их алгоритмы всегда оказываются неожиданными и очень остроумными, как например метода Брезенхема для окружности, методы Гуро и Фонга. Бурно развиваются методы визуализации, которые оставлены за рамками доклада. Для начального знакомства с однородными координатами мне понравилась ссылка на сайте, как я понял, Александра Каленюка https://habrahabr.ru/post/126269/ Также настольной книгой для меня год назад стала книга В.А. Маневич, И.И. Котов, А.Р. Зенгин «Аналитическая геометрия с теорией изображений» 1969., показавшаяся мне очень доступной по изложению и в которой уделено большое внимание физической сущности излагаемого материала. По ФГОСам третьего поколения эта дисциплина исключена из учебных планов студентов ИСТ, но теперь изучается математиками с соответствующей корректировкой содержания. С уважением
Пирогова Марина Аркадьевна (29 февраля 2016 г. 3:46)	Алексей Алексеевич, добрый вечер. Прочитала Ваш пространный ответ, ряд тезисов в нем явно не ко мне относятся. А те, что - относятся, уже неоднократно мы с Вами обсуждали. И здесь и в дискусси по другому докладу. Повторяться смысла не вижу. Что касается Ваших конкретных недоумений по поводу моей искренности, то в общем их не принимаю. Я всегда говорю вполне искренне, и в данном конкретном случае имела в виду только то, что по моему мнению в обзорном докладе об актуальных на сегодня базовых алгоритмах МГ я бы рекомендовала иначе расставить акценты, перераспределить объем и степень подробности изложения ряда его, доклада, частей. Каких - написано выше. Спасибо, Пирогова М.А.