Уважаемые коллеги!

Не вижу особого смысла (разве ради проформы) в составлении решения конференции: в МОН, скорее всего, его читать не будут и, тем более, рассчитывать на его реализацию не приходится. Надеяться на «молчаливую методическую комиссию» также нет смысла.

Поэтому предлагаю, как сейчас принято на высшем уровне, организовать общественный орган для разработки концепции преподавания начертательной геометрии, инженерной и компьютерной графики в современных условиях (содержание, разумное сочетание внутрипредметных связей, программы, темы заданий и т.д.)

Целесообразно создание трех рабочих групп:

1. начертательная геометрия (с моей точки зрения хорошим руководителем этой группы был бы проф. Н.А. Сальков);
2. инженерная графика (руководитель …);
3. компьютерная графика (руководитель …).

Каждый руководитель группы набирает свою команду профессионалов.

Так как мы должны готовить специалистов, квалификация которых удовлетворяет требованиям заказчика, то по идее следовало бы провести анкетирование руководителей ведущих фирм, предприятий и т.д. Но этот процесс трудоемкий и долгий. Поэтому роль заказчика могла бы выполнить команда научных руководителей во главе с представителем нашей дисциплины в ВАКе проф. С.И. Ротковым. Кому, как не этой команде, знать актуальность тем исследований, необходимый уровень знаний выпускников ВУЗов для решения задач инженерной геометрии, владения компьютерной графикой? Представляется, что эта команда сформулирует «технические задания» перечисленным выше трем рабочим группам.

И, наконец, координатором этого проекта предлагаю проф. И.Д. Столбову: она проявила себя с наилучшей стороны в организации наших интернет-конференций.

Только после проведения такой работы, на мой взгляд, есть смысл выйти на УМО.

С уважением Г.С. Иванов

Александр Львович!

Где Вы вычитали, что я критикую 3D? Я всего лишь против догматического, ненаучного противопоставления различных видов изображений, получаемых по схеме классического метода двух изображений! (Прочитайте стаью В.А. Короткого «Учебное задание “пространства различной размерности”», в которой он грамотно объяснил суть вопроса). Более того, я убежденный сторонник изучения начал многомерной (nD) геометрии для установления межпредметных связей между начертательной геометрией, линейной алгеброй и смежными разделами высшей математики. Там ведь тоже надо уметь изображать! Вспомните, с чего начался наш разговор на этой конференции.

Я считаю, что мнение о начертательной геометрии лишь как об обеспечивающей дисциплине курсов инженерной и компьютерной графики, принижает ее роль в системе высшего образования. Результаты исследований, выполненных за последние 50-60 лет в рамках специальности 05.01.01, на мой взгляд, убедительно свидетельствуют о возможностях инженерной геометрии, в состав которой органично входит начертательная геометрия.

Г.С. Иванов.

Александр Львович!

Давайте не будем требовать извинений друг от друга! Мой резкий ответ Вы спровоцировали своими словами «… является бантиком для украшения работы и придания ей наукообразия».

Далее по существу. Согласен с Вами: «коллинеарность» здесь не причем. Это предположение вызвали Ваши слова «проверка на конгруэнтность». Термин «конгруэнтность» является синонимом слова «равенство» (см. О.В. Мантуров и др. Толковый словарь математических терминов. М., Просвещение, 1965). У меня, естественно, возник вопрос: «При чем здесь равенство?» И я предположил, что Вы имеете в виду принадлежность (коллинеарность) трех точек пересечения образующей с направляющими. (у Вас ведь два тела пересекаются по линии – Autocad здесь не причем). А Вы, оказывается, под этими словами имели в виду существование конструируемой (из конгруэнции) поверхности действительных образующих. Только после ссылки на учебник С.А. Фролова в Вашем последнем комментарии я понял суть Ваших заблуждений, и, как следствие, наших разногласий.

Сначала небольшой исторический экскурс. Учебник С.А. Фролова я очень внимательно прочитал сразу же после выхода в свет первого издания в 1978 году. Экземпляр учебника с моими многочисленными замечаниями (подстрочными и на полях) почти на каждой странице, вернул автору. Возможно, этот экземпляр сохранился у Андрея Сергеевича, сына С.А. Фролова. С тех пор, образно говоря, этот учебник до сегодняшнего дня в руки не брал и, естественно, в целом забыл и его содержание, и свои замечания.

Теперь несколько слов к сведению Александра Владиславовича. В Советском Союзе, а сейчас в России и странах ближнего зарубежья, существовали(ют) две школы начертательной геометрии (НГ): гордоновская и четверухинская. Школу В.О. Гордона отличает догматическая позиция: НГ – это сугубо графическая дисциплина, аналитика (тем более мнимости) – это математика; многие представители этой школы геометрию отождествляют с графикой; завет Г. Монжа о полезности совместного изучения «геометрии и алгебры» не признают. Кстати, теперь и в школе учат, что квадратное уравнение, имеющее отрицательный дискриминант, не имеет решения.

Школа Н.Ф. Четверухина (доктора физмат наук, академика АПН СССР), следуя заветам Г.Монжа, считает, что в геометрии (в том числе и в НГ – как разделе геометрии) есть два противоположных, но взаимодополняющих метода исследования: синтетический (конструктивный, в частности, графический) и аналитический.

Проф. С.А. Фролов, А.Л. Хейфец, как яркие представители гордоновской школы, считают, что линейчатая поверхность должна содержать только действительные прямые. Поэтому, признавая, что линейчатая поверхность однозначно определяется тремя направляющими, добавляют: «Произвольно можно задавать только две направляющие, форма и положение третьей направляющей выбирается так, чтобы она находилась внутри конгруэнции прямых, определяемой двумя уже взятыми направляющими (С.А. Фролов). А. Л. Хейфец это условие, как я теперь понял, называет «проверкой на конгруэнтность».

С позиций теории конгруэнций этому условию отвечают конгруэнции первого порядка и k- класса Кг (1, k) (читателя, не знакомого с теорией конгруэнций, следовало бы отослать к многотомному труду классика линейчатой геометрии Рудольфа Штурма). Но он там обязательно «утонет». Поэтому я нескромно посоветую посмотреть 5-ю главу моего учебного пособия «Теоретические основы начертательной геометрии», написанного по материалам лекций на ФПКП МАИ, прочитанных в 1977 – 1990 гг. В этом случае через любую точку третьей направляющей обязательно будет проходить одна действительная образующая конструируемой линейчатой поверхности. Но загвоздка в том, что фокальными (сингулярными) линиями такой конгруэнции будут прямая a и пространственная кривая k-го порядка, для которой прямая a является (k-1) – секантой (проф. А.Л. Хейфец опять обвинит меня в наукообразии). Этот факт не согласуется с ошибочным утверждением Сергея Аркадьевича и Александра Львовича о произвольном задании первых двух направляющих для получения линейчатой поверхности только с действительными образующими.

Однополостный гиперболоид получается из конгруэнции Кг (1, 1), поэтому имеем великолепную анимацию. Торсовая поверхность образуется из конгруэнции бисекант, но она не относится к косым цилиндрическим поверхностям, поэтому их красивая анимация «не работает» на автора доклада.

Когда мы, представители четверухинской школы, говорим, что линейчатая поверхность однозначно задается любыми тремя направляющими, имеем в виду, что она содержит как действительные, так и мнимые образующие. Проф. А.Л. Хейфец, выполняя «проверку на конгруэнтность», получает не множество вариантов поверхностей косого цилиндра, а некоторые отсеки (листы) одной (!!!) поверхности, состоящие только из действительных образующих. В этом заключается его ошибка и, как следствие, наши разногласия.

Г.С. Иванов   

Уважаемый Александр Владиславович!

Большое спасибо за комментарий к нашему спору с Александром Львовичем и за добрый совет о терпимости. См. мой ответ на последний комментарий А.Л. Хейфеца. Там я объясняю суть наших разногласий.

Г.С. Иванов

Александр Львович!

Вы, отвечая на мои замечания по Вашему докладу, проявили недюжинную изворотливость в выборе места размещения ответа, а также его содержания с целью отрицания допущенного Вами очевидного геометрического «ляпа». Ваши слова «При одних и тех же направляющих возможно множество вариантов поверхностей косого цилиндра» равносильны отрицанию известного даже первокурсникам технических вузов факта, что линейчатая поверхность однозначно определяется заданием трех направляющих.

Кстати, проф. А. Л. Хейфец, Вы даже в этом небольшом по объему ответе проявили свои «геометрические способности»: «Мне было достаточно проверки на конгруэнтность». По – видимому, Вы хотели сказать «на коллинеарность».

Г.С. Иванов

Александр Львович!

Ваш доклад хорошо иллюстрирует возможности 3D анимации при изучении ряда вопросов курса начертательной геометрии, в частности, образование сложных поверхностей. Хотя тема не нова (я лично увидел подобную анимацию в 2002 году в Киеве на 10-ой конференции ISGG), но остается актуальной.

К сожалению, доклад не лишен

– небрежностей в изложении геометрических вопросов (при построении ребра возврата торса в виде линии пересечения «сферы и кругового конуса … следует решать задачу на пересечение указанных тел» (?), «цилиндр с тремя криволинейными направляющими» и др.

- ошибки («при одних и тех же направляющих возможно множество вариантов (выделено мною) поверхностей косого цилиндра»).

Эти поверхности многолистны: если направляющими a, b, c линейчатой поверхности ß являются алгебраические кривые соответственно порядков n₁, n₂, n₃, то сама поверхность ß будет порядка N = 2n₁n₂n₃, а ее направляющие a, b, c будут на ней соответственно n₂n₃-, n₁n₃-, n₁n₂- кратными, т.е. через a проходят n₂n₃ листов (пол), через b – n₁n₃ листов, а через c – n₁n₂ листов. Эти листы могут быть действительными и мнимыми. Так что вы построили несколько отсеков одной и той же (!) поверхности ß.

Кстати, на это обстоятельство я обратил Ваше внимание еще в 2008 году на конференции в МГИУ (там Вы, кажется, рассматривали цилиндроиды).

Г.С. Иванов

Уважаемые Эдуард Владимирович, Любовь Александровна, Надежда Васильевна!

Содержание Вашей статьи выпукло отражает состояние и противоречия в преподавании начертательной геометрии в настоящее время.

С одной стороны, имеем заметное снижение научно-методического уровня ее преподавания. (моя трудовая деятельность на кафедре графики началась в 1962 - ом году – после окончания института, поэтому мой опыт и стаж позволяют судить об этом профессионально). В частности, рецензируемая статья по своему научному уровню далека от аналогичной статьи Е.А. Глазунова «О проекции линии пересечения двух поверхностей второго порядка, имеющих общую плоскость симметрии» /Труды Московского семинара по начертательной геометрии и инженерной графике, М., Советская наука, 1958. С. 35 - 69.

С другой стороны, надеяться на повышение уровня знаний студентов простым (механическим) использованием компьютеров в решении задач НГ без соответствующего геометрического обеспечения, не приходится. Например, пусть рассматриваемые в статье поверхности имеют точку касания. Она на линии их пересечения может быть узловой, возврата и изолированной. Если на изображении узловую точку и точку возврата можно отличить, то как быть с изолированной точкой?

Еще один, с моей точки зрения, убедительный пример: даны две конические поверхности второго порядка с общей вершиной, их направляющие a и b принадлежат одной плоскости. Четыре их точки пересечения могут быть действительными и различными, мнимыми и совпадать в различных комбинациях! Соответственными будут вид и взаимное положение образующих, по которым пересекаются эти конические поверхности. Как быть в этом случае? Эта простая на первый взгляд задача имеет прикладное значение: двумерный гладкий обвод из отсеков рассматриваемых конических поверхностей с двумя, тремя и четырьмя совпавшими образующими можно использовать наподобие известных поверхностей Кунса для аппроксимации технических форм различного назначения. С этим же вопросом перекликаются статьи А.Г. Гирша, В.А. Короткого, опубликованные в материалах этой конференции.

Эти противоречия не являются непреодолимыми: они лишь отражают проявление «болезни роста». В идеале проблема заключается в обеспечении максимально возможного вклада начертательной (инженерной) геометрии для достижения необходимого уровня геометрической подготовки студентов с целью успешного освоения материалов последующих курсов, начиная от смежных разделов высшей математики и заканчивая курсом математического моделирования для магистров.

С уважением Г.С. Иванов

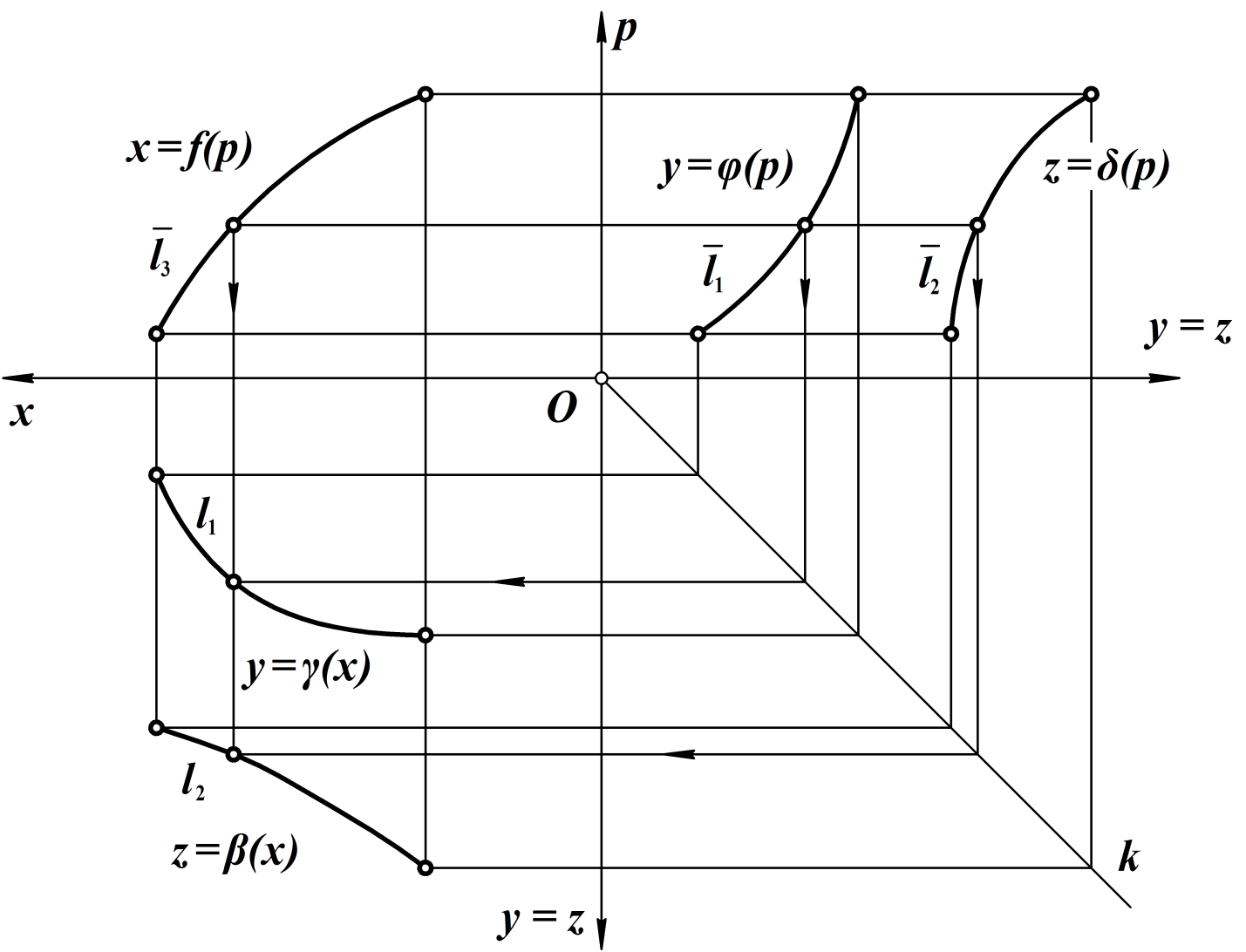
Я в своем ответе Людмиле Анатольевне говорил о тренде начертательной геометрии в инженерную в современных условиях преподавания нашей дисциплины. На Ваши замечания «НГ там отдыхает» (Л. А.), «… начертательной геометрии вообще нигде нет, кроме учебного процесса кафедр графики» (А. Л.), отвечу конкретным примером.

В компьютерной графике, САПР пространственные кривые линии задаются в параметрической форме

, , , (1)

удобной для вычислений. Но графики этих функций не позволяют строить касательные, круги кривизны. Поэтому возникает необходимость их перезадания в явной форме

y = (x), z = ß (x).     (2)

Как это делается, показано на рисунке.

Здесь дуга кривой l (1) четырехмерного пространства Oxyzp задана своими проекциями , , на обобщенном чертеже Монжа. Известными студентам 1-го курса построениями она перезадана в явной форме (2), то есть своими проекциями l₁ и l₂ на плоскостях проекций П₁(Oxy), П₂(Oxz) в трехмерном пространстве.

Дорогие оппоненты, не начертательная геометрия (тем более, инженерная геометрия) «отдыхает» в компьютерной графике, а Вы отдыхаете от начертательной геометрии! Извините за резкость (каков привет – таков ответ!)

Далее, несколько слов хочу адресовать проф. Хейфецу А.Л. Судя по Вашим публикациям, Вы под начертательной геометрией подразумеваете чертеж Монжа (2D – модель), ратуете за широкое применение 3D – моделей, аналогов аксонометрии и линейной перспективы. К Вашему сведению, эти три вида наиболее широко применяемых в практике изображений получаются по единой схеме классического метода двух изображений (см. О.А. Вольберг «Лекции по начертательной геометрии», учпедгиз, М-Л., 1947, гл. 3). Поэтому они принципиально ничем не отличаются, а отличаются лишь формой представления (изображения) объекта. Их противопоставление – это непонимание предмета линейной начертательной геометрии. Есть еще много обобщений на предмет получения нелинейных начертательных геометрий, стыкующихся с бирациональной (алгебраической) геометрией. Может быть слышали, например, о перцептивной перспективе?

Мой Вам добрый совет: не бросайтесь такими фразами «… начертательной геометрии вообще нигде нет …». Для таких заявлений следует владеть предметом разговора хотя бы в объеме кандидатского экзамена по специальности 05.01.01 (инженерная геометрия и компьютерная графика).

Г.С. Иванов

Уважаемая Людмила Анатольевна!

Кратко отвечу по п.п. 1 и 2 Вашего комментария.

1. 50-70 г.г. прошлого века были годами расцвета начертательной геометрии в СССР. Это – заслуга наших выдающихся учителей Н.Ф. Четверухина, И.И. Котова, их соратников и учеников (в том числе и И. М. Халдеева)[3]. Называть достижения и научные результаты этих лет «наукообразными», говоря очень мягко, некорректно и непрофессионально.

Значимость компьютерной графики все прекрасно понимают. Только некоторые, по-видимому, забыли, что в основе алгоритмов графических программ, наряду с достижениями электроники, лежит геометрия, в том числе, начертательная, а также смежные разделы математики. Поэтому говорить о целесообразности передачи учебных часов, отведенных начертательной геометрии, изучению компьютерной графики, равносильно предложению рубить сук, на котором сидим.

2. О необходимости изменений в преподавании начертательной геометрии начали говорить наши учителя еще в 60-70 годы прошлого века [3]. Они, будучи специалистами (подчеркнуто нами) в области прикладной геометрии и инженерной графики (инженерной геометрии и компьютерной графики), прекрасно понимали тренд трансформации начертательной геометрии в прикладную (инженерную). Отвлечемся от многомерных задач оптимизации параметров конструкций, технологических процессов и т.д. Какая кафедра и в пределах какой дисциплины может обеспечить студентов необходимым объемом знаний для освоения САПР? Проектирование одномерных и двумерных составных форм (обводов), твердотельное моделирование и т.д. требуют определенного объема знаний по теории изображений, кривых линий и поверхностей, геометрических преобразований и т.д., составляющих предмет дисциплины «инженерная геометрия».

Наверное, можно подготовить «пользователей», способных использовать те или иные графические пакеты для решения определенного круга задач. Хотелось бы только, чтобы наши инженеры были не только пользователями, но и грамотными разработчиками.

Поэтому лично меня мало утешает лозунг : «Но движемся же!»

С ув. Г.С. Иванов

Уважаемые Александр Владиславович и Людмила Анатольевна!

Благодарим за вопросы и комментарии к нашей статье.

Ваш вопрос: «Действительно ли необходима четырехмерная геометрия в техническом вузе?»

На данном этапе (!) речь идет не о преподавании начертательной геометрии многомерного пространства, а о целесообразности введения понятия многомерного пространства (число независимых точек, задающих линейную форму; формулы для подсчета размерностей объемлющего пространства и пространства пересечения p- и q- плоскостей; обобщение кинематического способа образования поверхностей хотя бы на четырехмерное пространство). Это необходимо для объяснения геометрического смысла вопросов решения систем линейных уравнений; понятий частных производных; определенных интегралов от функций трех и более переменных, а также других разделов курса высшей математики (задачи линейного, геометрического и др. программирований).

Наш опыт работы со студентами первого курса по линии НИРС по установлению межпредметных связей геометрии и линейной алгебры подтверждает реальность наших предложений.

В перспективе (!) вопреки заявлениям некоторых радикалов «о начертательной геометрии – как умирающей науке», речь идет о трансформации начертательной геометрии в инженерную. [3].

Проблема видится в другом: готовы ли преподаватели кафедр инженерной графики воплотить эту идею в жизнь? Представляется, что для этого надо проводить системную работу по повышению квалификации кадров.