Здравствуйте, уважаемые Олег Георгиевич и Дмитрий Николаевич! Спасибо за доклад. Я тоже стою на позиции, что в области геометро-графического образования умение решать задачи, а не нажимать на кнопки - важнее. И мне интересны исследования по теории геомерических построений и решению конструктивных задач. У меня по докладу одно замечание - вы не упоминаете в списке литературы книгу В.В.Глоговского "Элементарные конструктивные задачи по начертательной геометрии". Львов, 1981.

С уважением, А.Бойков

Здравствуйте, Яна! Спасибо за высокую оценку.

С уважением, А.Бойков

Здравствуйте, уважаемый Антон Георгиевич, спасибо за интересный доклад, как всегда, посвященный непростой геометрической задаче. Кроме системы построений ЦЛ (циркулем и линейкой) можно рассмотреть систему правил Фудзиты (складок оригами), которая содержит инструмент для решения уравнений третьего порядка, то есть, в принципе, может помочь в нахождении осей эллипосида. Кроме того, взяв за основу возможность пересечения пары коник (уравнение 4 порядка) можно выйти на красивые решения других сложных задач.

С уважением, А.Бойков.

Уважаемые Владимир Игоревич, Елена Владимировна и Николай Андреевич! Спасибо за доклад о геометрических местах и память о замечательном учителе. Очень рад, что работа продолжается (помню фрагменты этого исследования на семинаре "Геометрия и графика"), последовательно и всесторонне исследуются новые геометрические места. Эти знания очень полезны при подготовке к олимпиадам и, в целом, при отработке методики решения конструктивных задач.

С уважением, А.Бойков

Здравствуйте, уважаемый Виктор Алексеевич и Мария Арнольдовна! Спасибо за доклад. Ловлю себя на мысли, что в последнее время Ваш, Виктор Алексеевич, термин "визуально-образный геометрический язык" все чаще приходит на ум в контексте преподавания графических дисциплин.

С уважением, А.Бойков.

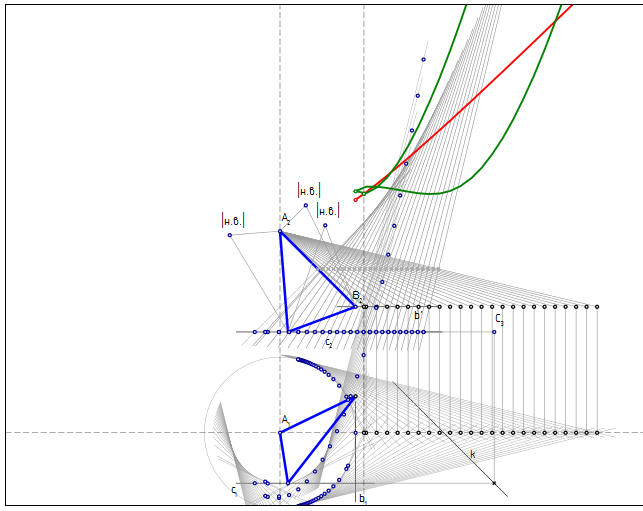
Здравствуйте, уважаемый Николай Андреевич. Спасибо за интересную статью и нелишнее напоминание об учителях! Хороший пример тому, что никакой "последний" раз в науке не может быть действительно последним, - сходство тем многих выступлений на КГП с темами статей сборника "Начертательная геометрия и инженерная графика" (1973-1990).

Насчет предложенной задачи. Во-первых, простой подсчет параметров показывает, что в случае, когда заданы только три проекции A1, B2 и C3, решений имеется ∞¹. Для этого не нужен SolidWorks. Число параметров произвольного тр-ка - 9 (∞⁹=∞³*∞³*∞³), из них 3 - формы. У равностороннего - всего один параметр формы, всего - 7. Закрепление вершины на какой-либо прямой отнимает 2 параметра, получаем ∞⁷/(∞²*∞²*∞²)=∞¹. Таким образом, для того, чтобы задача стала определенной, необходимо либо закрепить одну из точек, либо задать длину стороны. Рассмотрим первый случай. Даны три проецирующие прямые a⊥П1, b⊥П2, c⊥П3, на которых лежат точки A, B и C, соответственно. Зафиксируем точку A.

Инженерное решение 1.

Будем перемещать точку B по прямой b и поворачивать вокруг a таким образом, чтобы AB оставалась параллельна П2. При этом проекция b2 превращается в горизонтальную прямую b' (см. рис). A2B2 - натуральная величина стороны AB, а B'2 ползет по b' вправо от начального положения. Будем строить равнобедренный треугольник с основанием AB и вершиной C на c (задача для 1 курса), так как AB||П2, легко построить срединную плоскость и отсечь на c2, которая при поворотах остается неизменной, положение проекции C'2 и найти C'1 на предварительно повернутой проекции c'1. Определим длину стороны AC=BC. Будем откладывать вверх от текущего положения B'2 на b' длину AB и длину AC и получим диаграммы длин сторон - красная для AB и зеленая для AC (две ветви соответствуют повороту по часовой и против часовой стрелки). Там, где кривые пересекутся, - равнобедренный тр-к ABC становится равносторонним. Таких точек 4. Они дают положение повернутых точек B' и C', которые затем остается вернуть на основной чертеж. Поскольку построение и пересечение таких кривых может быть выполнено современным компьютером с наперед заданной точностью, найденные решения ничем не уступают полученному Александром Львовичем. Кроме того, данный способ показывает, что решений точно четыре, и дает кривые зависимости длин. На рисунке показан один из четырех тр-ков.

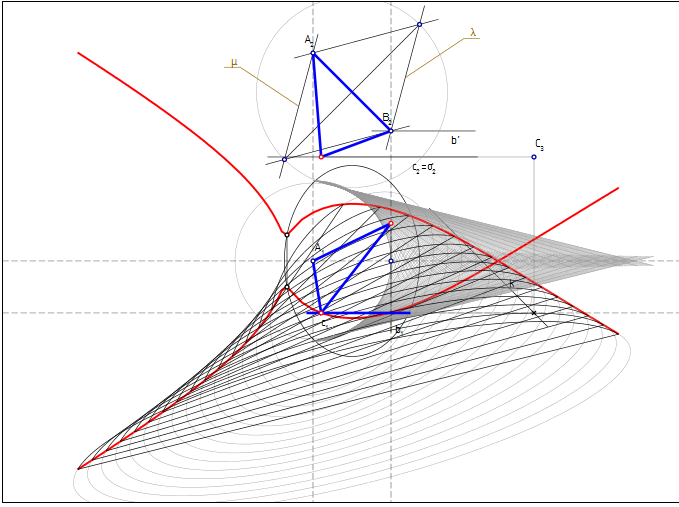
Инженерное решение 2.

Как и в предыдущем случае, будем перемещать B по b. Рассмотрим геометрическое место равносторонних треугольников со стороной AB. Это - пара круговых конусов λ и μ с углом 120 при вершине и общим основанием, расположенным в срединной плоскости AB. Геометрическое место вершин - окружность общего основания конусов. При движении B по b эта окружность изменяется, описывая циклическую поверхность, которая состоит из двух пересекающихся симметричных полостей. Пересечение ее с прямой c дает искомые вершины C. Построим сечение циклической поверхности плоскостью σ||П1 (на рис. показано красной линией, для наглядности показан также разрез образующих поверхности плоскостью σ), проведенной через c. Найдем искомые точки в пересечении полученной фигуры с c1. Их тоже четыре. Как и в предыдущем случае, компьютерная система дает возможность выполнить построение с наперед заданной точностью. Оно не уступает решению, полученному "кнопочным" способом в SolidWorks, но показывает не только число решений, но также и позволяет построить соотв.циклическую поверхность (выполнить экспорт в трехмерный пакет?) и исследовать ее свойства.

Оба решения названы инженерными, поскольку выполнены не "научными" инструментами - циркулем и линейкой, как в способе Виктора Анатольевича, а при помощи лекальных кривых. Тем не менее, если мы говорим об образовательной задаче, такое решение для студента более полезно, чем кнопочное.

С уважением, А.Бойков

Александр Олегович, спасибо за добрые пожелания! Что касается "академического начала" - если отказываться от него совсем, не придем ли мы к тому, что уже в школе начнем давать не геометрию, в целом, а моделирование штуцеров и фланцев?!

С уважением, А.Бойков

Здравствуйте, уважаемый Денис Вячеславович! Цикл докладов на КГП-2017 производит колоссальное впечатление, спасибо! Думаю после этого "Симплекс" заинтересует многих, даже тех, кто раньше, видя лишь плоские чертежи, представлял его себе как бесконечные точечные ряды и пучки прямых и окружностей. Если бы я уже не знал про него, точно бы захотел познакомиться. А учитывая примеры импорта созданных в нем кривых и поверхностей, можно надеяться, что и "Компас" пойдет на сближение. Это было бы просто отлично!

с уважением и пожеланиями успеха, А. Бойков

Здравствуйте, уважаемый Виталий Владиславович! Спасибо за интересный доклад. Мы у себя тоже занимаемся разработкой компьютерных модулей, демонстрирующих связь между чертежом и пространственной моделью, так что эта тема мне близка.

Я знаю, что у Вас имеется ряд разработок, посвященных компьютерной проверке решений задач на построение комплексного чертежа. Подскажите, на каком этапе сейчас находятся эти разработки, и к каким выводам о полезности или бесполезности такого подхода Вы пришли?

С уважением, А.Бойков

Здравствуйте, уважаемый Александр Владиславович! Спасибо за внимание к докладам и положительную оценку. К сожалению, раньше "доложиться" не мог. Насчет гиперэпюра - один из вариантов его используется в ключевом методе моделирования отсеков технических поверхностей. Но это не факторный анализ. Навскидку не приведу. Достоинство гиперэпюров, на мой взгляд, заключается в их доступности для понимания. Но это 4-5 измерений, если их 100 - совсем другой случай.

Отдльное спасибо за напоминание в Вашем докладе об организации символьных вычислений. Мысль о том, что это практически возможно сейчас при разработке любой системы, не дает мне покоя.

с уважением, А.Бойков

Здравствуйте, уважаемый Алексей Алексеевич! Спасибо за внимание к дакладу и теплые пожелания. Отвечаю на вопросы:

1. В некоторых трудах я встречал также термин "центральная аксонометрия" в обозначении перспективы. Хотя Вы совершенно правы, не стоит плодить сущностей. На сегодняшний день термин устоялся и параллельная аксонометрия звучит как "масло масляное". Спасибо за замечание.

2. Я стою на позиции, что чертеж - многофункциональный инструмент для решения научных и прикладных задач. В своем докладе Никифоров П.В. "внезапно" показал прикладное значение мнимых точек. Использование 4D для создания технических поверхностей демонстрировалось неоднократно. С другой стороны развертывание четырехмерных поверхностей - это такая "шахматная" задачка, решенная мною в качестве контрпримера к докладу Соколовой Л.С.

3. Самое прямое. Моя дипломная работа в 2004 году была посвящена кластерному анализу многомерных выборок данных. Хотя методы, используемые традиционно в многомерном статистическом анализе, кажется, далеки от НГ, но вот главные компоненты - особым образом построенная косоугольная проекция.

с уважением, А.Бойков

Здравствуйте, уважаемая Яна Андреевна! Спасибо за доклад. Рад приветствовать на КГП. Будет интересно увидеть продолжение работы и примеры использования поверхностей. Успехов! Отдельное спасибо за второй доклад по украинской школе. С удовольствием бы познакомился с трудами последних десятилетий, недоступными у нас.

С уважением, А.Бойков.

Здравствуйте, уважаемые Дмитрий Евгеньевич и Сергей Николаевич! Спасибо за интересный доклад. Как всегда, воодушевляет на поиск нового в работе со студентами. К сожалению, принтера у нас нет и пока не предвидится. Но мысль бродит, может быть что и придумается.

С уважением, А.Бойков.

Здравствуйте, уважаемый Петр Владимирович! Спасибо за этот и второй Ваш доклад. Было интересно как с точки зрения изучения возможностей "Компаса", так и с точки зрения применения системы "Симплекс" и конструктивной геометрии в целом. Считаю появление примеров совместного использования отечественных "Компаса" и "Симплекса" добрым знаком.

С уважением, А.Бойков

Здравствуйте, уважаемые Александр Олегович и Михаил Николаевич! Спасибо за интересный доклад. Согласен с Вашими тезисами. "Академическая обобщенность" не плоха сама по себе, но в сложившихся обстоятельствах невыгодна. Работая на невыпускающей кафедре со студентами первого курса (не имея соответствующего промышленного заказа) с задачниками, далекими от прикладной конкретики (об этом тоже упоминалось на прошлой конференции), невольно ловишь себя на мысли, что выиграть борьбу за "мотивацию, заинтересованность учащегося" иногда просто невозможно.

С уважением, А.Бойков

Здравствуйте, Дмитрий Евгеньевич! Спасибо за высокую оценку. Я был где-то здесь. Действительно, занят диссертацией и еще студенческой конференцией "Энергия-2017", которую в этом году добровольно-принудительно поручили мне. Насчет доклада 1 противорчеия, скорее, на уровне введения и названия. При пристальном чтении его, я заподозрил истинные причины проблемы - "мы сталкиваемся с постоянным сокращением времени", "мы вынуждены работать в режиме нарастающей интенсификации", "сколько времени уходит на то, чтобы студенты вспомнили и перечислили свойства квадрата" и др., не имеющие, строго говоря, отношения к "формальной логике и алгоритмам". Настоящий доклад для меня - попытка разобраться "с холодной головой".

С уважением, А.Бойков