Уважаемые авторы Алексей Александрович и Дмитрий Алексеевич, замутили Вы, однако, тему. Пока ничего определённого сказать не могу кроме того, что непривычно. Вы разрушаете картину целостной фигуры тем, что разлагаете её по параметрам, которыми в дальнейшем варьируете. Т.е. вообразить геометрию фигуры невозможно, возможно только следить за логикой. Есть вопрос: что такое окружность с комплексным радиусом? Может ли она появиться в результате какой-либо геометрической операции? Это двумерная фигура или трёхмерная?
С уважением, Антон Г. Гирш.

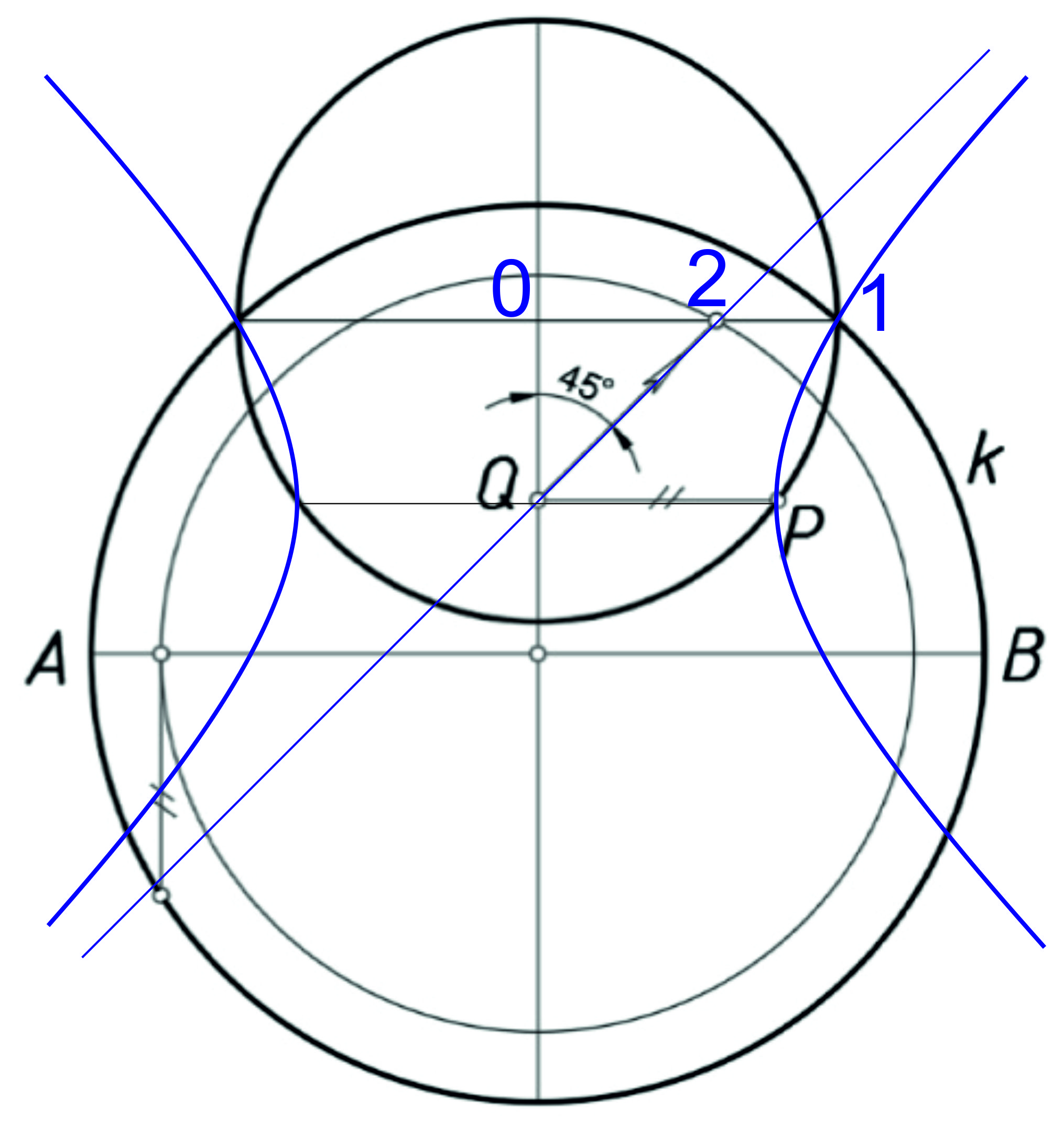
Доказательство построения через точку Р двух окружностей.

1. Равнобочная гипербола обладает свойством, что длина её полухорды (01), параллельной действительной оси (полуось QР), равна отрезку 0Р от точки 0 хорды до точки Р полуоси, 01=0Р. Это можно проверить на гиперболе x² - y²=QP². Если QP=1, Q0=2, то => 01²=5, 0P²=5.

2. Если будет известна точка 1 гиперболы, лежащая на окружности k, то определяется и точка 0 центра окружности, проходящей через току Р.

3. Но гипербола лекальная кривая и в построениях она не желательна, потому делается переход к её асимптотам. Для этого окружность k уменьшается на касательную величину QР и отмечается точка 2 пересечения этой вспомогательной окружности с асимптотой. Строится полухорде 021. Проводится окружность (0, 01), которая проходит через точку Р.

Задача решена. Задача имеет два решения. Вторая асимптота пересечёт вспомогательную окружность в точке 3. Через точку 3 проводят хорду до пересечения с осью в точке 4 и с окружностью k в точке 5. Вторая окружность (4, 45).

Схема решения:
1. Окружность (АВ) уменьшить на касательную величину РQ. Отрезок РQ имеет две засечки.
2. Из точки Q под углом 45` к диаметру провести луч до пересечения со вспомогательной окружностью.
3. Через полученную точку параллельно диаметру АВ провести хорду окружности АВ.

Доказать, что окружность, имеющая хорду своим диаметром, проходит через данную точку Р.

Литература, п.5 на с.67 задача 5.4 имеет "школьное" решение. А предложенное решение интересное и подтверждает тебя как "любителя решения сложных задач". Я тоже с этой задачкой помучился.
С уважением, Антон Г. Гирш.

Спасибо за поддержку, Николай Андреевич. Думаю, что дилема "что мы теряем и что мы выигрываем" от машинной графики ещё долго будет дискутироваться на наших форумах. На самом деле мы теряем и выигрываем. Выигрываем быстрое, скажем эскизное решение, теряем в потребности корректного решения. Неужели нас к этому склоняет технический прогресс?
С уважением, Антон Г. Гирш.

Да, конечно, потому Косте послал решение экстра письмом. Успехов в поиске точного решения. С этим точным решением мы, Виктор Анатольевич, выпадаем в осадок! Коллега решил задачку графической программой за 1 минуту.
С уважением, Антон Г. Гирш.

Спасибо за труды, Константин Григорьевич. Хотел сбросить картинку в личку, а там принимают только текст. Здесь покажу чуть позже. С уважением, Антон Г. Гирш.

Почему подвох, Константин Григорьевич? Задача не ахти какая, для разминки, но задача имеет точное решение. Решений действительно два. А вы действительно построили эти окружности или только теоретически?  Диаметр окружности, проходящей через точку Р, д.б. хордой данной окружности, хордой, параллельной АВ. Это условие для определённости. По желанию могу дать адрес, где можно посмотреть точное решение.
Спасибо за интерес.

Небольшая головоломка для любителей геометрии.

Задача. Даны окружность k с диаметром АВ и точка Р внутри окружности. Построить окружность c, проходящую через точку P и имеющую своим диаметром хорду окр. k, параллельную диаметру АВ. Сколько решений имеет задача.

Свойства окружностей с, не связанные с решением. Все окружности с образуют диаметральный пучок, имеющий огибающий эллипс с осями АВ и √2 АВ. Все окружности пучка своими мнимыми продолжениями проходят через точки А и В.

Уважаемый Александр Львович, Вы утверждаете, что нет пророка в своём отечестве! Для начала, слово "решил" имеет несколько смыслов, и как нашёл идею решения, и как исполнил построение. В последнем случае могут быть разные пути исполнения решения. Задача 9-и точек имеет с десяток разных решений. Ну и что, что В.А. Короткий говорит, что взял решение у K. Rohn и E. Papperitz. Что он у них мог взять? Скорее, идею решения, а исполнение провёл 1) по собственным алгоритмам, 2) с применением коникографа, 3) с использованием 3D-программы. То я и сказал: решил современным способом. Разве не приятно, что в наших рядах есть талантливые и трудолюбивые коллеги? Очень уж сурово Вы судите, Александр Львович.

С уважением. Антон Г. Гирш.

1) Александр Владиславович, для сферы не стоит задача нахождения трёх главных осей!

2) Александр Львович, да, когда писал в ГиГ, то не провёл основательного литературного поиска. Подсказку получил от Виктора Анатольевича, а потом, да потом, посыпалось. Похоже было, что каждый, считавший себя геометром в 19 в. приложился к этой задаче. Решений много и разнообразных, не все приемлемы на сегодня. Решил ли В.А. Короткий задачу построения ПВП по её девяти точкам? Да, решил. Современным методом.

3) Не хочу быть участником полемики "что было первично - яйцо или курица?". Машинная графика нужна, но и геометрию никто не отменял. Компьютер - инструмент, помощник, а решение задачи происходит в голове, в которой должно быть пространственное геометрическое представление. Обе спорящие стороны правы, война о том "с какого конца начинать чистить яйцо".

4) Виктор Анатольевич, Вы предложили корректное и исчерпывающее решение классической фундаментальной задачи прикладной геометрии. Приятное достижение.

С уважением. Антон Г. Гирш.

Александр Владиславович, да что это Вы так переоцениваете циркуль и линейку. Анахронизм какой-то. Уверен, что не у каждого студента есть тот циркуль. А этот пример с девятью точками поверхности второго порядка как раз и подтверждает пользу 3Д компьютерной графики и видимо в пользу сторонников последней. По поводу сферы, по точкам которой воссоздавалась бы поверхность, Вы хорошо подметили, сам такое практикую в частности окружность как коника.
С уважением, А.Г. Гирш.

Дорогой Геннадий Сергеевич, спасиб за интерес. Отправной посыл Е-геометрии - это то, что в ней принципиально могут быть только действительные фигуры. А как быть с мнимыми расширениями действительных фигур или паче того с чисто мнимыми? Они есть, они имеют форму, они имеют свойства, причём, далёкие от свойств евклидовых фигур. Да, естественно, определяются и сопоставляются свойства фигур обеих геометрий. На неполное соответствие названия плоскости для мнимых фигур указывает и В.А. Короткий. Это теоретический вопрос, над ним можно думать, а тем временем накапливаются конкретные примеры по недействительным геометрическим образам, которые и приведены в докладе. То, что линейная мера обеих геометрий параболическая, есть хорошее подспорье в построениях. Если подход выдержит тест, то доклад может стать основой для статьи, где всё и будет учтено.
С уважением. Антон Г. Гирш.

Вопросы, на которые доклад даёт ответы.

1. Что такое отрезок мнимой прямой; как определяется истинная длина отрезка; какое значение имеет истинная длина - действительное или мнимое?
2. Что такое проекция отрезка; как связана проекция отрезка со своей истинной длиной?
3. Что такое мнимый угол; как выглядит мнимый прямой угол; может ли мнимый угол иметь биссектрису; если да, то как строится биссектриса мнимого угла?

Спасибо, Александр Владиславович.

Ассоциация по примеру 1 связана с каплей. Каждая капля падая на поверхность воды выбивает в на ней кольцевую волну в виде валика, подскакивает и на мгновение зависает над водой в виде шарика. Поэты сравнивают это с серебряным гвоздиком. Такая картинка уже гуляет по интернету. Мне она напоминает открытый тор с изолированной точкой над ним. Математические поиски показали, что над поверхностью действительно находится изолированная точка, как сказал бы Ф.М. Суворов, воображаемая.

Радиус окружности +R или -R всего лишь означает, что радиус отложен от центра вправо или влево. Но если Вы хотите получить мнимую окружность, то радиус должен нести сомножитель i, т.е. корень из -1. О Пекличе молчу, он вошёл в чужую тему и очень торопился.

Уважаемый Александр Владиславович, спасибо, что заглянули в эту статью, менее приятно примечание про "человеческую глупость". Тема то относительно новая в прикладной геометрии, термины ещё не обкатаны и не общеприняты, так что шероховатосей быть не должны, но возможны. Будем работать над ошибками.