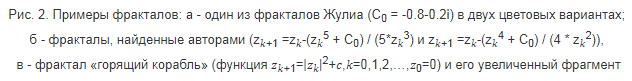Здравствуйте, Денис Вячеславович! Спасибо за высокую оценку. Ваши эксперименты в Симплексе с инверсиями относительно мнимых окружностей и статьи Антона Георгиевича не давали покоя, хотелось увидеть все эти "мнимые" фигуры. И, кажется, что-то в этом направлении стало получаться.

с уважением, А.Бойков

Александр Владиславович, спасибо за внимание к докладу и ценные замечания!

Статья В.А. Краснова в настоящий момент не доступна, обязательно почитаю.

Насчет п. 1. Самопересечение, похоже, возникает при проецировании.

Если рассматривать пересечение действительной окружности с ∞¹ пучками параллельных прямых, всякий раз получаем мнимое продолжение в виде гиперболы. То есть имеется что-то вроде гиперболоида вращения, но каждый меридиан такого гиперболоида дополнительно повернут вокруг действительной плоскости, так что при проецировании в какое-либо пространство одна из ∞¹ гипербол сжимается в пару двойных лучей, отчего возникает самопересечение.

с уважением, А.Бойков

Уважаемые организаторы конференции!

Я и мои соавторы сердечно благодарим за возможность поделиться своими результатами с уважаемыми коллегами, познакомиться с результатами их работы, за возможность "встретиться" и пообщаться, за соединяющий всех нас геометро-графический дух конференции! Мне лично очень не хватило конференции в прошлом году и я очень рад, что КГП-2019 состоялась!

С уважением, наилучшими пожеланиями и надеждой на лучшее, А.Бойков.

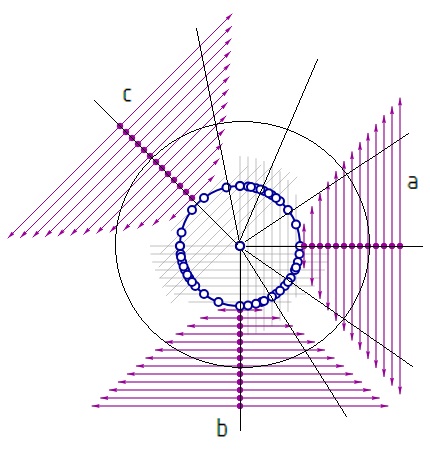
Здравствуйте, Антон Георгиевич! Спасибо за внимание к нашему докладу.

Окружность с комплексным радиусом у нас получается в общем случае, если задать ее тремя произвольными (не сопряженными) точками с комплексными координатами. Например, берем три точки:

A = [P 60 + 60i, 60 + 60i], B = [P -50 + 50i, 50 - 50i], C = [P -50i, 50i]

Вычислительная процедура, работающая по обычным формулам для действительной окружности, но с внутренней поддержкой комплексных вычислений определяет центр и радиус:

o=c3p(A,B,C)

o = [x = 25.833333333333332 + 30i, y = 75.83333333333333 + 30i, r = 19.77977285674572 + 27.806183821389418i]

При подстановке координат исходных точек в уравнение x²+y²-r²=0, получаем тождество, то есть исходные точки принадлежат такой окружности.

Для сравнения - проекция окружности с действительным (слева) и комплексным (справа) радиусом в пространство x_i-xOy:

По поводу размерности фигуры вопрос не совсем понятен. Любая линия, задаваемая уравнением типа F(x,y)=0 на комплексной плоскости, представляет собой точечное множество ∞², то есть поверхность.в обычном понимании этого слова. Поскольку каждая точка двухмерной комплексной пл-ти имеет 4 степени свободы (x, x_i, y, y_i), то двухмерная комплексная плоскость, фактически, есть 4-мерное пространство, в котором лежат эти поверхности. Причем эти поверхности, в общем случае, искривлены так, что не могут лежить ни в одном трехмерном подпространстве полностью (по аналогии с пространственными кривыми, которые "не имеют натуральной величины" на плоскости, эти - не имеют натуральной величины в трехмерном пространстве и всегда проецируются в трехмерное пространство с искажением).

с уважением, А.Бойков

Здравствуйте, Елена Петровна и Валентина Дмитриевна! В заголовке и тексте доклада перепутаны термины "геометрия" и "начертательная геометрия", в частности, в списке литературы приводятся два источника с противоположными мнениями о "начертательной геометрии". Обобщения, приведенные в заключении, относятся к "геометрии" в целом.

с уважением, А.Бойков

Здравствуйте, Олег Георгиевич! Спасибо за познавательный доклад. Как правидо, в публикациях о методах решения конструктивных задач ограничиваются задачами, не требующими для решения иных инструментов, кроме циркуля и линейки. Вы для решения задачи применяете специальные графики (диаграммы). Построение такого графика предполагается вручную, при помощи сплайна или имеется в виду какая-то автоматизация? Интересно было бы увидеть, возможно или нет решать такие задачи в системе конструктивных аксиом оригами-геометрии (правило Белок позволяет решать уравнения 3-го порядка) или такими инструментами, как пара пересекающиеся коники (в системе конструктивной геометрии Симплекс можно пересеть две кривые второго порядка или при помощи полярного преобразования построить касательные к двум коникам - то есть уравнения 4-го порядка) и др.

с уважением, А.Бойков

Здравствуйте, Денис Вячеславович и Елена Петровна! Большое спасибо за статьи, которые наверняка будут интересны не только тем, кто хочет лучше понять принципы работы "Симплекса", но и так или иначе решает задачи разработки систем конструктивной геометрии.

с уважением, А.Бойков

Здравствуйте, Дмитрий Евгеньевич, Сергей Николаевич  и Константин Олегович! Большое спасибо за подробный и содержательный анализ серьезного вопроса. Есть над чем подумать.

с уважением, А. Бойков

Здравствуйте, Татьяна Владимировна!

Спасибо за доклад. Считаю, что любой технический специалист должен уметь выражать свою геометрическую идею в эскизе.

с уважением, А.Бойков

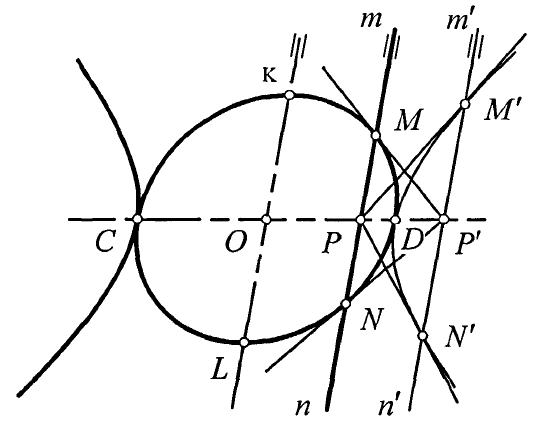
Уважаемый Антон Георгиевич! Спасибо за интересные статьи о мнимых элементах. Видел Вашу статью с описанием конструктивных задач в области мнимого в сборнике МАИ, и тогда еще у меня возник вопрос о том, как правильно применять описанные конструктивные алгоритмы при решении задач на чертеже. В докладе на рис. 1 показана обычная плоскость (координированная x-y), на рис. 2-4 мы обозначены оси координат x-i и r-i. Это немного путает. Как применять построения на обычном чертеже, координированном x-y, куда направлять мнимые x_i и y_i? Пусть, например, имеется известное построение мнимых точек пересечения коники с прямой (чтобы не придумывать, воспроизвожу чертеж из работы Понселе по дисс. О.А. Графского):

Мы знаем, что точка C и O действительные, а M' и N' - мнимые сопряженные (P' - их действительная часть). Можно как-то найти длину отрезка CM' или OM', как это правильно сделать?

Заранее благодарю.

с уважением, А.Бойков

Здравствуйте, Диана Дмитриевна, Никита Андреевич и Галина Геннадьевна! Спасибо за доклад. Тема, я считаю, актуальная и интересная. 

с уважением, А.Бойков

Здравствуйте, Александр Львович! Благодарю за прекрасно иллюстрированный доклад с решением интересной практической задачи.

с уважением, А.Бойков

Здравствуйте, Александр Владиславович! Спасибо за подробный обзор и теплые слова. Некоторые работы мне не попадались, нужно поискать. Считаю, что такие обзоры нужны и служат хорошим напоминанием о том, что уже было сделано в самых разных областях геометрии, в частности, отечественными учеными. В ИГЭУ многомерной геометрией применительно к диаграммам состояния сплавов занимался Ю.А. Малеев.

На меня памятная дискуссия на КГП-2017 произвела то же самое впечатление. И, как теперь оказалось, многомерные приложения находятся сами собой, в какую область не посмотри. В нашем докладе о фракталах появилось сначала 4-мерное, потом 5- и 6-мерное пространство. При попытках визуализовать фигуры комплексной плоскости само собой появляется 4-мерное (x+ix_i, y+iy_i) пространство, а если вслед за А.Г. Гиршем (см. доклад об изолированных точках) отправиться в комплексное пространство, то и 6-мерное. 

с уважением, А.Бойков

Здравствуйте, Анна Анатольевна! Спасибо за внимание к статье и замечания.

Главная проблема созданных в рамках исследования программ - невозможность выбирать и корректировать цветовую гамму. Эта проблема будет решена в создаваемом редакторе. Приведенные Вами ссылки ведут на примеры геометрических, не алгебраических фракталов, хотя, несомненно, красивых.

с уважением, А.Бойков

Здравствуйте, Виталий Владиславович! Большое спасибо за внимание к статье и высокую оценку. В ИГЭУ фрактальные алгоритмы бегло рассматриваются на факультете информатики и вычислительной техники в рамках третьей части дисциплины "Инженерная и компьютерная графика" (ранее курс назывался "Алгоритмы машинной графики"), зато появляется возможность познакомиться подробнее в рамках творческих работ.

с уважением, А.Бойков

Вставляю картинкой. Подрисуночная подпись должна быть:

с уважением, А. Бойков

Здравствуйте, Александр Владиславович!

Спасибо за высокую оценку и справедливые замечания. Четвертого автора зовут Шкилевич Антон Александрович, он в 2017 году начал эту работу по систематическому построению миниатюр фракталов типа ФЖ для различных функций и фракталов типа ФМ, но в этом году в период проведения конференции не смог присоединиться к нам. Значки "...", конечно, конспирация. Мы несколько раз перерабатывали текст, вначале планировалось все формулы вписать текстом, потом решили встроить формулы в картинки, в итоге - накладка. Прошу прощения. Подрисуночная подпись должна быть:

Рис. 2. Примеры фракталов: а - один из фракталов Жулиа (C₀ = -0.8-0.2i) в двух цветовых вариантах; 
б - фракталы, найденные авторами (z

Здравствуйте, Николай Андреевич! Спасибо за теплые слова. С проективографией почти не знаком, слышал краем уха, хотя книга (почти журнал с иллюстрациями!) Гамаюнова В.Н. в личной базе в фотокопии имеется. Почитаю.

с уважением, А.Бойков

Здравствуйте, Александр Львович! Спасибо за высокую оценку доклада. Прошу прощения за поздний ответ, два дня в дороге. Попробую ответить на вопросы.

Время на построение определяется размерами картинки в пикселах (WxH) и числом итераций (K) для каждого пиксела, то есть при наихудшем исходе пропорционально ~WxHxK. Мой собственный опыт подобных программ на Delphi показывает для картинки 800x800x40 на персональном компьютере семилетнего возраста порядка 1,5-2 мин, хотя я видел примеры построения фрактала Мандельброта практически в реальном времени. Екатерина и Анастасия делали изображения в высоком разрешении - около 4тыс.пикселов на сторону и с большим числом итераций. Время формирования до 40 минут, поэтому в проекте приложения заложен пакетный режим формирования, когда запустил - и пошел спать.

Насчет создания картинки в AutoLISPе у меня встречный вопрос - позволяет ли он вообще создавать растровые картинки по пикселам? Другой тип фракталов - геометрические для чертежной программы вполне "по зубам", поскольку можно рекурсивно добавлять в модель отрезки, кружки и пр., но алгебраические фракталы, как правило, строятся по пикселам. Существуют алгоритмы, в той же книге [1], по-моему, для построения контуров множества Мандельброта или эквипотенциальных кривых. Такую картинку в AutoCADе построить можно вполне. В любом случае производительность будет низкая, поскольку AutoLISP работает в режиме интерпретатора.

с уважением, А.Бойков

Здравствуйте, Людмила Георгиевна и Тимур Рустямович! Спасибо за очень ценный доклад, на фоне грандиозных проектов с 3D-моделированием напоминающий о сути геометрического образования. Я, действительно, разделяю идеи формализации и алгоритмизации в геометрии, но относится это именно к геометрическим инструментам, предназначенным для решения практических задач. Для того, чтобы уметь сставить и применить алгоритм, геометрическое мышление даже более необходимо, чем геометрическая интуиция. В том, что касается педагогических задач геометро-графического образования, полностью поддерживаю Вашу точку зрения. Насчет "круглого стола" - идею поддерживаю. Может быть, удастся пообщаться на МГО, особенно если не придется проверять, как в прошлый раз, до 22.

с уважением, А,Бойков

Здравствуйте, Евгений Викторович! Спасибо за хороший доклад. Всегда с интересом читаю в Ваших работах о применении кусочных кривых и поверхностей, полученных на основе БН-исчисления, для решения практических задач.

с уважением, А.Бойков

Здравствуйте, Владимир Игоревич, Павел Андреевич и Ольга Владимировна! Спасибо за любопытную конструктивно-геометрическую задачу с практическим применением и ее решение. Вопрос тот же самый, что у Александра Львовича, какие возможности автоматизации построения такой "ленты" предоставляет САПР (Inventor, полагаю?) или, действительно, программирование?

с уважением, А.Бойков

Здравствуйте, Антон Георгиевич! Большое спасибо за еще один интересный и глубоко геометрический доклад. Любопытно, что построить меридианы и задать секущую плоскость, которая дает, к примеру, мнимые круги Вилларсо, значительно проще, если пользоваться чертежом, чем в любой трехмерной САПР.

с уважением, А.Бойков

Здравствуйте, Ольга Львовна! Спасибо за интересное сообщение. Для меня данная область является совершенно незнакомой и очень хорошо, что в рамках общей геометро-графической конференции можно узнать о новых областях практического применения геометрии и графики.

с уважением, А.Бойков

Уважаемые Владимир Адольфович и Иван Игоревич!

Благодарю Вас за доклад. Работа впечатляющая - масштабная задача, "фантастическая" в том смысле, что студенты-первокурсники, работая в "Компас-3D", изучая азы, часто не понимают, что "крышки", "шпиндели" и "пробки" не самоцель, и что система геометрического моделирования, - инструмент, который в умелых руках может творить чудеса. Спасибо за напоминание и яркие примеры настоящей работы!

с уважением, А.Бойков

Спасибо за высокую оценку! Планируются два доклада со студентами, но, ввиду довольно большого объема материала, дело затягивается. 

Кстати, мне кажется, было бы интересно сравнить ГиГ с другими ВАКовскими по специальности 05.01.01, как по всяким хиршам, так и по числу выпусков/статей в год, среднему объему статьи, числу ссылок и условиям (читай, стоимости) публикации для авторов, а также проанализировать динамику их показателей. В том числе и тех, кто по каким-то причинам "сошел" с дистанции.

с уважением, А.Бойков

Уважаемые Владимир Игоревич и Николай Андреевич! Спасибо за обстоятельный анализ, и за работу над журналом, разумеется! Кроме вышеперечисленного в докладе хочу отметить уникальность "ГиГ"а - как единственного чисто "геометрического" ВАКовского журнала. Для сравнения - "Вестник компьютерных и информационных технологий" - скорее, программистский. По другим не скажу, в них не публиковался. В общем, желаю журналу укрепления позиций и дальнейшего роста уровня статей, а людям, его создающим, крепкого здоровья и успехов.

с уважением, А.Бойков